精品解析：河南省郑州市第五十七中学2021-2022学年七年级上学期期末数学试题（原卷版）

这是一份精品解析：河南省郑州市第五十七中学2021-2022学年七年级上学期期末数学试题（原卷版），共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（每小题3分，共30分）
1. 在，-1，0，-3这四个数中，最小的是（ ）
A. B. －1C. 0D. －3
【答案】D
【解析】
【分析】根据比较有理数大小的方法，可得答案．
【详解】解：∵，，，
∴
∴
故最小的数是-3．
故选：D．
【点睛】本题考查了有理数比较大小，掌握正数大于0，0大于负数，两个负数比较，绝对值大的反而小是解题的关键．
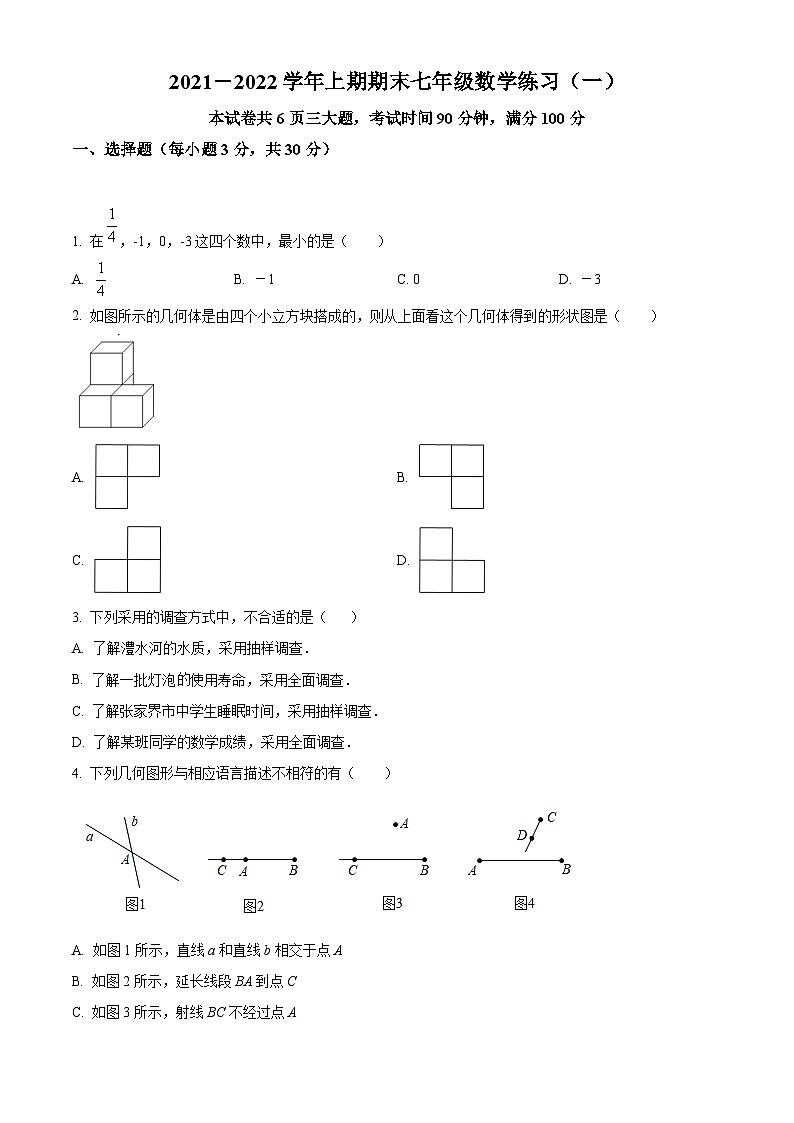
2. 如图所示的几何体是由四个小立方块搭成的，则从上面看这个几何体得到的形状图是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】根据俯视图的定义，从上往下看到的几何图形是俯视图即可判断．
【详解】解：从几何体上面看，左往右2列小正方形的个数依次为：2，1．前往后2列小正方形的个数依次为：1，2．
故选：D．
【点睛】本题考查简单组合体的三视图，理解视图的意义，掌握三视图的画法是得出正确答案的前提．
3. 下列采用的调查方式中，不合适的是（ ）
A. 了解澧水河的水质，采用抽样调查．
B. 了解一批灯泡的使用寿命，采用全面调查．
C. 了解张家界市中学生睡眠时间，采用抽样调查．
D. 了解某班同学的数学成绩，采用全面调查．
【答案】B
【解析】
【分析】根据调查对象的特点，结合普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果接近准确数值，从而可得答案．
【详解】解：了解澧水河的水质，采用普查不太可能做到，所以采用抽样调查，故A合适，
了解一批灯泡的使用寿命，不宜采用全面调查，因为调查带有破坏性，故B不合适，
了解张家界市中学生睡眠时间，工作量大，宜采用抽样调查，故C合适，
了解某班同学的数学成绩，采用全面调查．合适，故D合适，
故选B．
【点睛】本题考查的是抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．
4. 下列几何图形与相应语言描述不相符的有（ ）
A. 如图1所示，直线a和直线b相交于点A
B. 如图2所示，延长线段BA到点C
C. 如图3所示，射线BC不经过点A
D. 如图4所示，射线CD和线段AB有交点
【答案】B
【解析】
【分析】根据直线、射线、线段的相关概念可直接进行排除选项．
【详解】解：A、如图1所示，直线a和直线b相交于点A，几何图形与相应语言描述相符，故不符合题意；
B、如图2所示，延长线段BA到点C，几何图形与相应语言描述不相符，故符合题意；
C、如图3所示，射线BC不经过点A，几何图形与相应语言描述相符，故不符合题意；
D、如图4所示，射线CD和线段AB有交点，几何图形与相应语言描述相符，故不符合题意；
故选B．
【点睛】本题主要考查直线、射线与线段，熟练掌握直线、射线与线段的相关概念是解题的关键．
5. 2021年12月9日下午，“天宫课堂”第一课正式开讲．作为中国空间站的首次太空授课，神舟13号乘组航天员翟志刚、王亚平、叶光富设计了一系列精巧、直观的实验，为青少年展示微重力环境下“水球”开花、漂浮转身，浮力消失等神奇现象．据悉，首课结束仅一天，“中国空间站首次太空授课”话题播放量达到1.1亿次．其中1.1亿用科学记数法表示正确的为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】科学记数法的表现形式为的形式，其中，n为整数，确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同，当原数绝对值大于等于10时，n是正数，当原数绝对值小于1时n是负数；由此进行求解即可得到答案．
【详解】解：1.1亿=110000000=
故选：A．
【点睛】本题主要考查了科学记数法，解题的关键在于能够熟练掌握科学记数法的定义．
6. 某学校在植树节派出50名学生参与植树，统计每个人植树的棵数之后，绘制出如图所示的频数直方图（图中分组含最小值，不含最大值），则植树不足7棵的人数占总人数的（ ）
A. B. C. D.
【答案】C
【解析】
【分析】用植树不足7棵的人数和除以总人数即可．
【详解】解：由图形知，植树不足7棵的人数占总人数的百分比为×100%=24%，
故选：C．
【点睛】本题主要考查频数分布直方图，解题的关键是根据频数分布直方图得出解题所需数据．
7. 六棱柱的截面不可能是（ ）
A. 六边形B. 七边形C. 八边形D. 九边形
【答案】D
【解析】
【分析】六棱柱有八个面，截面与其八个面相交最多得八边形，不可能是九边形或多于九边的图形．
【详解】解：用平面去截六棱柱，得的截面可能为三角形、四边形、五边形、六边形、七边形、八边形，不可能为九边形，故D正确．
故选：D．
【点睛】本题主要考查六棱柱截面，六棱柱的截面的几种情况应熟记．
8. 新型冠状肺炎疫情正在全球蔓延肆虐，口罩成了人们生活中必不可少的物品．某口罩厂有26名工人，每人每天可以生产400个口罩面或500个口罩耳绳，一个口罩面需要配两个耳绳，为使每天生产的口罩刚好配套，设安排x名工人生产口罩面，则下列所列方程正确的是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】安排x名工人生产口罩面，则人生产耳绳，由一个口罩面需要配两个耳绳可知耳绳的个数是口罩面个数的2倍从而得出等量关系，就可以列出方程．
【详解】解：设安排x名工人生产口罩面，则人生产耳绳，
由题意得
．
故选：C．
【点睛】本题考查了由实际问题抽象出一元一次方程，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程．
9. 把9个数填入3×3的方格中，使其任意一行，任意一列及两条对角线上的数之和都相等，这样便构成了一个“九宫格”．它源于我国古代的“洛书”（图1），是世界上最早的“幻方”．图2是仅可以看到部分数值的“九宫格”，则其中a的值为（ ）
A. 2B. 4C. 6D. 1
【答案】D
【解析】
【分析】根据题意设左边中间位置为b，左上为c．求出“九宫格”中的b、c，再求出a即可求解．
【详解】如图，依题意可得2+5+8=3+5+b，
解得b=7．
∴2+5+8=2+7+c，
解得c=6．
∴2+5+8=6+8+a，
解得a=1．
故选：D．
【点睛】此题主要考查一元一次方程的应用，解题的关键是根据题意得到方程求解．
10. 按照如图所示的程序计算，若开始输入的值为－4，则最后输出的结果可能是（ ）
A. －8B. －23C. －68D. －32
【答案】D
【解析】
【分析】根据程序可知，输入x计算，若所得的值大于或等于﹣20，则将所得的值代入计算，直到所得的值小于﹣20即可输出．
【详解】解：当x=﹣4时，＝﹣11，
∵﹣11＞﹣20，
∴当x=﹣11时，＝﹣32，
∴当x=﹣11时，＝﹣32＜﹣20，则最后输出结果为﹣32，
故选：D．
【点睛】此题考查了程序计算，有理数混合运算，正确理解程序图计算是解题的关键．
二、填空题（每小题3分，共15分）
11. 如图，、是河两侧的两个村庄，现要在河上修建一个抽水站，使它到、两村庄的距离之和最小．老师说：连接，则线段与的交点即为抽水站的位置．其理由是：_____________________．
【答案】两点之间线段最短
【解析】
【分析】根据线段的性质，可得答案．
【详解】解：连接AB，则线段AB与l的交点C即为抽水站的位置．其理由是：两点之间线段最短．
故答案为：两点之间线段最短．
【点睛】本题考查了线段的性质，利用线段的性质是解题关键．
12. 若和的和仍是一个单项式，则ab ＝_________．
【答案】-20
【解析】
【分析】若两个单项式的和是单项式，则它们一定是同类项，根据同类项的概念得到关于a，b的方程，从而求解．
【详解】解：∵单项式与的和仍是一个单项式，
∴a＝5，2b＝3b+4，
解得：a＝5，b＝-4，
∴ab＝-20．
故答案为：-20．
【点睛】本题主要考查了同类项的概念，即含有相同字母，相同字母的指数相同的单项式叫同类项．
13. 对于两个互不相等的有理数a，b我们规定符号表示a，b两个数中最大的数，例如．按照这个规定则方程的解为______．
【答案】
【解析】
【分析】分类讨论0与−x的范围，方程利用题中的新定义变形，计算即可求出解．
【详解】解：当0>−x，即x>0时，方程变形得：0=3x+4，
解得：，不符合题意；
当0<−x，即x<0时，方程变形得：−x=3x+4，
解得：x=−1，
综上，方程的解为x=−1，
故答案为：x=−1．
【点睛】此题考查了解一元一次方程，熟练掌握运算法则是解本题关键．
14. 一家体育器材商店将某种品牌的篮球按成本价提高40%后标价，又以8折优惠卖出，仍可获利12元．若设每个篮球的成本价为a元，依据题意可列方程_________
【答案】(1+40％) a×80%-a=12
【解析】
【分析】设每个篮球的成本价为a元，然后根据题中的等量关系列方程即可．
【详解】解：设每个篮球的成本价为a元，
由题意得：（1+40%）a×80%﹣a＝12，
故答案为：(1+40％) a×80%-a=12．
【点睛】本题主要考查了一元一次方程的应用，用一元一次方程这个数学模型来解答实际问题是中考的常见题．注意：利润＝售价﹣进价．其中八折即标价的80%．
15. 如图，O为直线AB上一点，作射线OC，使．将一个直角三角板按如图1所示的方式摆放，直角顶点在点O处，一条直角边OP在射线OA上．将图1中的三角尺绕点O以每秒的速度按逆时针方向旋转（如图2所示），在旋转一周的过程中，第t秒时，OQ所在直线恰好平分，则t的值为______．
【答案】8或20
【解析】
【分析】由平角的定义可得∠BOC=60°，然后根据角平分线定义列出方程求解即可．
【详解】解：∵，
∴∠BOC=60°
∵OQ所在直线恰好平分∠BOC，
∴∠BOQ=∠BOC=30°或∠BOQ=180°+30°=210°，
∴15t=30+90或15t=90+210，解得t=8或20．
故答案为：8或20．
【点睛】本题主要考查了一元一次方程的应用，根据角平分线定义、平角的定义、列出方程是解答本题的关键．
三、解答题（本大题共7个小题，共55分）
16.
【答案】##0.5
【解析】
【分析】先计算乘方，再计算乘除，最后计算加减即可．
【详解】解：原式= = =
【点睛】本题考查有理数混合运算，熟练掌握有理数运算法则是解题的关键．
17. 先化简，再求值：，其中，．
【答案】-2x2+xy-4y2，-10
【解析】
【分析】先去括号合并得到最简结果，把的值代入计算即可求出结果．
【详解】
；
当时，
原式
．
【点睛】本题考查了整式的加减-化简求值，熟练掌握运算法则是解本题的关键．
18. 2021年4月，教育部印发《关于进一步加强中小学生睡眠管理工作的通知》，明确要求初中生每天睡眠时间应达到9小时某初级中学为了解学生睡眠时间的情况，从本校学生中随机抽取500名进行问卷调查，并将调查结果用统计图描述如下．
平均每天睡眠时间x（时）分为5组：①5≤x＜6；②6≤x＜7；③7≤x＜8；④8≤x＜9；⑤9≤x＜10，根据以上信息，解答下列问题：
（1）请补全频数分布直方图；
（2）本次调查中，认为“校外学习任务重”影响睡眠的圆心角的度数为______ ，达到9小时的学生人数占被调查人数的百分比为______ ；
（3）请对该校学生睡眠时间的情况作出评价，并提出一条合理化建议．
【答案】（1）见解析 （2）118.8° ；17％ （3）见解析
【解析】
【分析】（1）用调查总人数减去其他四组的人数得到答案，再补全频数分布直方图即可；
（2）用乘以“校外学习任务重”所占百分比即可得到答案；
（3）根据题意说出一条合理的建议即可．
【小问1详解】
解：500-20-130-180-85=85人，
补全频数分布直方图如下图：
【小问2详解】
解：由题意得：“校外学习任务重”影响睡眠的圆心角的度数为，
达到9小时的学生人数占被调查人数的百分比为，
故答案为：118.8°；17%；
【小问3详解】
解：建议：该校各学科授课老师精简家庭作业内容，师生一起提高在校学习效率；学生减少参加校外培训班，校外辅导机构严禁布置课后作业．答案不唯一，言之有理即可．
【点睛】本题主要考查了扇形统计图和条形统计图，求扇形统计图圆心角度数，求条形统计图相关数据等等，正确读懂统计图是解题的关键．
19. 给定方程，联系生活实际编写一道数学问题，并解答该问题．
【答案】我今年的年龄是12岁，爸爸的年龄是40岁，请问：几年以后爸爸的年龄是我年龄的3倍？2年以后爸爸的年龄是我年龄的3倍
【解析】
【分析】根据所给方程联系生活实际编写应用题，注意等量关系，处理好3倍关系即可
【详解】举例：我今年的年龄是12岁，爸爸的年龄是40岁，请问：几年以后爸爸的年龄是我年龄的3倍？
解：设x年后爸爸的年龄是我年龄的3倍．
由题可知．
解得：．
答：2年以后爸爸的年龄是我年龄的3倍．
【点睛】本题考查了一元一次方程的应用，理解方程中的等量关系是解题的关键．
20. 下图是由边长相同的小正方形组成的，其中部分小正方形涂有阴影，依此规律完成此题
（1）a＝_____ ， b＝_____；
（2）按照这种规律继续下去，则第n个图形中涂有阴影的小正方形的个数为___________；（用含n的代数式来表示）
（3）按照这种规律继续下去，用（2）中的代数式求第2022个图形中涂有阴影的小正方形的个数．
【答案】（1）9；17
（2）4n+1 （3）8089根
【解析】
【分析】（1）观察图形规律，可知第1个小正方形阴影有5个，第2个小正方形阴影有5+4=9个，第3个小正方形阴影有5+4×2=13个，以此类推，可知第4个为5+4×3=17个；
（2）第n个为5+4（n-1）=；
（3）将代入即可．
【小问1详解】
第2个小正方形阴影有5+4=9个；
第4个小正方形阴影有5+4×3=17个
故答案为：9，17；
【小问2详解】
观察图形规律，可知：
第1个小正方形阴影有5个，
第2个小正方形阴影有5+4=9个，
第3个小正方形阴影有5+4×2=13个，
以此类推，
第n个为5+4（n-1）=；
故答案为：；
【小问3详解】
将代入中得：
即第2022个图形需要的火柴棒根数为8089根．
【点睛】本题是图形的规律探究题，找到题目中的规律，并用代数式把规律表示出来是解决本题的关键．
21. 已知OC为一条射线，OM平分∠AOC，ON平分∠BOC．
（1）如图1，当∠AOB＝60°，OC为∠AOB内部任意一条射线时，∠MON＝ ；
（2）如图2，当∠AOB＝60°，OC旋转到∠AOB的外部时，∠MON＝ ；
（3）如图3，当∠AOB＝α，OC旋转到∠AOB（∠BOC＜120°）的外部时，求∠MON，请借助图3填空．
解：因为OM平分∠AOC，ON平分∠BOC
所以∠COM＝∠AOC，∠CON＝∠BOC （依据是 ．）
所以∠MON＝∠COM－
＝∠AOC－
＝
【答案】（1）30° （2）30°
（3）角平分线的定义，，，α
【解析】
【分析】（1）根据角平分线定义可得∠MOC＝∠AOC，∠NOC＝∠BOC，再利用角的和差可得∠MON的度数；
（2）根据（1）的思路可得答案；
（3）根据角平分线的定义与角的和差可得答案．
【小问1详解】
解：∵OM平分∠AOC，ON平分∠BOC，
∴∠MOC＝∠AOC，∠NOC＝∠BOC，
∴∠MON＝∠MOC+∠NOC＝∠AOC+∠BOC＝∠AOB＝30°．
故答案为：30°；
【小问2详解】
解：∵OM平分∠AOC，ON平分∠BOC，
∴∠MOC＝∠AOC，∠NOC＝∠BOC，
∴∠MON＝∠MOC﹣∠NOC＝∠AOC﹣∠BOC＝∠AOB＝30°．
故答案为：30°；
【小问3详解】
解：∵OM平分∠AOC，ON平分∠BOC，
所以∠COM＝∠AOC，∠CON＝∠BOC（角平分线定义），
所以∠MON＝∠COM﹣∠CON，
＝∠AOC﹣∠BOC，
＝α．
故答案为：角平分线定义，∠CON，，α．
【点睛】本题考查角计算和角平分线的定义，熟练掌握角平分线的定义与角的和差是解题关键．
22. A、B两地相距，甲车的速度从A地匀速驶往B地，甲车出发30分钟后，乙车以的速度也从A地匀速驶往B地，两车相继到达终点B地，乙车行驶多长时间后，甲、乙两车恰好相距？
【答案】或
【解析】
【分析】设乙车行驶x h后，甲、乙两车恰好相距20km，分乙车追上甲车之前相距20km及乙车追上甲车之后相距20km以及乙到达终点与甲相距20km三种情况考虑，利用两车的路程之差为20km，即可得出关于x的一元一次方程，解之即可得出结论．
详解】解：设乙车行驶后，甲、乙两车恰好相距，
①当乙已经从A地出发，甲在乙前：
，
解得：；
②当乙已经从A地出发，乙在甲前：
，
解得：；
③当乙车到达终点时：
，
解得：；
乙车行驶或后，甲、乙两车恰好相距．
【点睛】本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．调查问卷
1.近两周你平均每天睡眠时间大约是______小时．
如果你平均每天睡眠时间不足9小时，请回答第2个问题
2.影响你睡眠时间的主要原因是______（单选）
A.校内课业负担重
B.校外学习任务重
C.学习效率低
D.其他
图形标号
第一个
第二个
第三个
第四个
涂有阴影的小正方形的个数
5
a
13
b