广东省河源市龙川县新田中学 2022-2023学年七年级上学期期中数学试卷

广东省河源市龙川县新田中学 2022-2023学年七年级（上）期中数学试卷

一．选择题（共10小题，满分30分，每小题3分）

1．（3分）若a与1互为相反数，那么a+1＝（　　）

A．﹣1 B．0 C．1 D．﹣2

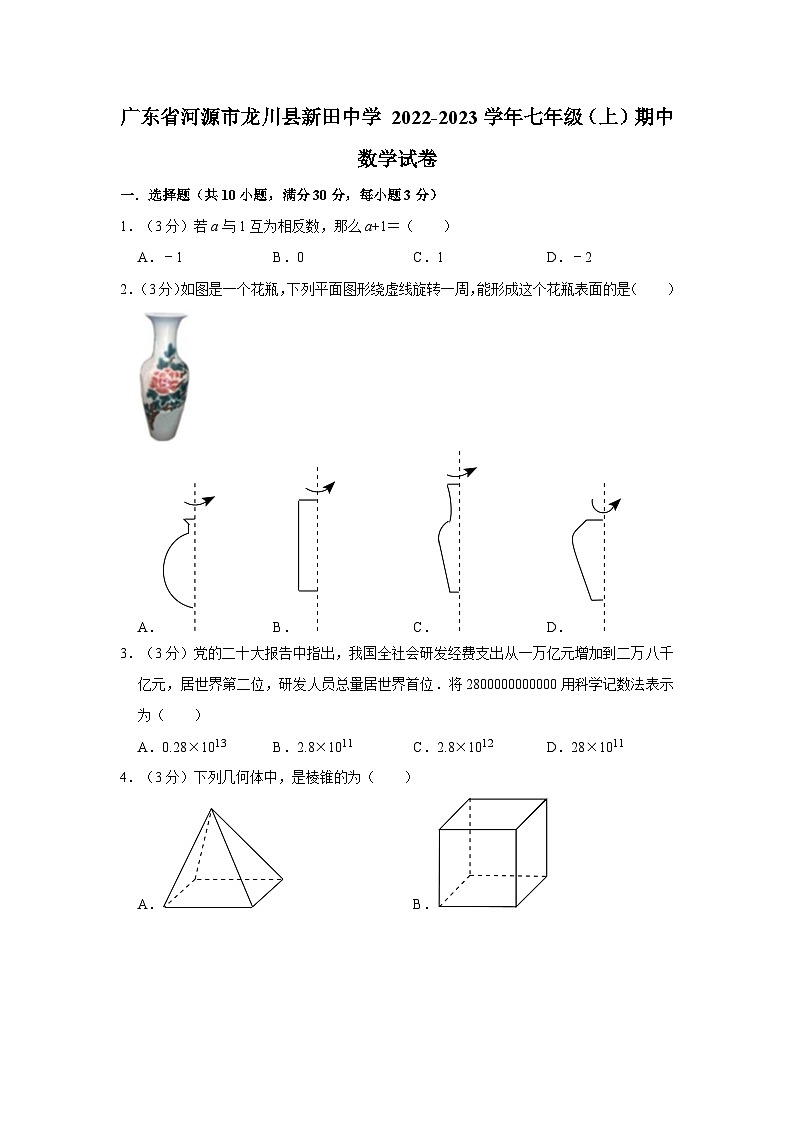
2．（3分）如图是一个花瓶，下列平面图形绕虚线旋转一周，能形成这个花瓶表面的是（　　）

A． B． C． D．

3．（3分）党的二十大报告中指出，我国全社会研发经费支出从一万亿元增加到二万八千亿元，居世界第二位，研发人员总量居世界首位．将2800000000000用科学记数法表示为（　　）

A．0.28×1013 B．2.8×1011 C．2.8×1012 D．28×1011

4．（3分）下列几何体中，是棱锥的为（　　）

A． B． 

C． D．

5．（3分）如图是一块6个面上分别写有“祝你新年快乐”的正方体展开平面图．在该正方体中，与“祝”字所在的面相对的面上的字为（　　）

A．新 B．年 C．快 D．乐

6．（3分）下列说法正确的是（　　）

A．x+是多项式 B．﹣m3次数是3，系数是1 

C．的常数项是1 D．数字﹣1是单项式

7．（3分）已知代数式2xay3与﹣xb+1ya+b是同类项，则a，b的值分别是（　　）

A． B． C． D．

8．（3分）若a+2b＝3，则多项式2a+4b﹣1的值为（　　）

A．3 B．4 C．5 D．6

9．（3分）已知|ab﹣4|+（b﹣2）2＝0，则a+b的值是（　　）

A．4 B．0 C．0或4 D．±2

10．（3分）脸面图案按一定的规律依次旋转形成下面排列，则第2012个图案是（　　）

A． B． C． D．

二．填空题（共5小题，满分15分，每小题3分）

11．（3分）数 3，﹣0.2，1，0，，中，负数有　   　个，正数有　   　个．

12．（3分）绝对值不大于10的所有整数的和是 　   　．

13．（3分）把一个学生使用的三角板以一条直角边为轴旋转成的形状是　     　体形状，其侧面展开图是　     　．

14．（3分）用代数式表示m与n的和除以10的商：　                  　．

15．（3分）若“!”是一种数学运算符号，并且：1!＝1，2!＝2×1＝2，3!＝3×2×1＝6，4!＝4×3×2×1，…，则＝　       　．

三．解答题（共8小题，满分75分）

16．（8分）计算：

（1）24+（﹣14）+（﹣16）+8；

（2）（﹣81）÷×÷（﹣8）．

17．（8分）由几个相同的边长为1的小立方块搭成的几何体的俯视图如图，格中的数字表示该位置的小立方块的个数．

（1）请在下面方格纸中分别画出这个几何体的主视图和左视图．

（2）根据三视图；这个组合几何体的表面积为 　     　个平方单位．（包括底面积）

（3）若上述小立方块搭成的几何体的俯视图不变，各位置的小立方块个数可以改变（总数目不变），则搭成这样的组合几何体中的表面积最大是为 　     　个平方单位．（包括底面积）

18．（8分）化简求值：

（1）4x2﹣（2x2+x﹣1）+（2﹣x2﹣3x），其中x＝﹣；

（2）5（3x2y﹣xy2）﹣（xy2+3x2y），其中x＝，y＝﹣1．

19．（9分）下列哪些说法正确？为什么？

（1）一个有理数如果不是整数，就是分数；

（2）一个有理数如果不是正数，就是负数．

20．（9分）若（x﹣2）2+|y+1|＝0，求4xy﹣（2x2+5xy﹣y2）+2（x2+2xy）的值．

21．（9分）如图，点A、B在数轴上表示的数分别为﹣12和8，两只蚂蚁M、N分别从A、B两点同时匀速出发，同向而行

（1）请填写表格；

（2）若两只蚂蚁在数轴上点P相遇，求点P在数轴上表示的数；

（3）若运动t秒钟时，两只蚂蚁的距离为10，求出t的值．

22．（12分）“十一”黄金周期间，贵州省锦屏县隆里古城在7天假期中每天接待的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数），把9月30日的游客人数记为a万人．

（1）请用含a的代数式表示10月2日的游客人数；

（2）请判断七天内游客人数最多的是哪天，有多少人？

（3）若9月30日的游客人数为2万人，门票每人10元，问黄金周期间隆里古城门票收入是多少元？

23．（12分）我们知道：4x+2x﹣x＝（4+2﹣1）x＝5x，类似地，若我们把（a+b）看成一个整体，则有4（a+b）+2（a+b）﹣（a+b）＝（4+2﹣1）（a+b）＝5（a+b）．这种解决问题的方法渗透了数学中的“整体思想”．“整体思想”是中学数学解题中的一种重要的思想方法，其应用极为广泛．请运用“整体思想”解答下面的问题：

（1）把（a﹣b）看成一个整体，合并3（a﹣b）2﹣7（a﹣b）2+2（a﹣b）2；

（2）已知：x2+2y＝5，求代数式﹣3x2﹣6y+21的值；

（3）已知a﹣2b＝3，2b﹣c＝﹣5，c﹣d＝10，求（a﹣c）+（2b﹣d）﹣（2b﹣c）的值．

参考答案与试题解析

一．选择题（共10小题，满分30分，每小题3分）

1． 解：∵a与1互为相反数，

∴a＝﹣1，

∴a+1＝﹣1+1＝0．

故选：B．

2． 解：将选项所给的平面图形绕虚线旋转一周，可得C选项符合所给图形，

故选：C．

3． 解：2800000000000＝2.8×1012．

故选：C．

4． 解：选项中的几何体分别为：A．棱锥；B．正方体；C．圆锥；D．圆柱．

故选：A．

5． 解：该正方体中，与“祝”字所在的面相对的面上的字为：年，

故选：B．

6． 解：A、分母中含有字母，不是整式，故A错误；

B、﹣m3次数是3，系数是﹣1，故B错误；

C、的常数项是，故C错误；

D、数字﹣1是单项式，故D正确．

故选：D．

7． 解：∵代数式2xay3与﹣xb+1ya+b是同类项，

∴，

解得：；

故选：B．

8． 解：∵a+2b＝3，

∴2a+4b﹣1

＝2（a+2b）﹣1

＝2×3﹣1

＝6﹣1

＝5．

故选：C．

9． 解：由题意得，ab﹣4＝0，b﹣2＝0，

解得b＝2，a＝±2，

则a+b＝0或4．

故选：C．

10． 解：∵观察图形发现图案每四个开始循环，

而2012÷4＝503，

∴第2012个图案是．

故选：A．

二．填空题（共5小题，满分15分，每小题3分）

11． 解：负数有：﹣0.2，﹣共2个；

正数有：3，1，共3个．

故答案为：2，3．

12． 解：绝对值不大于10的整数有：﹣10，﹣9，﹣8，﹣7，﹣6，﹣5，﹣4，﹣3，﹣2，﹣1，0，1，2，3，4，5，6，7，8，9，10，

它们之和是0．

故答案为：0．

13． 解：把一个学生使用的三角板以一条直角边为轴旋转成的形状是圆锥体形状，其侧面展开图是扇形．

故答案为：圆锥；扇形．

14． 解：m与n的和除以10的商为．

故答案为：．

15． 解：＝＝51×50＝2550．

故答案为：2550．

三．解答题（共8小题，满分75分）

16． 解：（1）24+（﹣14）+（﹣16）+8

＝24﹣14﹣16+8

＝32﹣30

＝2；

（2）（﹣81）÷×÷（﹣8）

＝81×××

＝2．

17． 解：（1）主视图有2列，每列小正方形数目分别为2，3；左视图有2列，每列小正方形数目分别为3，1，

图形分别如下：

（2）由题意可得：上面共有3个小正方形，下面共有3个小正方形；左面共有4个小正方形，右面共有4个正方形；前面共有5个小正方形，后面共有5个正方形，

故可得表面积为：1×（3+3+4+4+5+5）＝24．

（3）要使表面积最大，则需满足两正方体重合的最少，此时俯视图为：

这样上面共有3个小正方形，下面共有3个小正方形；左面共有5个小正方形，右面共有5个正方形；前面共有5个小正方形，后面共有5个正方形，

表面积为：1×（3+3+5+5+5+5）＝26．

故答案为：24、26．

18． （1）解：原式＝4x2﹣2x2﹣x+1+2﹣x2﹣3x＝x2﹣4x+3，

当x＝﹣时，原式＝（﹣）2﹣4×（﹣）+3，

＝﹣（﹣2）+3，

＝5；

（2）原式＝15x2y﹣5xy2﹣xy2﹣3x2y＝12x2y﹣6xy2，

当x＝，y＝﹣1时，

原式＝12×（）2×（﹣1）﹣6××（﹣1）2＝﹣3﹣3＝﹣6．

19． 解：（1）有理数分为：整数与分数，

∴有理数不是整数就是分数，

故说法正确；

（2）有理数分为：正有理数、负有理数、零，

∴有理数除了正有理数、负有理数，还有零，

故说法不正确．

20． 解：原式＝4xy﹣2x2﹣5xy+y2+2x2+4xy＝3xy+y2，

∵（x﹣2）2+|y+1|＝0，

∴x＝2，y＝﹣1，

则原式＝﹣6+1＝﹣5．

21． 解：（1）根据两只蚂蚁行驶的时间和路程，可以求出速度，再根据行驶时间计算出路程，进而填写表格，

（2）设相遇时间为x秒，由题意得，3x﹣2x＝8﹣（﹣12），

解得：x＝20，

20×3﹣12＝48

答：点P在数轴上表示的数为48．

（3）设运动时间为t秒，

①在相遇之前距离为10时，有3t+10﹣2t＝8﹣（﹣12），解得t＝10秒，

②在相遇之后距离为10时，有3t﹣10﹣2t＝8﹣（﹣12），解得t＝30秒，

答：当两只蚂蚁的距离为10，两只蚂蚁行驶的时间为10秒和30秒．

22． 解：（1）a+2.4（万人）；

（2）七天内游客人数分别是a+1.6，a+2.4，a+2.8，a+2.4，a+1.6，a+1.8，a+0.6，

所以3日人最多．

（3）（a+1.6）+（a+2.4）+（a+2.8）+（a+2.4）+（a+1.6）+（a+1.8）+（a+0.6）＝7a+13.2＝7×2+13.2＝27.2（万人），

∴黄金周期间该公园门票收入是27.2×10000×10＝2.72×106（元）．

23． 解：（1）3（a﹣b）2﹣7（a﹣b）2+2（a﹣b）2＝﹣2（a﹣b）2；

（2）﹣3x2﹣6y+21＝﹣3（x2+2y）+21，

当x2+2y＝5时，原式＝﹣3×5+21＝6；

（3）∵a﹣2b＝3，2b﹣c＝﹣5，c﹣d＝10，

∴a﹣c＝3+（﹣5）＝﹣2，2b﹣d＝﹣5+10＝5，

∴（a﹣c）+（2b﹣d）﹣（2b﹣c）

＝﹣2+5﹣（﹣5）

＝8．