2023年浙教版数学八年级（上）期中试卷（附答案）

八年级（上）期中仿真模拟试卷

一、选择题（每题3分，共30分）

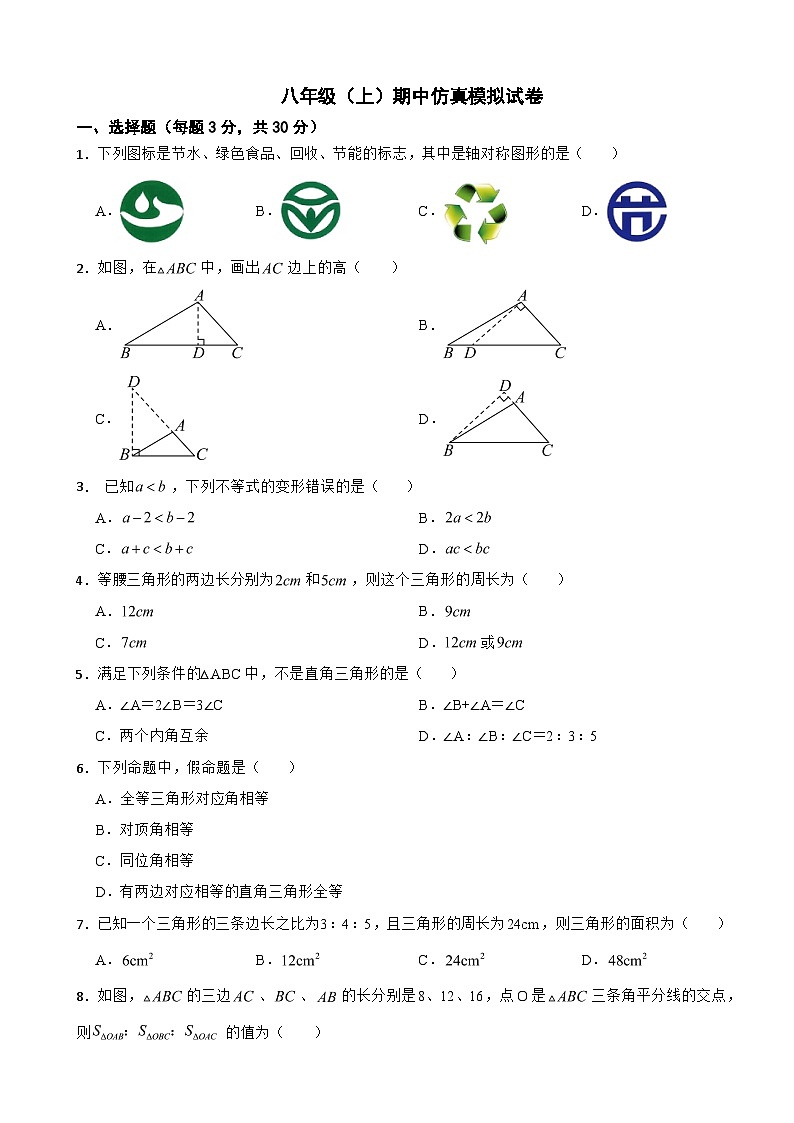
1．下列图标是节水、绿色食品、回收、节能的标志，其中是轴对称图形的是（　　）

A． B． C． D．

2．如图，在中，画出边上的高（　　）

A． B．

C． D．

3． 已知，下列不等式的变形错误的是（　　）

A． B．

C． D．

4．等腰三角形的两边长分别为和，则这个三角形的周长为（　　）

A． B．

C． D．或

5．满足下列条件的△ABC中，不是直角三角形的是（　　）

A．∠A＝2∠B＝3∠C B．∠B+∠A＝∠C

C．两个内角互余 D．∠A：∠B：∠C＝2：3：5

6．下列命题中，假命题是（　　）

A．全等三角形对应角相等

B．对顶角相等

C．同位角相等

D．有两边对应相等的直角三角形全等

7．已知一个三角形的三条边长之比为3：4：5，且三角形的周长为24cm，则三角形的面积为（　　）

A． B． C． D．

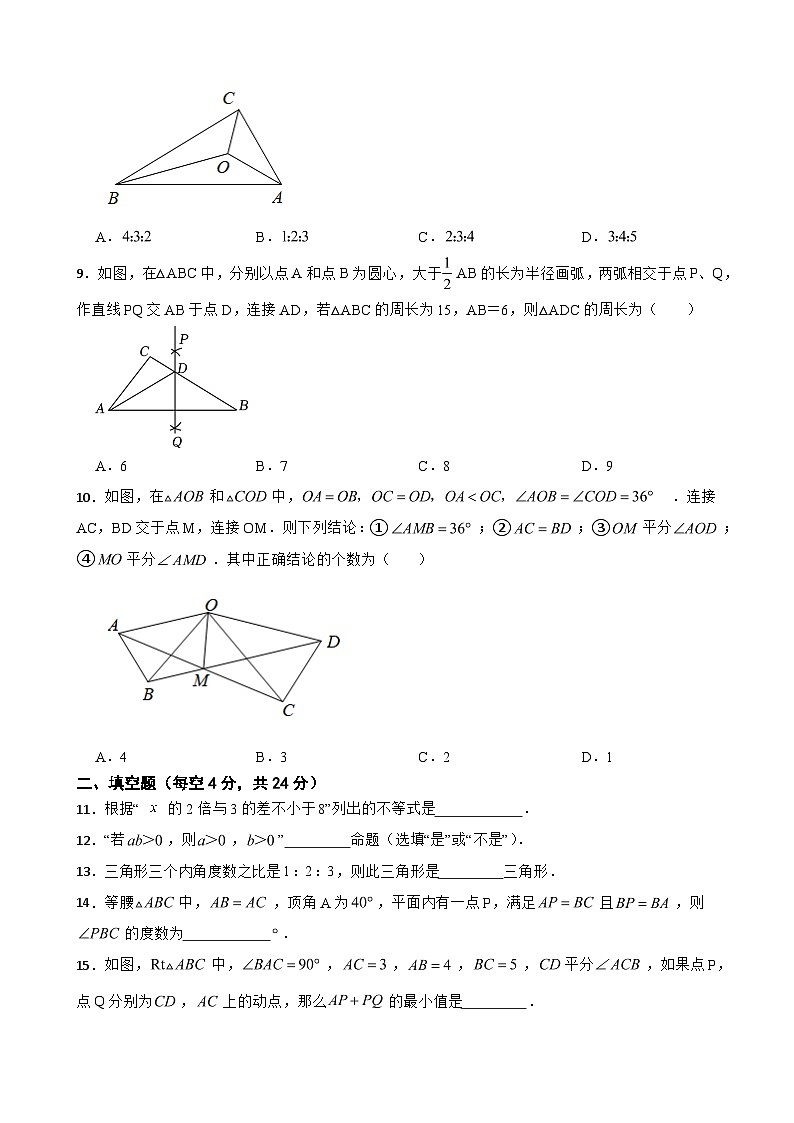
8．如图，的三边、、的长分别是8、12、16，点O是三条角平分线的交点，则的值为（　　）

A． B． C． D．

9．如图，在△ABC中，分别以点A和点B为圆心，大于AB的长为半径画弧，两弧相交于点P、Q，作直线PQ交AB于点D，连接AD，若△ABC的周长为15，AB＝6，则△ADC的周长为（　　） 

A．6 B．7 C．8 D．9

10．如图，在和中，．连接AC，BD交于点M，连接OM．则下列结论：①；②；③平分；④平分．其中正确结论的个数为（　　）

A．4 B．3 C．2 D．1

二、填空题（每空4分，共24分）

11．根据“ 的2倍与3的差不小于8”列出的不等式是　        　．

12．“若，则，”　     　命题（选填“是”或“不是”）．

13．三角形三个内角度数之比是1：2：3，则此三角形是　     　三角形．

14．等腰中，，顶角A为，平面内有一点P，满足且，则的度数为　        　．

15．如图，中，，，，，平分，如果点P，点Q分别为，上的动点，那么的最小值是　     　．

16．图1是小馨在“天猫双12”活动中购买的一张多档位可调节靠椅．档位调节示意图如图2所示，已知两支脚米，米，为上固定连接点，靠背米．档位为Ⅰ档时，，档位为Ⅱ档时，当靠椅由Ⅰ档调节为Ⅱ档时，靠背顶端向后靠的水平距离即为　     　米．

三、解答题（共8题，共66分）

17．解不等式，并将解集在数轴上表示出来.

（1）；

（2）.

18．图①、图②、图③均是6×4的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点叫做格点，的顶点均在格点上，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上． 

（1）在图①中以为边，画一个等腰； 

（2）在图②中画，使与关于直线对称； 

（3）在图③中画，使与全等． 

19．如图，中，是的中线，是的角平分线，是的高．

（1）若的面积为8，，求的长；

（2）若，求的度数．

20．如图，在平面直角坐标系中，点，连接，将绕点逆时针方向旋转到．

（1）求点的坐标；用字母，表示

（2）如图，延长交轴于点，过点作交轴于点，求证：．

21．如图，某人从A地到B地共有三条路可选，第一条路是从A到B，AB为10米，第二条路是从A经过C到达B地，AC为8米，BC为6米，第三条路是从A经过D地到B地共行走26米，若C、B、D刚好在一条直线上.

（1）求证：；

（2）求AD和BD的长.

22．如图，在中，的垂直平分线交于点，交于点，于，．

（1）求证：为线段的中点．

（2）若，求的度数．

23．如图，点是等边内一点，点是外的一点，，连接．

（1）求证：是等边三角形；

（2）若，，，求的长．

24．【问题背景】

（1）如图1，点P是线段，的中点，求证：；

（2）【变式迁移】
如图2，在等腰中，是底边上的高线，点E为内一点，连接，延长到点F，使，连接，若，若，，求的长；

（3）【拓展创新】
如图3，在等腰中，，，点D为中点，点E在线段上（点E不与点B，点D重合），连接，过点A作，连接，若，，请直接写出的长.

1．B

2．D

3．D

4．A

5．A

6．C

7．C

8．A

9．D

10．B

11．2x-3≥8

12．是

13．直角

14．30或110

15．

16．0.14

17．（1）解：，

移项得，

合并得，

用数轴表示为：

（2）解，

去分母得，

去括号得，

移项得，

合并得，

系数化为得，

用数轴表示为：

18．（1）解：如图① ，即为所求； 

（2）解：如图② ，即为所求； 

（3）解：如图③ ，即为所求． 

19．（1）解：由题意可得：，

即，

∴，

又为的中线，

∴，

（2）解：∵是的高，，

∴

又是的角平分线

∴

∴

20．（1）解：如图，

作轴于，作轴于，

，

，

，

，

，

在和中，

，

≌，

，，

；

（2）证明：如图，

设，交于点，

，

，

，

，

，

，

即：，

，

≌，

．

21．（1）证明：根据题目条件有：米，米，米，

即：，

∴是直角三角形，且为斜边，

∴

（2）解：根据题意有：，

∴，

∵米，

∴，

∵米，，

∴在中，有：，

∴，

解得：米，

∴米，

即：米，米

22．（1）证明：连接AE ，如图所示，

∵EF垂直平分AB ，

，

，

，

△ACE是等腰三角形，

，

∴D是EC的中点，

（2）解：设 ；

，

，

，

，

，

在三角形ABC中， ，

解得 ，

．

23．（1）证明：∵，

∴，

∵为等边三角形，

∴，

∴，

即，

∴是等边三角形．

（2）解：∵，，

∴，

∵，

∴，

∵是等边三角形．

∴，，

∴，

，

∴在中，，

∴．

24．（1）证明：点P是线段，的中点，

，，

在和中，

，

，

；

（2）解：如图：连接，

在等腰中，是底边上的高线，

，

在和中，

，

，，

，

，

，

，，

，

；

（3）解：