江苏省扬州市仪征市实验教育集团2023-2024学年九年级上学期10月质量抽测数学试卷（月考）

九年级数学试卷        2023.10.16

一、选择题（8×3=24分）

1. 将方程（x﹣1）2＝6化成一元二次方程的一般形式，正确的是(　▲　)  

A. x2﹣2x+5＝0    B. x2﹣2x﹣5＝0    C. x2+2x﹣5＝0   D. x2+2x+5＝0

2.某鞋店对某款女鞋一周的销售情况进行统计，结果如下：

根据上表信息，该店主决定下周多进一些37码的鞋子，影响店主进货决策的统计量是(　▲　)

A．中位数            B．众数            C．平均数      D．方差

3. 已知圆锥的底面半径为3cm，母线长为5cm，则此圆锥的侧面积为 (　▲　)

A. 15πcm2 B. 20πcm2 C. 25πcm2 D. 30πcm2

4. 如图，在△ABC中，∠ACB=90°，AB=5，BC=4．以点A为圆心，r为半径作圆，当点C在⊙A内且点B在⊙A外时，r的值可能是(　▲　)  

 A. 2                B. 3                C. 4              D. 5

5. 如图，AB是⊙O的直径，DA切⊙O于点A，DO交⊙O于点C，连接BC，若∠D=40°，则∠ABC为(　▲　)  

A. 20° B. 25° C. 40            D. 50°

     第4题                      第5题                   第6题                   第7题

6. 如图,在正八边形ABCDEFGH中,AE与BG交于点P,则∠APG的度数为(　▲　)

A.108°            B.112.5°        C.120°         D.135°

7. 如图，在平面直角坐标系中，点在第一象限，⊙P与x轴、y轴都相切，且经过矩形AOBC的顶点C，与BC相交于点D，若⊙P的半径为5，点的坐标是（0,8），则点D的坐标是(　▲　)

A.（9,2） B.（9,3） C.（10,2）        D.（10,3）

8. 若a是方程x－x－1=0的一个根，则－a+2a+2023的值为(　▲　) 

A. 2022            B. －2022        C. 2023          D. －2023

二、填空题（10×3=30分）

9.七个同学定点投篮（每人投10个），投进的个数分别为6，10，5，3，4，8，4，这组数据的极差是    ▲    ．

10.如图，在⊙O中，∠BOC=54°，则∠BAC的度数为    ▲    ．

第10题                第15题                 第17题                    第18题

11.一元二次方程的一根为2，则另一根为    ▲    ．

12.已知△ABC三边长分别为5cm，12cm，13cm，则这个三角形的外接圆的半径为    ▲    cm．

13.小明参加“强国有我”主题演讲比赛，其演讲形象、内容、效果三项的成绩分别是70分、90分、80分．若将三项得分依次按2：4：4的比例确定最终成绩，则小明的最终比赛成绩为

    ▲     分．

14.若关于x的一元二次方程kx2﹣2x﹣1＝0有两个不相等的实数根，则k的取值范围是    ▲    ．

15.如图，数学活动课上，小明用边长为10cm的正五边形纸片材料制作圆锥，他以D为圆心，DC为半径作扇形DEC，将该扇形围成圆锥的侧面，则这个圆锥底面圆的半径是    ▲    cm．

16.某次商品交易会上，所有参加会议的任意两个商家之间都签订了一份合同，共签订合同45份，那么共有    ▲    个商家参加了交易会．

17.如图，在边长为2的正方形ABCD中，以点D为圆心．AD的长为半径画弧，再以BC为直径画半圆．若阴影部分①的面积为S1，阴影部分②的面积为S2，则S2-S1的值为    ▲    ．

18.如图，在正方形ABCD中，边长为6， E为BC边上一点，CE=2BE，连接DE．在正方形ABCD外部找一点P，使得∠DEC+∠DPC=180°，则线段BP的最大值为    ▲    ．

三、解答题（96分）

19.（8分）解方程：

（1）      （2）

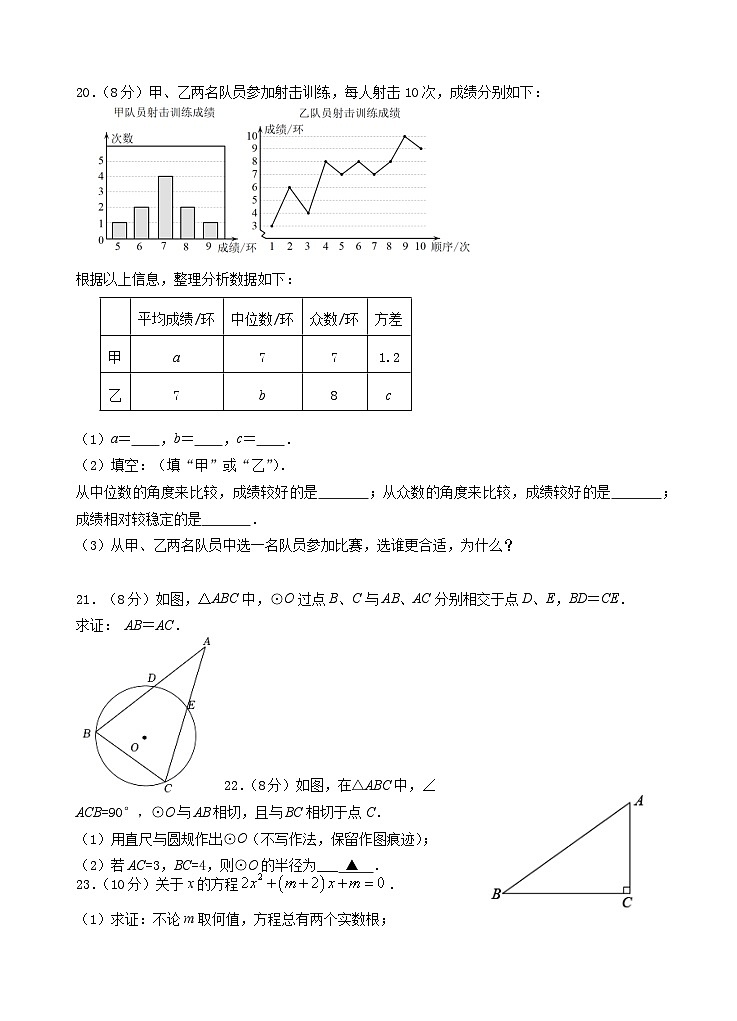
20．（8分）甲、乙两名队员参加射击训练，每人射击10次，成绩分别如下：

根据以上信息，整理分析数据如下：

（1）a＝　　，b＝　　，c＝　　．

（2）填空：（填“甲”或“乙”）．

从中位数的角度来比较，成绩较好的是　　   ；从众数的角度来比较，成绩较好的是　　   ；成绩相对较稳定的是　　   ．

（3）从甲、乙两名队员中选一名队员参加比赛，选谁更合适，为什么？

21．（8分）如图，△ABC中，⊙O过点B、C与AB、AC分别相交于点D、E，BD＝CE．

求证： AB＝AC．

22．（8分）如图，在△ABC中，∠ACB=90°，⊙O与AB相切，且与BC相切于点C．

（1）用直尺与圆规作出⊙O（不写作法，保留作图痕迹）；

（2）若AC=3，BC=4，则⊙O的半径为___ ▲  ．

23．（10分）关于x的方程．

（1）求证：不论m取何值，方程总有两个实数根；

（2）若方程有两个相等的实数根，请求出m的值并求此时方程的根．

24．（10分）阅读下面的例题与解答过程：

例.解方程：x2-|x|-2=0

解：当x≥0时，原方程可化为x2-x-2=0，解得x1=2,x2=-1（不合题意，舍去）；

当x＜0时，原方程可化为x2+x-2=0，解得x1=1,x2=-2（不合题意，舍去）；

∴原方程的解是x1=2,x2=-2.

在上面的解答过程中，我们对x进行讨论，从而化简绝对值.这是解决数学问题的一种重要思想---分类讨论.请仿照上述例题的解答过程，解下列方程：

(1) x2-2|x|=0；       (2) x2-2x-4|x-1|-4=0

25．（10分）如图，在Rt△ABC中，∠ACB＝90°，⊙O与BC，AC分别相切于点E，F，BO平分∠ABC，连接OA．

（1）求证：AB是⊙O的切线；

（2）若BE＝AC＝3，⊙O的半径是1，求图中阴影部分的面积．

26．（10分）如图，在一块长32m，宽24m的矩形绿地内，建一个矩形花圃．

（1）要使矩形花圃的面积是矩形绿地面积的一半，且矩形花圃四周的绿地等宽，求四周绿地的宽；

（2）要使矩形花圃的面积是矩形绿地面积的一半，且矩形花圃的周长是矩形绿地周长的一半，问这样的矩形花圃能否围出？如果能，请求出矩形花圃的长和宽；如果不能，请说明理由．

27．（12分）如图，在矩形ABCD中，AB=4，BC=6．点E为CD边上的一个动点（不与C、D重合），⊙O是△BCE的外接圆．

（1）若CE=2，⊙O交AD于点F、G，求⊙O 的半径及FG的长度；

（2）若CE的长度为m，⊙O与直线AD的位置关系随着m的值变化而变化，试探索⊙O与直线AD的位置关系及对应的m的取值范围．

28. （12分）

【数学史料】

19世纪英国著名文学家和历史学家卡莱尔给出了一元二次方程的几何解法：如图1，在平面直角坐标系中，已知点A（0，1）、B（−b，c），以AB为直径作⊙P．若⊙P交x轴于点M（m，0）、N（n，0），则m、n为方程两个实数根．

【理解结论】

由勾股定理得，AM2＝12+m2，BM2＝c2+（−b−m）2，AB2＝（1−c）2+b2，在Rt△ABM中，AM2+BM2＝AB2，所以12+m2+c2+（−b−m）2＝（1−c）2+b2．化简得：m2+bm+c＝0．同理可得：n2+bn+c＝0．所以m、n为方程的两个实数根．

【运用结论】

（1）在图2中的x轴上画出以方程x2−3x−2＝0两根为横坐标的点M、N．

（2）已知点A（0，1）、B（6，9），以AB为直径作⊙C．判断⊙C与x轴的位置关系，并说明理由．

【拓展探索】

（3）在平面直角坐标系中，已知两点A（0，a）、B（−b，c），若以AB为直径的圆与交x轴有两个交点M、N，则以点M、N的横坐标为根的一元二次方程是什么？