2024年数学高考大一轮复习第三章 §3.2　导数与函数的单调性（附答单独案解析）

1．函数f(x)＝xln x＋1的单调递减区间是(　　)

A.   B.

C.   D．(e，＋∞)

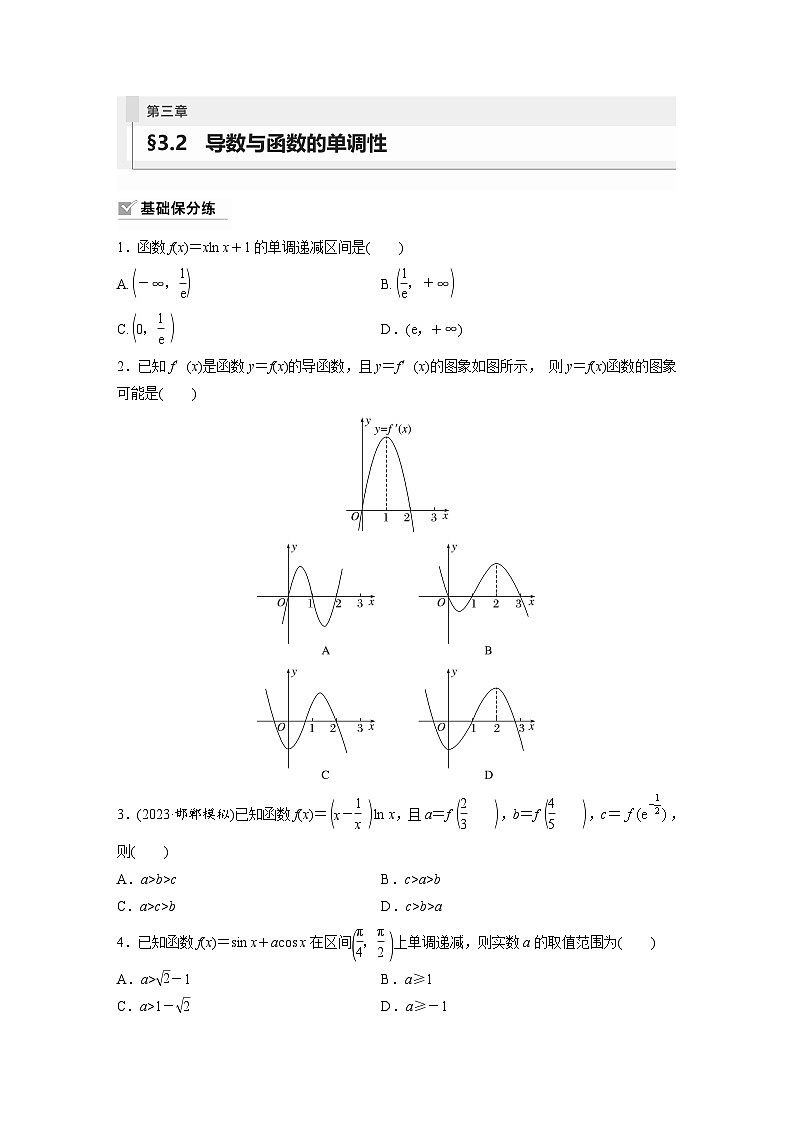
2．已知f′(x)是函数y＝f(x)的导函数，且y＝f′(x)的图象如图所示， 则y＝f(x)函数的图象可能是(　　)

3．(2023·邯郸模拟)已知函数f(x)＝ln x，且a＝f ，b＝f ，c＝，则(　　)

A．a>b>c   B．c>a>b

C．a>c>b   D．c>b>a

4．已知函数f(x)＝sin x＋acos x在区间上单调递减，则实数a的取值范围为(　　)

A．a>－1   B．a≥1

C．a>1－   D．a≥－1

5．若f(x)＝sin x＋x3＋x，则不等式f(x＋1)＋f(2x)>0的解集是(　　)

A.   B.

C.   D.

6．如果函数f(x)对定义域内的任意两实数x1，x2(x1≠x2)都有>0，则称函数y＝f(x)为“F函数”．下列函数是“F函数”的是(　　)

A．f(x)＝ex   B．f(x)＝x2

C．f(x)＝ln x   D．f(x)＝sin x

7．函数f(x)＝(2x－1)ex的单调递增区间为________________．

8．已知函数f(x)＝＋＋ax＋1存在三个单调区间，则实数a的取值范围是________．

9．已知函数f(x)＝x3＋ax2＋1，a∈R.

(1)讨论函数f(x)的单调区间；

(2)若函数f(x)的单调递减区间是，求a的值．

10．已知a∈R，函数f(x)＝(－x2＋ax)ex，x∈R.

(1)当a＝2时，求函数f(x)的单调递增区间；

(2)若函数f(x)在(－1,1)上单调递增，求实数a的取值范围．

11．设函数f(x)＝ln x＋，若对任意b>a>1，<1恒成立，则m的取值范围是(　　)

A．[0，＋∞)   B．(0，＋∞)

C.   D.

12．已知函数f(x)＝－2x2＋ln x(a>0)，若函数f(x)在[1,2]上不单调，则实数a的取值范围是________．

13．已知a>b>0，且，则(　　　)

A．0<b<   B．0<b<1

C．1<b<e   D．b>e

14．(2023·蚌埠模拟)若x1·＝x2·log2x2＝2 024，则x1x2的值为________．