备战2024新高考-高中数学二轮重难点专题13-w的取值范围与最值问题

这是一份备战2024新高考-高中数学二轮重难点专题13-w的取值范围与最值问题，文件包含2024新高考二轮重难点专题13ω的取值范围与最值问题原卷版docx、2024新高考二轮重难点专题13ω的取值范围与最值问题解析版docx等2份教案配套教学资源，其中教案共22页， 欢迎下载使用。
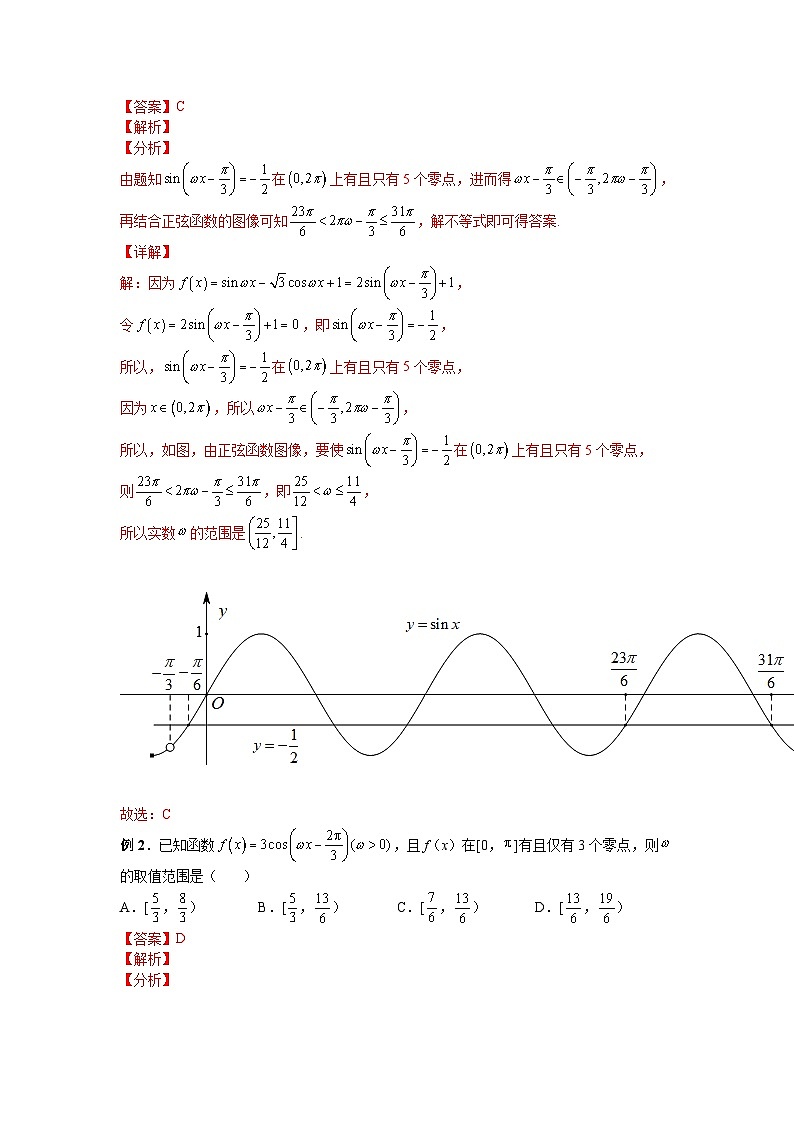
2024高考数学二轮复习重难点专题13ω 的取值范围与最值问题【考点预测】1.在区间内没有零点同理，在区间内没有零点2.在区间内有个零点同理在区间内有个零点          3. 在区间内有个零点 同理在区间内有个零点4. 已知一条对称轴和一个对称中心，由于对称轴和对称中心的水平距离为，则．5.已知单调区间，则.【方法技巧与总结】解决ω的取值范围与最值问题主要方法是换元法和卡住ω的大致范围.【题型归纳目录】题型一：零点问题题型二：单调问题题型三：最值问题题型四：极值问题题型五：对称性题型六：性质的综合问题【典例例题】题型一：零点问题例1．已知函数在上有且只有5个零点，则实数的范围是（       ）A． B． C． D．     例2．已知函数，且f（x）在[0，]有且仅有3个零点，则的取值范围是（       ）A．[，） B．[，） C．[，） D．[，）        例3．若关于的方程在上有实数根，则实数的取值范围是________．                   题型二：单调问题例4．将函数图象上所有点的横坐标缩短到原来的倍纵坐标不变，再向左平移个单位长度，得到函数的图象，若在上单调递减，则实数的取值范围为（       ）A． B． C． D．             例5．设，函数，，若在上单调递增，且函数与的图象有三个交点，则的取值范围（       ）A． B． C． D．              题型三：最值问题例6．已知函数的定义域为，值域为，则的取值范围是（       ）A． B．C． D．        例7．已知函数，若函数的图象在区间上的最高点和最低点共有个，下列说法正确的是___________.①在上有且仅有个零点；②在上有且仅有个极大值点；③的取值范围是；④在上为单递增函数.           题型四：极值问题例8．若函数（）在上单调，且在上存在极值点，则ω的取值范围是（       ）A． B． C． D．            例9．已知偶函数（，）在上恰有2个极大值点，则实数的取值范围为（       ）A． B．C． D．              题型五：对称性例10．已知函数在内有且仅有三条对称轴，则的取值范围是（       ）A． B． C． D．         题型六：性质的综合问题例11．设函数在区间恰有三个极值点、两个零点，则的取值范围是（       ）A． B． C． D．                    （多选题）例12．已知函数，则下列结论中正确的是（       ）A．若ω=2，则将的图象向左平移个单位长度后得到的图象关于原点对称B．若 ，且 的最小值为，则ω=2C．若在[0， ]上单调递增，则ω的取值范围为（0，3]D．若在[0，π]有且仅有3个零点，则ω的取值范围是                                  （多选题）例13．已知，则下列判断中，错误的是（       ）A．若，，且，则B．存在，使得的图像右移个单位长度后得到的图像关于轴对称C．若在上恰有7个零点，则的取值范围为D．若在上单调递增，则的取值范围为