初中数学第二十六章 反比例函数26.1 反比例函数26.1.2 反比例函数的图象和性质教学ppt课件

这是一份初中数学第二十六章 反比例函数26.1 反比例函数26.1.2 反比例函数的图象和性质教学ppt课件，共17页。PPT课件主要包含了教学目标，教学重难点，教学设计，y1y2，y2y1y3，cab，k＝ab，活动4例题与练习，活动5等内容，欢迎下载使用。

1．分析实际问题中变量之间的关系建立反比例函数模型，进而解决实际问题．2．体会数学与现实生活的紧密性，体会数形结合的数学思想．3．培养学生运用代数方法解决实际问题的能力．
灵活运用反比例函数性质解决问题．
反比例函数的图象和性质的综合应用．
活动1 新课导入
1．若点A(7，y1)，B(5，y2)在双曲线 y＝－ 上，则y1，y2的大小关系为__________．2．若点(－2，y1)，(－1，y2)，(1，y3)在反比例函数 y＝ (k<0)的图象上，则y1，y2，y3的大小关系为____________．3．点A(－2，a)，B(－1，b)，C(3，c)在双曲线 y＝ (k>0)上，试确定a，b，c的大小关系为________．
活动2 探究新知
1．教材P7例3.提出问题：(1)点A(2，6)在第几象限？因为反比例函数的图象经过点A(2，6)，所以这个函数图象的两支分别位于第几象限？在每一个象限内，y随x的增大而怎样变化？(2)对于第(1)问，还有其他的解答方法吗？要判断函数的性质，我们首先可以求反比例函数的解析式？求反比例函数的解析式一般用什么方法？请同学们试着用待定系数法求出这个函数的解析式，并根据该函数的图象和性质解答第(1)问；(3)我们如何判断点在不在函数的图象上？
2．教材P7例4.提出问题：(1)反比例函数图象的分布有哪几种可能？由图可知这个函数的图象的一支位于第几象限？所以另一支必位于第几象限？怎么求常数m的取值范围？(2)要比较y1和y2的大小，可以根据反比例函数的什么来解答？因为m－5>0，所以这个函数的性质是什么？因此当x1>x2时，y1和y2有怎样的大小关系？(3)第(2)问除了课本上的解答方法，还有其他方法吗？请试着用图象法或数形结合法比较y1和y2的大小．
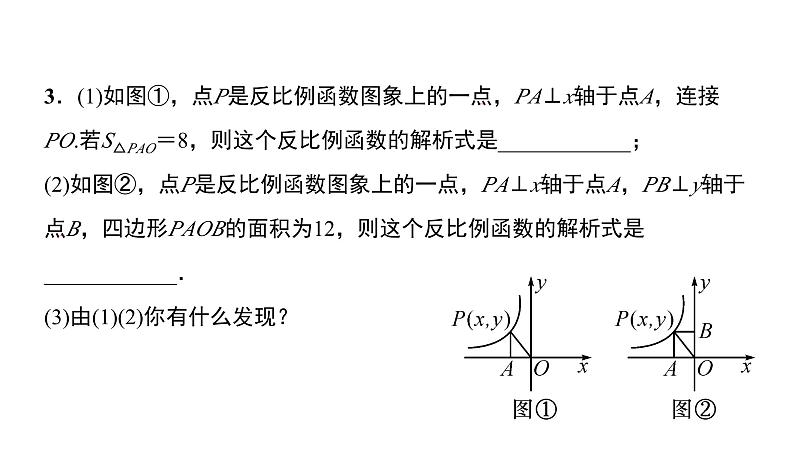
3．(1)如图①，点P是反比例函数图象上的一点，PA⊥x轴于点A，连接PO.若S△PAO＝8，则这个反比例函数的解析式是____________；(2)如图②，点P是反比例函数图象上的一点，PA⊥x轴于点A，PB⊥y轴于点B，四边形PAOB的面积为12，则这个反比例函数的解析式是____________．(3)由(1)(2)你有什么发现？
已知反比例函数的图象经过点A(a，b)(其中a≠0，b≠0)，可求出这个反比例函数的解析式．解题步骤如下：(1)设这个反比例函数的解析式为____________；(2)把 x＝____，y＝____代入这个反比例函数的解析式，解出________；(3)所求的反比例函数为__________；(4)过点A作x轴，y轴的垂线，两垂线与两坐标轴围成的矩形面积S＝ ______ ．
活动3 知识归纳
例1　如图，一次函数y＝kx＋b的图象与反比例函数 的图象相交于A，B两点．
(1)根据图象，写出点A，B的坐标；(2)求出两函数的解析式；(3)根据图象回答：当x为何值时，一次函数的函数值大于反比例函数的函数值．
解：(1)A(－6，－2)，B(4，3)；
把 A(－6，－2)，B(4，3)代入 y＝kx＋b，得
(3)由图象可知，当－64时，一次函数的函数值大于反比例函数的函数值．
例2　如图，已知反比例函数 y＝ (k>0)的图象经过点A(1，m)，过点A作AB⊥y轴于点B，且△AOB的面积为1.(1)求m，k的值；(2)若一次函数 y＝nx＋2(n≠0)的图象与反比例函数 y＝ 的图象有两个不同的公共点，求实数n的取值范围．
解：(1)由已知，得S△AOB＝ ×1×m＝1，解得m＝2，把A(1，2)代入y＝ ，得k＝2；
(2)由(1)知反比例函数解析式是 y＝ ，则 ＝nx＋2有两个不同的解，方程去分母，得nx2＋2x－2＝0，则Δ＝ 4＋8n>0，解得n>－ 且n≠0.
1．教材P8练习第1，2题．
2．反比例函数 y＝ 与正比例函数y＝2kx在同一个坐标系中的图象不可能是下列选项中的(　 　)
3．如图，双曲线 y＝ 与直线 y＝－ x 交于A，B两点，且点A(－2，m)，则点B的坐标是(　 　)
A．(2，－1)　　　 　 　B．(1，－2)
4．如图，已知反比例函数 y＝ 的图象的一支位于第一象限．(1)判断该函数图象的另一支所在的象限，并求m的取值范围；(2)O为坐标原点，点A在该反比例函数位于第一象限的图象上，点B与点A关于x轴对称，若△OAB的面积为6，求m的值．
解：(1)根据反比例函数的图象关于原点对称知，该函数图象的另一支在第三象限，且m－7>0，则m>7；
(2)设线段AB交x轴于点C.∵点B与点A关于x轴对称，若△OAB的面积为6, 则△OAC的面积为3，∴ (m－7)＝3，∴m＝13.
完成《名师测控》随堂反馈手册《精英新课堂》变式训练手册
活动6 课堂小结
1．反比例函数图象上点的坐标特征．2．反比例函数与一次函数的交点问题．3．反比例函数中系数k的几何意义．