2022-2023学年辽宁省营口市大石桥市八年级（下）期末数学试卷（含答案解析）

2022-2023学年辽宁省营口市大石桥市八年级（下）期末数学试卷

1.下列各根式中，最简二次根式是(    )

A.  B.  C.  D.

2.下列各组数中，能构成直角三角形的是(    )

A. 4，5，6 B. 1，1， C. 6，8，11 D. 5，12，10

3.下列各式计算错误的是(    )

A.  B.
C.  D.

4.如图，平行四边形ABCD的对角线AC与BD相交于点O，，若，，则BD的长是(    )

A. 38 B. 28 C. 34 D. 35

5.下列说法中不正确的是(    )

A. 对角线垂直的平行四边形是菱形 B. 对角线相等的平行四边形是矩形
C. 菱形的面积等于对角线乘积的一半 D. 对角线互相垂直平分的四边形是正方形

6.某同学对数据26，36，36，46，，52进行统计分析发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是(    )

A. 平均数 B. 中位数 C. 方差 D. 众数

7.如图，在平面直角坐标系中，的顶点A、C的坐标分别为、，，，过B作x轴垂线交x轴于点M，作y轴垂线交y轴于点N，则矩形OMBN的面积为(    )

A.
B. 9
C.
D.

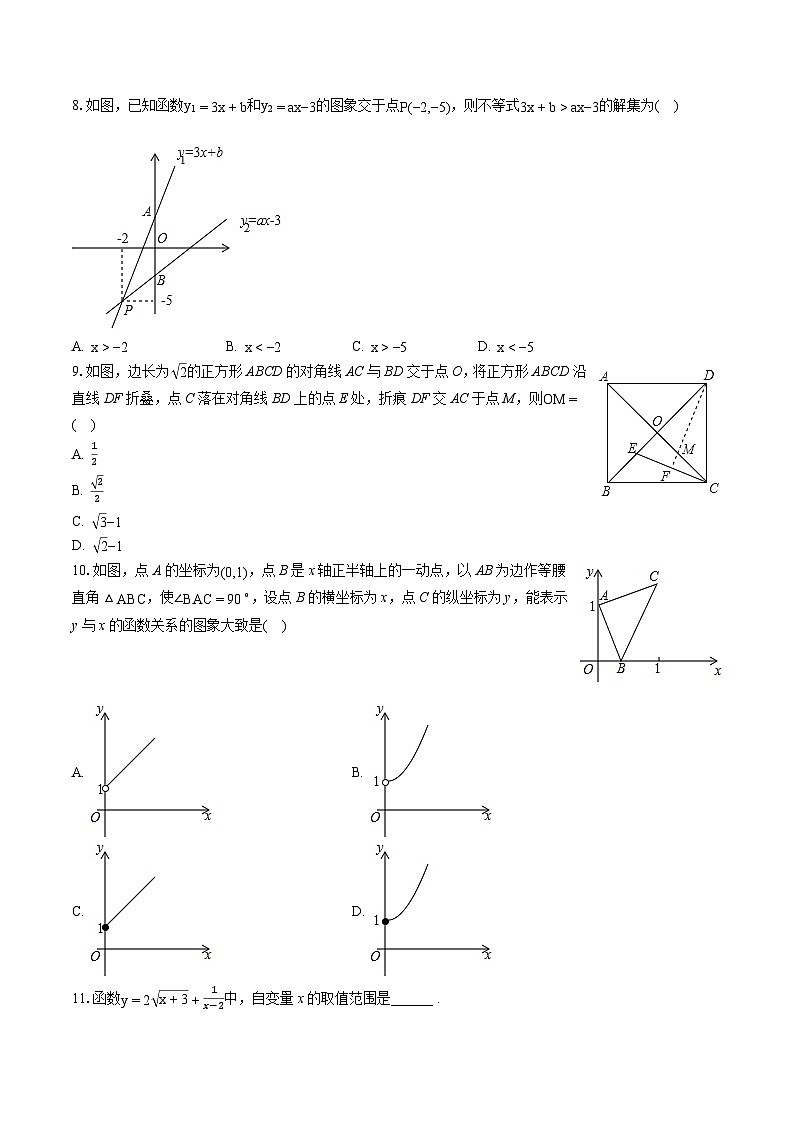
8.如图，已知函数和的图象交于点，则不等式的解集为(    )

 

A.  B.  C.  D.

9.如图，边长为的正方形ABCD的对角线AC与BD交于点O，将正方形ABCD沿直线DF折叠，点C落在对角线BD上的点E处，折痕DF交AC于点M，则(    )

A.
B.
C.
D.

10.如图，点A的坐标为，点B是x轴正半轴上的一动点，以AB为边作等腰直角，使，设点B的横坐标为x，点C的纵坐标为y，能表示y与x的函数关系的图象大致是(    )

A.  B.
C.  D.

11.函数中，自变量x的取值范围是______ .

12.若函数是一次函数，则______ .

13.若数据1，4，a，9，6，5的平均数为5，则中位数是______；众数是______.

14.若直角三角形的两边长为6和8，则第三边长为______.

15.如图，一次函数的图象与x轴、y轴分别交于点A、B，点M在x轴上，要使是以AB为腰的等腰三角形，那么点M的坐标是______.

 

16.如图，将矩形ABCD折叠，使点C和点A重合，折痕为EF，EF与AC交于点若，，则AO的长为______.

17.计算：

18.计算：

19.在杭州西湖风景游船处，如图，在离水面高度为5m的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为13m，此人以的速度收绳后船移动到点D的位置，问船向岸边移动了多少m？假设绳子是直的，结果保留根号

20.如图，在▱ABCD中，点E是CD边的中点，连接AE并延长交BC的延长线于点F，连接BE，
求证：AE平分；
若，，求▱ABCD的面积.

21.甲、乙两车分别从A、B两地同时出发，沿同一条公路相向行驶，相遇后，甲车继续以原速行驶到B地，乙车立即以原速原路返回到B地.甲、乙两车距B地的路程与各自行驶的时间之间的关系如图所示.
______ ，______ .
分别求出甲、乙两车距B地的距离y与行驶的时间x之间的函数关系式.
当甲车到达B地时，求乙车距B地的路程.

22.本学期初，某校为迎接中华人民共和国建国七十周年，开展了以“不忘初心，缅怀革命先烈，奋斗新时代”为主题的读书活动．校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”下面简称：“读书量”进行了随机抽样调查，并对所有随机抽取学生的“读书量”单位：本进行了统计，如图所示：

根据以上信息，解答下列问题：
补全上面两幅统计图，填出本次所抽取学生四月份“读书量”的众数为______.
求本次所抽取学生四月份“读书量”的平均数；
已知该校七年级有1200名学生，请你估计该校七年级学生中，四月份“读书量”为5本的学生人数．

23.如图，在▱ABCD中，对角线AC，BD相交于点O，以AC为斜边的等腰直角三角形AEC的边CE，与AD交于点F，连接OE，使得在AD上截取，连接EH，
判断四边形ABCD的形状，并说明理由；
若，，求EH的长．

24.某市风景区门票价格如图所示，现有甲乙两个旅行团队，计划在“十一”黄金周期间到该景点游玩．两团队游客人数之和为120人，甲团队人数不超过50人，乙团队人数为x人，但不足100人．如果甲、乙两团队分别购买门票，两团队门票款之和为W元．
求W关于x的关系式，并说明两队联合购票比分别购票最多可节约多少元？
“十一”黄金周之后，该风景区对门票价格作了如下调整：人数不超过50人时，门票价格不变；人数超过50人但不超过100人时，每张门票降价a元；人数超过100人时，每张门票降价2a元，若甲、乙两个旅行团队“十一”黄金周之后去游玩，最多节约3400元，求a的值．

答案和解析

1.【答案】A 

【解析】解：A、是最简二次根式，此选项符合题意；
B、，不是最简二次根式，此选项不符合题意，排除；
C、，不是最简二次根式，此选项不符合题意，排除；
D、，不是最简二次根式，此选项不符合题意，排除；
故选：
直接利用最简二次根式的定义逐项判断即可．
此题主要考查了最简二次根式的定义，解题的关键是判断最简二次根式的过程中要注意：在二次根式的被开方数中，只要含有分数或小数，就不是最简二次根式；二次根式的被开方数不能含有开方开得尽的因数或因式．

2.【答案】B 

【解析】解：A、因为，故不能构成直角三角形，故此选项不符合要求；
B、因为，能构成直角三角形，故此选项符合要求；
C、因为，故不能构成直角三角形，故此选项不符合要求；
D、因为，故不能构成直角三角形，故此选项不符合要求；
故选：
由勾股定理的逆定理可得，只要验证两较短边的平方和等于最长边的平方即可．
本题考查勾股定理的逆定理的应用，如果三角形的三边长a，b，c满足，那么这个三角形就是直角三角形．

3.【答案】C 

【解析】解：A、，故该选项不符合题意；
B、，故该选项不符合题意；
C、，故该选项符合题意；
D、，故该选项不符合题意；
故选：
根据二次根式的加、减、乘、除法的运算法则逐一进行计算即可作出判断．
本题考查了二次根式的运算，熟练掌握和运用二次根式的运算法则是解题的关键．

4.【答案】C 

【解析】解：四边形ABCD是平行四边形，
，
，
，
，

，
，
故选：
根据平行四边形的性质得到，利用勾股定理求出OB即可．
此题考查了平行四边形的性质，勾股定理，正确掌握平行四边形的性质是解题的关键．

5.【答案】D 

【解析】解：A、对角线垂直的平行四边形是菱形，正确，故不符合题意；
B、对角线相等的平行四边形是矩形，正确，故不符合题意；
C、菱形的面积等于对角线乘积的一半，正确；故不符合题意；
D、对角线互相垂直平分且相等的四边形是正方形，故选项错误，故符合题意．
故选：
根据矩形、菱形、正方形的判定定理即可作出判断．
本题考查了矩形、菱形、正方形的判定定理，正确理解定理是关键．

6.【答案】B 

【解析】解：这组数据的平均数、方差和标准差都与第5个数有关，而这组数据的中位数为36与46的平均数，与第5个数无关．
故选：
利用平均数、中位数、方差和标准差的定义对各选项进行判断．
本题考查了方差：它也描述了数据对平均数的离散程度．也考查了中位数、平均数和众数的概念．

7.【答案】A 

【解析】解：设，
、C的坐标分别为、，
，，，，，
，，
，
，，
，，
，
整理得，
把代入得，
，
，
，
矩形OMBN的面积为，
故选：
设，根据，，利用距离公式列方程求出mn的值即可．
本题考查勾股定理，解题的关键是根据坐标构造直角三角形利用勾股定理列方程计算．

8.【答案】A 

【解析】解：从图象得到，当时，的图象对应的点在函数的图象上面，
不等式的解集为：
故选：
函数和的图象交于点，求不等式的解集，就是看函数在什么范围内的图象对应的点在函数的图象上面．
本题考查了一次函数与不等式组的关系及数形结合思想的应用．解决此类问题关键是仔细观察图形，注意几个关键点交点、原点等，做到数形结合．

9.【答案】D 

【解析】解：四边形ABCD是正方形，
，，，
，
，
将正方形ABCD沿直线DF折叠，点C落在对角线BD上的点E处，
，，
，，
，
在与中
，
≌，
，
故选：
根据正方形的性质得到，，，求得，得到，根据折叠的性质得到，，求得，根据全等三角形的性质即可得到结论．
本题考查了翻折变换折叠问题，全等三角形的判定和性质，正方形的性质，正确的识别图形是解题的关键．

10.【答案】A 

【解析】解：作轴，作于点D，如右图所示，
由已知可得，，，，，，点C的纵坐标是y，
轴，
，
，
，
，
在和中，
，
≌，
，
，
点C到x轴的距离为y，点D到x轴的距离等于点A到x轴的距离1，

故选：
根据题意作出合适的辅助线，可以先证明和的关系，即可建立y与x的函数关系，从而可以得到哪个选项是正确的．
本题考查动点问题的函数图象，解题的关键是明确题意，建立相应的函数关系式，根据函数关系式判断出正确的函数图象．

11.【答案】且 

【解析】【分析】
本题考查了函数自变量的范围，根据分式有意义，二次根式有意义解答即可．
【解答】
解：由题意得，
解得：且

12.【答案】2 

【解析】解：是一次函数，
，，
解得，
故答案为：
一般地，形如、b是常数的函数，叫做一次函数．
本题主要考查了一次函数的定义，关键是掌握一次函数解析式的结构特征：；自变量的次数为1；常数项b可以为任意实数．

13.【答案】5 5 

【解析】解：数据1，4，a，9，6，5的平均数为5，
，
解得：，
把这些数从小到大排列为：1，4，5，5，6，9，
则中位数是；
出现了2次，出现的次数最多，
众数是5；
故答案为：5，
根据平均数的计算公式先求出a的值，再根据中位数和众数的定义即可得出答案．
此题考查了平均数、众数和中位数，中位数是将一组数据从小到大或从大到小重新排列后，最中间的那个数最中间两个数的平均数，叫做这组数据的中位数，众数是一组数据中出现次数最多的数．

14.【答案】10或 

【解析】解：①当6和8为直角边时，
第三边长为；
②当8为斜边，6为直角边时，
第三边长为
故答案为：10或
分情况考虑：当较大的数8是直角边时，根据勾股定理求得第三边长是10；当较大的数8是斜边时，根据勾股定理求得第三边的长是
一定要注意此题分情况讨论，很容易漏掉一些情况没考虑．

15.【答案】、或 

【解析】解：令一次函数中，则，
解得：，
点A的坐标为；
令一次函数中，则，
点B的坐标为
设点M的坐标为，则，，，
是以AB为腰的等腰三角形分两种情况：
①，即，
解得：，或，
此时点M的坐标为或；
②，即，
解得：，或舍去，
此时点M的坐标为
综上可知点M的坐标为、或
故答案为、或
分别令一次函数中、，求出点A、B的坐标，设出点M的坐标，根据两点间的距离公式表示出AB、AM和BM的长度，分与两种情况来考虑，由此可得出关于m的方程，解关于m的方程即可得出结论．
本题考查了一次函数图象上点的坐标特征以及等腰三角形的性质，解题的关键是分与两种情况来考虑．

16.【答案】 

【解析】解：矩形ABCD，
，，，
，
由折叠得，，
，
，
由折叠得，
，，
，
在中，，
在中，，
，
故答案为：
由矩形的性质，折叠轴对称的性质，可求出，由勾股定理求出AB，AC，进而求出OA即可．
本题考查矩形的性质、折叠轴对称的性质，勾股定理等知识，根据图形，求出线段AB、AC的长是得出答案的关键．

17.【答案】解：原式

 

【解析】先利用完全平方公式和平方差公式计算，然后合并即可．
本题考查了二次根式的混合运算：熟练掌握二次根式的性质、二次根式的乘法法则、乘法公式和零指数幂是解决问题的关键．

18.【答案】解：

 

【解析】本题考查了二次根式的加减运算，二次根式的加减运算，先化为最简二次根式，再将被开方数相同的二次根式进行合并．合并同类二次根式的实质是合并同类二次根式的系数，根指数与被开方数不变．
先化为最简二次根式，再将被开方数相同的二次根式进行合并．

19.【答案】解：在中，，，，
，
此人以的速度收绳，5s后船移动到点D的位置，
，
，
船向岸边移动了，
答：船向岸边移动了 

【解析】先利用勾股定理求出AB的长度，然后根据题意求出CD的长度，进而即可求出AD的长即得解答．
本题主要考查勾股定理的应用，掌握勾股定理是解题的关键．

20.【答案】证明：四边形ABCD是平行四边形，
，
，
点E是CD边的中点，
，
又，
≌，
，
，
，
，
，
，
平分
解：，，
，
，
，
，
≌，
，
 

【解析】证≌，根据全等三角形的性质结合垂直平分线的性质即可求证；
由即可求解．
本题考查了平行四边形的性质、全等三角形的判定与性质等知识点．掌握相关结论进行几何推导是解题关键．

21.【答案】4 120 

【解析】解：根据题意得：，
，
故答案为：4；120；
设甲车的解析式为，
将点，代入解析式，
可得：，
解得：，
甲车的函数关系式为：；
①当时，设，
将点代入解析式得：，
解得：，
；
②当时，设，
将点，代入解析式得：，
解得：，
，
综上可得：乙车的函数解析式为：；
根据题意，可知：当行驶的时间为时，甲车到达B地，
由可知：当乙车行驶时，其函数解析式为：，
当时，，
当甲车到达B地时，乙车距B地的路程为
根据相遇后“乙车立即以原速原路返回到B地”，可求m；根据甲车的行驶情况可求n；
首先根据待定系数法求出甲车的函数解析式，然后分两种情况：当时和当时，根据待定系数法求出乙车的函数解析式即可；
根据题意，得出当行驶的时间为时，甲车到达B地，再根据得出当乙车行驶时，其函数解析式为：，然后把代入函数解析式，计算即可得出答案．
本题考查了利用待定系数法求函数解析式、从函数图象获取信息、有理数的混合运算的应用，从函数图象得出正确信息是解题的关键．

22.【答案】解：，

补全统计图为：

平均数；
四月份“读书量”为5本的学生人数人，
答：四月份“读书量”为5本的学生人数为120人． 

【解析】【分析】
本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．

根据统计图可知众数为3；
根据平均数计算公式求解；

用总数乘以样本中读书量”为5本的学生的百分率即可

【解答】
解：根据统计图可知众数为3，
故答案为3；
补全统计图见答案；
见答案，

23.【答案】解：四边形ABCD是矩形，理由如下：
四边形ABCD是平行四边形，
，，
是等腰直角三角形，
，，
，
，
，
平行四边形ABCD是矩形；
平行四边形ABCD是矩形，
，，，
，
，
，
，
，
，
在和中，，
≌，
，，
，
，
，
，
 

【解析】由平行四边形的性质和等腰直角三角形的性质，得出，则，得出平行四边形ABCD是矩形；
由SAS证得≌，得出，，证明，由等腰直角三角形的性质与勾股定理即可得出结果．
本题考查了平行四边形的性质、矩形的判定与性质、等腰直角三角形的性质、全等三角形的判定与性质、勾股定理等知识；熟练掌握矩形的判定与性质、证明≌是解题的关键．

24.【答案】解：由题意，甲团队不超过50人，则乙团队x人满足
，
，随x的增大而减小，
当时，W有最大值，即为元，
两队联合购票费用为元，
两队联合购票比分别购票最多可节约元

由题意，得
当时，W有最大值
两队联合购票费用是，
根据题意，列方程
解得 

【解析】根据甲、乙两团队分别购买门票的费用之和，列出关系式即可；
根据题意构建方程即可解决问题；
本题考查一次函数的应用，一元一次方程等知识，解题的关键是理解题意，学会构建一次函数，利用一次函数的性质解决最值问题，属于中考常考题型．