






2024届人教A版高考数学一轮复习二项分布与正态分布课件
展开P(B|A)+P(C|A)
3. 独立重复试验与二项分布(1)独立重复试验 定义:一般地,在相同条件下重复做n次试验称为n次独立重复试验.计算公式:若用Ai(i=1,2,3,…,n)表示第i次试验的结果,则这n个事件同时发生的概率P(A1A2…An)=P(A1)·P(A2)…P(An).(2)二项分布定义:一般地,在n次独立重复试验中,设事件A发生的次数为X,在每次试验中事件A发生的概率为p,此时称随机变量X服从二项分布,记作⑥X~B(n,p),并称p为成功的概率.
计算公式:在n次独立重复试验中,事件A恰好发生k次的概率为P(X=k)= ,k=0,1,2,…,n.二项分布的期望与方差:若随机变量X服从二项分布,即X~B(n,p),则E(X)=np,D(X)= .名师提醒 1.独立重复试验的条件(1)每次试验在相同条件下可重复进行;(2)每次试验是相互独立的;(3)每次试验都只有两种结果,即事件要么发生,要么不发生.
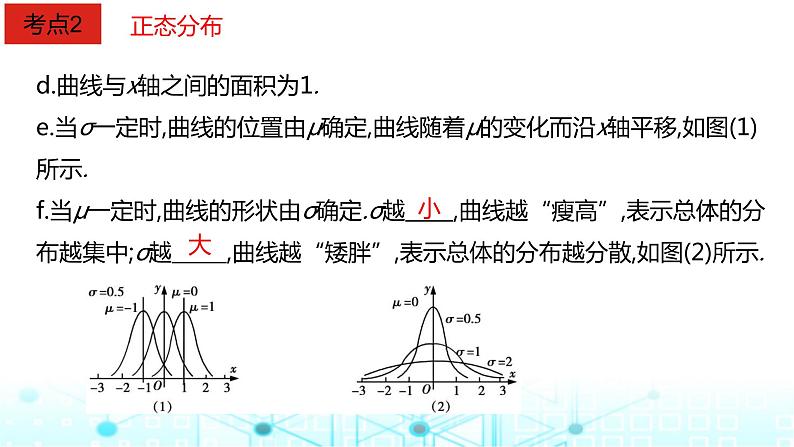
d.曲线与x轴之间的面积为1.e.当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移,如图(1)所示.f.当μ一定时,曲线的形状由σ确定.σ越 ,曲线越“瘦高”,表示总体的分布越集中;σ越 ,曲线越“矮胖”,表示总体的分布越分散,如图(2)所示.
(2)正态分布的三个常用数据a. P(μ-σ
1.典例 [2021安徽师大附中5月模拟]设10件产品中有4件不合格,从中任意选取2件,则在所选取的产品中发现有一件是不合格品时,另一件也是不合格品的概率是 .
解析 记事件A为“选取的两件产品中发现有一件是不合格品”,事件B为“另一件是不合格品”,则AB为“两件都是不合格品”.
方法技巧 1.求条件概率的三种方法
2.条件概率的判断依据对条件概率问题的判断主要依据题目中出现的“已知”“在…前提下(条件下)”等字眼.若题目中没有出现上述字眼,但已知事件的发生影响了所求事件的概率,一般也认为是条件概率问题.
2.变式 [2021广东佛山三模]设某种动物由出生算起,活到20岁的概率是0.8,活到25岁的概率是0.4.现有一个20岁的这种动物,它能活到25岁的概率是 .
角度1 相互独立事件的判断
3.典例 [2021新高考卷Ⅰ]有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回地随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则( )A.甲与丙相互独立 B.甲与丁相互独立C.乙与丙相互独立 D.丙与丁相互独立
角度2 相互独立事件的概率的求法
4.典例 [2019全国卷Ⅱ][理]11分制乒乓球比赛,每赢一球得1分,当某局打成10∶10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10∶10平后,甲先发球,两人又打了X个球该局比赛结束.(1)求P(X=2);(2)求事件“X=4且甲获胜”的概率.
解析 (1)“X=2”包含的事件为“甲连赢两球”或“乙连赢两球”.因此P(X=2)=0.5×0.4+(1-0.5)×(1-0.4)=0.5.(2)“X=4且甲获胜”包含的事件为“前两球甲、乙各得1分,后两球均为甲得分”.因此所求概率为[0.5×(1-0.4)+(1-0.5)×0.4]×0.5×0.4=0.1.
方法技巧相互独立事件的概率的求法(1)直接法:利用相互独立事件的概率乘法公式直接求解.(2)间接法:正面计算较烦琐(如求用“至少”表述的事件的概率)或难以入手时,可从其对立事件入手计算.与相互独立事件A,B有关的概率的计算公式如下表:
5.变式 [2019全国卷Ⅰ][理]甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4∶1获胜的概率是 .
独立重复试验与二项分布
方法技巧1.利用二项分布解决实际问题的关键是建立二项分布模型,随机变量X服从二项分布的依据:①试验为n次独立重复试验;②随机变量X是在这n次独立重复试验中某事件发生的次数.若X~B(n,p),则利用公式E(X)=np,D(X)=np(1-p)求期望、方差,可减少计算量.2.有些随机变量虽不服从二项分布,但与之具有线性关系的另一随机变量服从二项分布,这时,可以应用均值与方差的性质求解,即利用E(ax+b)=aE(x)+b,D(ax+b)=a2D(x)求解.
8.变式 [2018全国卷Ⅰ][理]某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品做检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件做检验,再根据检验结果决定是否对余下的所有产品做检验.设每件产品为不合格品的概率都为p(0
(2)由(1)知,p0=0.1,所以p=0.1.(i)令Y表示余下的180件产品中的不合格品的件数,依题意知Y~B(180,0.1),X=20×2+25Y,即X=40+25Y.所以E(X)=E(40+25Y)=40+25E(Y)=40+25×180×0.1=490.(ii)如果对这箱余下的产品做检验,那么这一箱产品所需要的检验费为400元.由于E(X)>400,故应该对这箱余下的所有产品做检验.
9.典例 [2021新高考卷Ⅱ]某物理量的测量结果服从正态分布N(10,σ2),则下列结论中不正确的是 ( )A.σ越小,该物理量一次测量结果落在(9.9,10.1)内的概率越大B.该物理量一次测量结果大于10的概率为0.5C.该物理量一次测量结果小于9.99的概率与大于10.01的概率相等D.该物理量一次测量结果落在(9.9,10.2)内的概率与落在(10,10.3)内的概率相等
解析 设该物理量一次测量结果为X,对于A,σ越小,说明数据越集中在10附近,所以X落在(9.9,10.1)内的概率越大,所以选项A正确;对于B,根据正态曲线的对称性可得,P(X>10)=0.5,所以选项B正确;对于C,根据正态曲线的对称性可得,P(X>10.01)=P(X<9.99),所以选项C正确;对于D,根据正态曲线的对称性可得,P(9.9
思维拓展对于正态分布N(μ,σ2),由直线x=μ是正态曲线的对称轴知:(1)P(x≥μ)=P(x<μ)=0.5;(2)对任意的a,有P(X<μ-a)=P(X>μ+a);(3)P(X
解析 (1)抽取的一个零件的尺寸在(μ-3σ,μ+3σ)之内的概率约为0.997 3,从而零件的尺寸在(μ-3σ,μ+3σ)之外的概率约为0.002 7,故X~B(16,0.002 7).因此P(X≥1)=1-P(X=0)=1-0.997 316≈0.042 3.X的数学期望E(X)=16×0.002 7=0.043 2.(2)(i)如果生产状态正常,一个零件的尺寸在(μ-3σ,μ+3σ)之外的概率只有0.002 7,一天内抽取的16个零件中,出现尺寸在(μ-3σ,μ+3σ)之外的零件的概率只有0.042 3,发生的概率很小.
概率与其他学科的综合问题
11.典例 如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是p,电流能通过T4的概率是0.9,电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999.则:(1)p= ;(2)电流能在M与N之间通过的概率为 .
解析 记Ai表示事件“电流能通过Ti”,i=1,2,3,4,A表示事件“T1,T2,T3中至少有一个能通过电流”,B表示事件“电流能在M与N之间通过”.
概率与其他知识的综合问题
13.典例 [2021新高考卷Ⅱ]一种微生物群体可以经过自身繁殖不断生存下来,设一个这种微生物为第0代,经过一次繁殖后为第1代,再经过一次繁殖后为第2代……该微生物每代繁殖的个数是相互独立的且有相同的分布列,设X表示1个微生物个体繁殖下一代的个数,P(X=i)=pi(i=0,1,2,3).(1)已知p0=0.4,p1=0.3,p2=0.2,p3=0.1,求E(X);(2)设p表示该种微生物经过多代繁殖后临近灭绝的概率,p是关于x的方程p0+p1x+p2x2+p3x3=x的一个最小正实根,求证:当E(X)≤1时,p=1,当E(X)>1时,p<1;(3)根据你的理解说明(2)问结论的实际含义.
解析 (1)由题意,P(X=0)=0.4,P(X=1)=0.3,P(X=2)=0.2,P(X=3)=0.1,∴X的分布列为E(X)=0×0.4+1×0.3+2×0.2+3×0.1=1.(2)记f(x)=p3x3+p2x2+(p1-1)x+p0,由题知,p为f(x)=0的实根,由p0=1-p1-p2-p3,得f(x)=p3(x3-1)+p2(x2-1)+p1(x-1)-(x-1)=(x-1)[p3x2+(p3+p2)x+p3+p2+p1-1].
记g(x)=p3x2+(p3+p2)x+p3+p2+p1-1,则g(1)=3p3+2p2+p1-1=E(X)-1,g(0)=p3+p2+p1-1=-p0<0.当E(X)≤1时,g(1)≤0,易知g(x)在(0,1)上单调递增,∴当x∈(0,1)时,g(x)=0无实根.∴f(x)=0在(0,1]上有且仅有一个实根,即p=1,∴当E(X)≤1时,p=1.
当E(X)>1时,g(1)>0,又g(0)<0,g(x)的图象开口向上,∴g(x)=0在(0,1)上有唯一实根p',∴f(x)=0的最小正实根p=p'∈(0,1),∴当E(X)>1时,p<1.(3)E(X)≤1,表示1个微生物个体繁殖下一代的个数不超过自身个数,种群数量无法维持稳定或正向增长,多代繁殖后将面临灭绝,所以p=1.E(X)>1,表示1个微生物个体可以繁殖下一代的个数超过自身个数,种群数量可以正向增长,所以面临灭绝的可能性小于1.
14.变式 [2019全国卷Ⅰ][理]为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
(1)求X的分布列.(2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5, β=0.8.(i)证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列.(ii)求p4,并根据p4的值解释这种试验方案的合理性.
解析(1)X的所有可能取值为-1,0,1.P(X=-1)=(1-α)β,P(X=0)=αβ+(1-α)(1-β),P(X=1)=α(1-β).所以X的分布列为(2)(i)由(1)得a=0.4,b=0.5,c=0.1.因此pi=0.4pi-1+0.5pi+0.1pi+1(i=1,2,…,7),故0.1(pi+1-pi)=0.4(pi-pi-1),即pi+1-pi=4(pi-pi-1).
人教A版高考数学一轮总复习第10章第6节二项分布、超几何分布与正态分布教学课件: 这是一份人教A版高考数学一轮总复习第10章第6节二项分布、超几何分布与正态分布教学课件,共60页。
人教A版高考数学一轮总复习课时质量评价61二项分布、超几何分布与正态分布习题课件: 这是一份人教A版高考数学一轮总复习课时质量评价61二项分布、超几何分布与正态分布习题课件,共35页。PPT课件主要包含了A组全考点巩固练,B组新高考培优练,答案BC等内容,欢迎下载使用。
人教B版高考数学一轮总复习61二项分布、超几何分布与正态分布习题课件: 这是一份人教B版高考数学一轮总复习61二项分布、超几何分布与正态分布习题课件,共38页。PPT课件主要包含了A组全考点巩固练,B组新高考培优练等内容,欢迎下载使用。












