






2024届人教A版高考数学一轮复习函数的基本性质课件
展开函数的单调性与最值
f(x1)
注意 1.函数的单调性定义中的x1,x2有三个特征:一是任意性;二是有大小,即x1
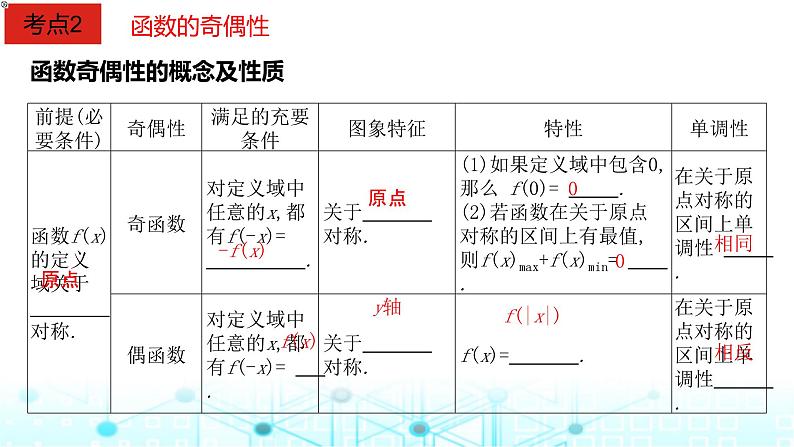
函数奇偶性的概念及性质
注意 (1)只有函数在x=0处有定义时,f(0)=0才是f(x)为奇函数的必要非充分条件;(2)既是奇函数又是偶函数的函数只有一种类型,即f(x)=0,x∈D,其中定义域D是关于原点对称的非空数集.
思维拓展 (1)若函数y=f(x+a)是偶函数,则函数y=f(x)的图象关于直线x=a对称,f(x+a)=f(-x+a).(2)若函数y=f(x+b)是奇函数,则函数y=f(x)的图象关于点(b,0)中心对称,f(x+b)+f(-x+b)=0.
1.周期函数对于函数y=f(x),如果存在一个非零常数T,使得当x取定义域内的任何值时,都有 ,那么就称函数y=f(x)为周期函数,称T为这个函数的周期. 2.最小正周期如果在周期函数f(x)的所有周期中存在最小的正数,那么这个最小的正数就叫作f(x)的 正周期.
注意 并不是所有的周期函数都有最小正周期,如f(x)=5.
f(x+T)=f(x)
确定函数的单调性(单调区间)
解析 (1)(图象法)如图,在坐标系中分别画出A,B,C,D四个选项中的函数的大致图象,即可判断D项符合题意.(也可根据基本初等函数的性质,直接判断)
(2)(复合法)由x2-2x-8>0,得x<-2或x>4.因此,函数f(x)=ln(x2-2x-8)的定义域是(-∞,-2)∪(4,+∞).(先求函数f(x)的定义域)易知函数y=x2-2x-8在(-∞,-2)上单调递减,在(4,+∞)上单调递增,函数y=ln t为(0,+∞)上的增函数,由复合函数的单调性知,f(x)=ln(x2-2x-8)的单调递增区间是(4,+∞).故选D.
(3)解法一(导数法) f'(x)=a(x-1)-ax(x-1)2=-a(x-1)2.当a>0时,f '(x)<0,函数f(x)在(-1,1)上单调递减;当a<0时,f '(x)>0,函数f(x)在(-1,1)上单调递增.解法二(定义法) 设-1
方法技巧 利用函数的单调性比较大小的方法比较函数值的大小时,应先将自变量的值转化到同一个单调区间内,再利用函数的单调性求解.
3.典例 [2017全国卷Ⅰ][理]函数f(x)在(-∞,+∞)上单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是 ( )A.[-2,2]B.[-1,1]C.[0,4]D.[1,3]
解析 ∵函数f(x)为奇函数,且f(1)=-1,∴f(-1)=-f(1)=1,由-1≤f(x-2)≤1,得f(1)≤f(x-2)≤f(-1),(将常数转化为函数值)又函数f(x)在(-∞,+∞)上单调递减,∴-1≤x-2≤1,∴1≤x≤3.故选D.
方法技巧 利用函数的单调性求解或证明不等式的策略(1)将不等式转化为f(x1)>f(x2)的形式;(2)根据函数f(x)的单调性“脱去”函数符号“f ”化为形如“x1>x2”或“x1
4.典例 [2020新高考卷Ⅱ]已知函数f(x)=lg(x2 -4x-5)在(a,+∞)上单调递增,则a的取值范围是 ( )A.(-∞,-1]B.(-∞,2]C.[2,+∞)D.[5,+∞)
解析 由x2-4x-5>0,解得x>5或x<-1,所以函数f(x)的定义域为(-∞,-1)∪(5,+∞).因为函数y=x2-4x-5在(5,+∞)上单调递增,在(-∞,-1)上单调递减,所以函数f(x)=lg(x2-4x-5)在(5,+∞)上单调递增,所以a≥5,故选D.
方法技巧 已知函数的单调性求参数的取值范围的方法根据函数的单调性构建含参数的方程(组)或不等式(组)进行求解,或先得到图象的升降情况,再结合图象求解.
注意 若分段函数是单调函数,则不仅要各段上函数单调性一致,还要在整个定义域内单调,即要注意衔接点处的函数值大小.
求函数的最值(值域)
方法技巧 求函数最值(值域)的方法(1)单调性法:先确定函数的单调性,再由单调性求出最值(值域).(2)图象法:先作出函数的图象,再观察其最高点、最低点求出最值(值域),若函数的解析式的几何意义较明显,如距离、斜率等,可用数形结合法求解.(3)基本不等式法:先对解析式变形,使之具备“一正二定三相等”的条件后用基本不等式求最值(值域).(4)导数法:先求出导函数,然后求出给定区间上的极值,再结合端点值,求出最值(值域).适用于三次函数、分式函数及含ex,ln x,sin x,cs x等结构的组合函数,且f '(x)可求.
方法技巧 判断函数奇偶性的方法(1)定义法
(3)性质法在公共定义域内有奇函数±奇函数=奇函数,偶函数±偶函数=偶函数,奇函数×奇函数=偶函数,偶函数×偶函数=偶函数,奇函数×偶函数=奇函数.
注意 (1)函数定义域关于原点对称是函数具有奇偶性的前提条件.(2)对于分段函数奇偶性的判断,要分段判断f(-x)=f(x)或f(-x)=-f(x)是否成立,只有当所有区间都满足相同关系时,才能判断该分段函数的奇偶性.
9.变式 [新课标全国Ⅰ][理]设函数f(x),g(x)的定义域都为R,且 f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( )A. f(x)g(x)是偶函数 B. f(x)|g(x)|是奇函数C.|f(x)|g(x)是奇函数 D.|f(x)g(x)|是奇函数
解析 因为f(x)为奇函数,g(x)为偶函数,所以f(x)g(x)为奇函数,f(x)|g(x)|为奇函数,|f(x)|g(x)为偶函数,|f(x)g(x)|为偶函数,故选B.
方法技巧 函数奇偶性的应用类型及解题策略
函数周期性的判断及应用
12.典例 [2022豫北名校联考]已知y=f(x)为奇函数且对任意x∈R,都有f(x+2)=-f(x),若当x∈[0,2]时,f(x)=2x+a,则f(2 022)= ( )A.4B.3C.2D.1
解析 因为f(x)是奇函数且对任意x∈R,都有f(x+2)=-f(x),所以f(x+4)=-f(x+2)=f(x),所以函数f(x)是周期为4的周期函数.由奇函数性质可知,f(0)=20+a=1+a=0,a=-1,所以f(2 022)=f(505×4+2)=f(2)=22-1=3,故选B.
方法技巧 1.判断函数的周期性时,只需证明f(x+T)=f(x)(T≠0)便可证明函数是周期函数,且周期为T.2.根据函数的周期性,可以由函数的局部性质得到函数的整体性质,周期性与奇偶性都具有将未知区间上的问题转化到已知区间的功能.
函数性质的综合应用
14.典例 (1)[2020新高考卷Ⅰ]若定义在R上的奇函数f(x)在(-∞,0)上单调递减,且f(2)=0,则满足xf(x-1)≥0的x的取值范围是 ( ) A.[-1,1]∪[3,+∞) B.[-3,-1]∪[0,1]C.[-1,0]∪[1,+∞) D.[-1,0]∪[1,3](2)[2018全国卷Ⅱ][理]已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x).若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=( )A.-50 B.0C.2D.50
解析 (1)解法一 由题意知f(x)在(-∞,0),(0,+∞)上单调递减,且f(-2)=f(2)=f(0)=0.当x>0时,令f(x-1)≥0,得0≤x-1≤2,∴1≤x≤3;当x<0时,令f(x-1)≤0,得-2≤x-1≤0,∴-1≤x≤1,又x<0,∴-1≤x<0;当x=0时,显然符合题意.综上,原不等式的解集为[-1,0]∪[1,3],选D.解法二 当x=3时,f(3-1)=0,符合题意,排除B;当x=4时,f(4-1)=f(3)<0,此时不符合题意,排除A,C.选D.(2)解法一 ∵f(x)是定义域为(-∞,+∞)的奇函数,∴f(-x)=-f(x),且f(0)=0.∵f(1-x)=f(1+x),∴f(-x)=f(2+x),∴f(2+x)=-f(x),
∴f(2+x)=-f(x),∴f(4+x)=-f(2+x)=f(x),∴f(x)是周期函数,且一个周期为4,∴f(4)=f(0)=0,f(2)=f(1+1)=f(1-1)=f(0)=0,f(3)=f(1+2)=f(1-2)=-f(1)=-2,∴f(1)+f(2)+f(3)+f(4)+…+f(50)=12×0+f(49)+f(50)=f(1)+f(2)=2.故选C.解法二 因为函数f(x)满足f(1-x)=f(1+x),可知f(x)的图象关于直线x=1对称.又f(x)是定义域为(-∞,+∞)的奇函数,所以f(0)=0.已知f(1)=2,计算可得:
f(2)=f(0)=0,f(3)=f(-1)=-f(1)=-2,f(4)=f(-2)=-f(2)=0,f(5)=f(-3)=-f(3)=2,f(6)=f(-4)=-f(4)=0,f(7)=f(-5)=-f(5)=-2,f(8)=f(-6)=-f(6)=0,……所以f(1)+f(2)+f(3)+…+f(49)+f(50)=(2+0-2+0)×12+2+0=2.故选C.
函数奇偶性的拓广性质及应用
性质1 若函数f(x)是奇函数,且g(x)=f(x)+c,则必有g(-x)+g(x)=2c.证明 由于函数f(x)是奇函数,所以f(-x)=-f(x),所以g(-x)+g(x)=f(-x)+c+f(x)+c=2c.
16.典例 (1)[2022长春市质量监测]已知函数f(x)=x3-3x-2,若f(a)=4,则f(-a)=( )A.-2B.-4C.-6D.-8(2)对于函数f(x)=asin x+bx+c(其中a,b∈R,c∈Z),选取a,b,c的一组值分别计算f(1)和f(-1),所得出的正确结果不可能是( )A.4和6B.3和1 C.2和4D.1和2
解析 (1)令g(x)=x3-3x,则f(x)=g(x)-2,因为g(-x)=-g(x),所以g(x)是奇函数,所以f(a)+f(-a)=-4,由f(a)=4,可得f(-a)=-8.(2)设g(x)=asin x+bx,则f(x)=g(x)+c,且函数g(x)为奇函数.注意到c∈Z,所以f(1)+f(-1)=2c为偶数.结合选项可知只有D项不满足.
点评 解题关键在于观察函数的结构,构造出一个奇函数.
性质2 已知函数f(x)是定义在区间D上的奇函数,则对任意的x∈D,都有f(x)+f(-x)=0.特别地,若奇函数f(x)在D上有最值,则f(x)max+f(x)min=0,且若0∈D,则f(0)=0.
17.典例 [2022西安复习检测]函数f(x)=(x2-1)(ex-e-x)+x+1在区间[-2,2]上的最大值与最小值分别为M,N,则M+N的值为 .
解析 设g(x)=(x2-1)(ex-e-x)+x,则f(x)=g(x)+1.因为g(-x)=(x2-1)(e-x-ex)-x=-g(x),且g(x)的定义域关于原点对称,所以g(x)是奇函数.由奇函数图象的对称性知g(x)max+g(x)min=0,∴M+m=[g(x)+1]max+[g(x)+1]min=2+g(x)max+g(x)min=2.
点评 若定义在区间D上的函数f(x)关于点(0,b)对称,则对任意x∈D,有f(x)+f(-x)=2b.
性质3 若函数f(x)为偶函数,则f(x)=f(|x|).证明 当x≥0时,|x|=x,所以f(|x|)=f(x);当x<0时,f(|x|)=f(-x),由于函数f(x)为偶函数,所以f(-x)=f(x),故f(|x|)=f(x).综上,若函数f(x)为偶函数,则f(x)=f(|x|).
2024届人教A版高考数学一轮复习函数与方程课件: 这是一份2024届人教A版高考数学一轮复习函数与方程课件,共30页。PPT课件主要包含了函数的零点,考点1,实数x,零点存在定理,连续不断,考点2,考向扫描,考向1,判断函数的零点个数,考向2等内容,欢迎下载使用。
2024届人教A版高考数学一轮复习函数的图象课件: 这是一份2024届人教A版高考数学一轮复习函数的图象课件,共33页。PPT课件主要包含了函数的图象,fx-a,fx-h,yf-x,y-f-x,Afx,考向扫描,考向1,函数图象的应用,考向2等内容,欢迎下载使用。
数学必修 第一册3.2 函数的基本性质优秀ppt课件: 这是一份数学必修 第一册3.2 函数的基本性质优秀ppt课件,共38页。












