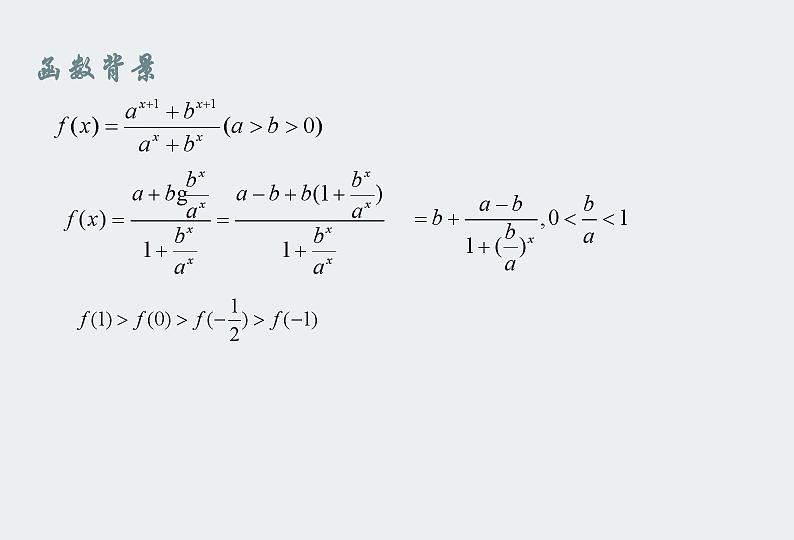
2025版高考一轮数学总复习 (通用版)教学课件

这是一份2025版高考一轮数学总复习 (通用版)教学课件，文件包含4函数与导数高考试题分析及备考策略pptx、6立体几何考情分析与备考建议pptx、7解析几何pptx、3三角函数与平面向量考情分析与备考策略pptx、5数列求通项与求和pptx、题型一多项选择题的特点及求解策略pptx、1集合的概念与运算pptx、题型四结构不良型试题的特点及求解策略pptx、8概率与统计pptx、题型三开放探究题的特点及求解策略pptx、题型二阅读理解题的特点及求解策略pptx、2基本不等式pptx等12份课件配套教学资源，其中PPT共462页， 欢迎下载使用。

明确要求——《高中数学课程标准》
目录 CONTENTS
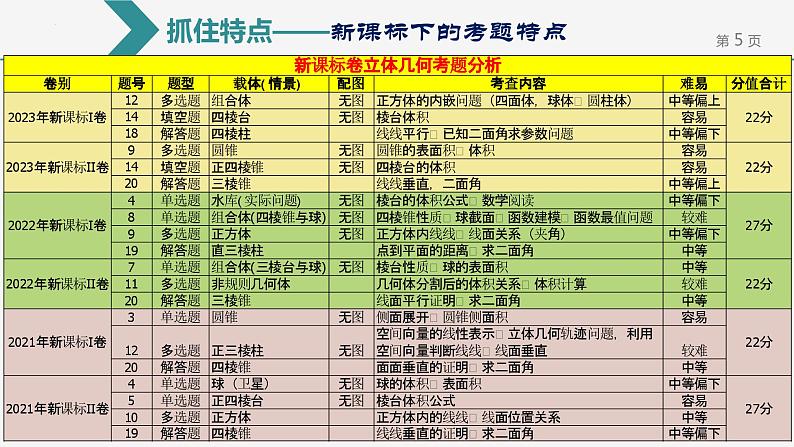
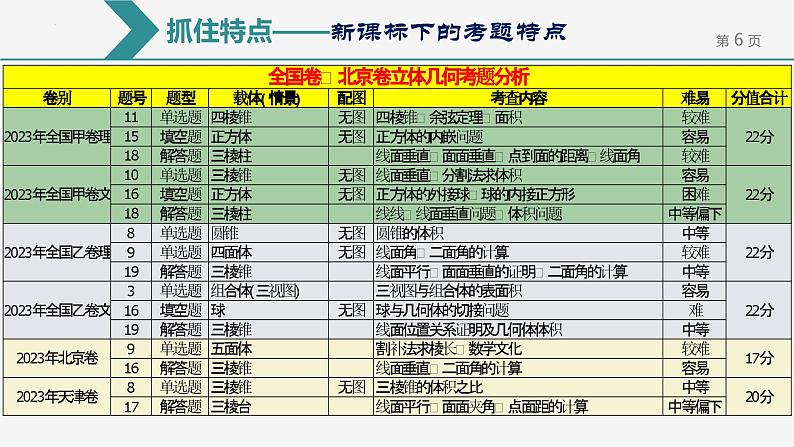
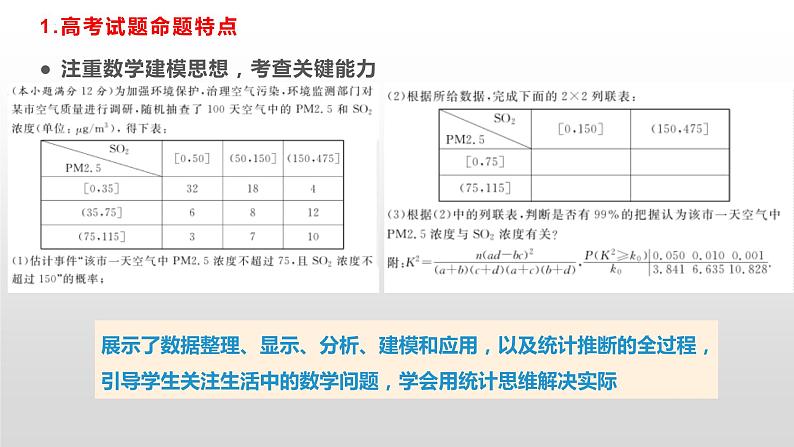
抓住特点——新课标下的考题特点
强化重点——新形势下的考查重点
备考建议——新课标下的备考建议
立体几何研究现实世界中物体的形状、大小与位置关系。（1）本单元的学习，可以帮助学生以长方体为载体，认识和理解空间点、直线、平面的位置关系；（2）用数学语言表述有关平行、垂直的性质与判定，并对某些结论进行论证；（3）了解一些简单几何体的表面积与体积的计算方法；（4）运用直观感知、操作确认、推理论证、度量计算等认识和探索空间图形的性质，建立空间观念。 内容包括：基本立体图形、基本图形位置关系、*几何学的发展。
（1）立体几何初步的教学重点是帮助学生逐步形成空间观念； （2）帮助学生认识空间几何体的结构特征，进一步掌握在平面上表示空间图形的方法和技能； （3）学会用准确的数学语言表达与平行、垂直有关的定理； （4）鼓励学生灵活选择运用向量方法与几何方法，从不同角度解决立体几何问题(如距离问题)，通过对比体会向量方法的优势。
考点覆盖全面，题型一应俱全；
知识点重复考查，背景新颖；
解答题考查全面，重点突出；
知识融汇贯通，情境新颖多样；
特点1：考点覆盖全面，题型一应俱全
（1）围绕空间几何体的基本结构和度量； （2）围绕点、线、面之间的位置关系； （3）围绕空间向量及其在立体几何中的应用。
新课标卷立体几何部分考点覆盖全面：
新课标卷立体几何单选题、多选题、填空题、解答题四种题型一应俱全。
无论是新课标卷还是全国卷，选择、填空题一般不会给出图形。这就要求学生需要具备读题画图的能力和空间想象能力。
特点2：知识点重复考查，背景新颖；
新课标卷中的小题基本上都是关于几何体的表面积体积问题，从不避讳，不怕重复，需要考生特别注意。
立体几何试题体现了“大稳定、小创新”的设计理念，强调数学的应用意识，关注对考生文化素养的考查。（如2023年北京卷中考查我国传统建筑造型“刍曹”）
特点3：解答题考查全面，重点突出
新课标卷I、II对立体几何解答题的考查角度基本一致，前一问主要考查空间中点、线、面的位置关系，将平行垂直关系作为考查的重点，后一问考查空间几何量（空间角）的计算。属于中等难度。
特点4：知识融汇贯通，情境新颖多样
近年来，高考试题不断创新，打破了以往试题命制的模式化，在知识考查难点的分布、题目设问方式的设计、试题排列顺序的变化等方面“反套路”。 从“小题”到“大题”新课标卷立体几何越来越活，融合了课程学习、探索创新、生活实践等情境问题，对学生的批判性思维能力，阅读理解能力，试题位置迁移信息整理能力，语言表达能力提出了更高要求。
特点4：知识交汇贯通，情境新颖多样
基础性综合性应用性创新性
核心价值学科素养关键能力必备知识
直观想象—空间几何体的表面积体积；
数学模型—球的切、接及截面问题；
数学运算—空间向量在立体几何中的应用；
逻辑推理—几何法在立体几何中的应用；
1.直观想象—空间几何体的表面积体积
空间几何体表面积和体积的考查实质要明确空间几何体的结构特征，并能进一步度量和计算长度、表面积、体积等。
(2023年新课标II卷第9题)
(2023年新课标II卷第14题)
(2023年新课标I卷第14题)
突出基础性考查，背景紧扣教材
常见方法：分割法、补体法、还台为锥法、等积变换法(如求三棱锥的体积可灵活变换顶点与底面)等,它们是计算一些不规则几何体体积常用的方法.
2.数学模型—球的切、接及截面问题
[解题思路]设 EF 的中点为 O ，则球O 的直径为 EF ，由于0点也是正方体的中心，所以O 点到各棱的距离均等于 OE ，故EF为直径的球的球面与该正方体的棱共有12个公共点。
【试题亮点】试题要求考生综合考察球与正方体的位置关系，正确认识图形中的直线与直线、直线与平面、平面与平面的位置关系，将问题转化为点到直线的距离的判断与计算问题．试题引导数学教学要重视数学抽象、直观想象等核心素养的培养，在教学中重视培养学生的想象力．考题重视基础知识、基本能力，考生通过直观想象、判断推理，可以发现解决问题的思路，以图形的对称性的特点去思考问题，可以较快地得到问题的答案，体现思维的灵活性．
结合图形，分析出临界位置
【试题亮点】试题将球的对称性与正方体的对称性结合起来设置问题情境，对考生的空间想象能力有一定的要求．试题要求考生在变化的过程中能抓住问题的本质，将问题转化为棱上的点与球心0的距离的范围问题，考查了考生数形结合、化归与转化等数学思想的运用能力．试题很好地体现了多想少算的命题设计的特点，体现了用数学的眼光分析问题的重要性，对引导教学改革，重视培养学生的数学核心素养有积极的导向作用．
利用：函数观点求立体几何的最值
[2022年新课标I卷第8题]
[考查目标]试题以考生熟悉的三棱锥和球为背景，给定球的半径和△ ABC 的形状，进而确定球心的位置，最后化归为研究平面 OSA 中等腰三角形高的问题． 试题考查三棱锥、球的基础知识，考查考生的空间想象、逻辑推理、运算求解等关键能力，考查考生理性思维、数学探索等学科素养，符合基础性、综合性、创新性的考查要求．
点评： 球与几何体的切接是高考的热点与难点,常作为客观题中的压轴题,考查热点是几何体的外接球,此类问题要求学生有较强的空间想象能力和准确的计算能力,才能顺利解答. 从实际来看,这部分知识是学生掌握最为模糊,看到就头疼的题目.分析原因,除了这类题目的入手确实不易之外,主要是学生没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理.
（1）熟悉基本的立体模型
(i). 几何体的外接球问题关键是确定球心位置,主要方法有： ① 将几何体还原或补为正方体或长方体,进而确定球心（补形找心）； ② 几何体的外接球球心一定在过底面的外心与底面垂直的直线上（垂线找心）； ③ 球心到各顶点的距离都相等（定义找心）； ④ 球心一定在外接球的直径上． (ii). 求解几何体外接球的半径主要是根据球的截面的性质,利用球的半径R、截面圆的半径r及球心到截面圆的距离d三者的关系R2＝r2＋d2求.使用频率非常高,考生一定要重视．
（2）掌握基本的解题方法
（3）几种特殊多面体的外接球和内切球半径
长方体：底面边长a,b、高为c，则外接球半径： (体对角线长度的一半)
正方体：棱长为a，则外接球半径： ，内切球半径： .
正三棱柱：高为h, 底面边长为a , 如图： 则外接球半径：
对棱相等的三棱锥：
四个面都是直角三角形的三棱锥：
三条侧棱两两垂直的三棱锥（墙角模型）：
正四面体：
（4）关注其它几何体的截面问题
解决立体几何截面问题的解题策略．
①坐标法：将几何问题转化为一种代数运算．
②基底法：利用平面向量及空间向量基本定理作为依托，其理论依据是：若四点E、F、G、H共面，P为空间任意点，则有：
③几何法：从几何视角人手，借助立体几何中的线线平行、线面平行、面面平行的性质与判定定理以及平面几何相关定理、结论，通过论证，精准找到该截面与相关线、面的交点位置、依次连接这些点，从而得到过三点的完整截面，再依据题意完成所求解答或证明．
3.数学运算—空间向量在立体几何中的应用
【分析】（1）建立空间直角坐标系， 利用向量坐标相等证明；
[2023年新课标I卷第18题]
等腰三角形性质：“三线合一”，解题的关键
证明异面直线垂直基本方法是：转化为线面垂直
[2023年新课标II卷第20题]
利用勾股定理证明线线垂直不要忽视平面几何知识
【思维导引】现成的两两垂直，能不能建立空间直角坐标系，用向量法证明呢？
【思维导引】利用空间向量法求解线面角
（1）立体几何解答题考查的知识点基本固定
立体几何是高考解答题必考题型之一，第一问一般可通过传统法解决，常考平行和垂直关系，或者体积，表面积问题；第二问一般通过建系解决，常涉及到线面角，二面角的求解，或者已知线面角，面面角求参数，其中法向量是考查的重点。 立体几何解答题的难度已中档题居多，难题偏少，需重点备考，力争得满分。
（2）向量法是解决立体几何解答题的主要方法
（3）难建立空间直角坐标系
（ii）线段长度不明确
点评：三棱柱中已知的线段长度只有侧棱长、点面距、线线距，在建系的过程中我们设了三个未知量， 加大了解题难度。
（4）建立好空间直角坐标系，一定要准确写出点的坐标
常用到的方法： ①射影法（经常用）； ②公式法（中点坐标公式、重心坐标公式等） ③向量法（利用平行、垂直关系求点的坐标；利用三角形法则或平行四边形法则求坐标；利用三点共线设坐标） ④几何法（把空间问题转化为平面问题，常见于利用相似三角形的性质） ⑤待定系数法（设出点的坐标，利用已知条件求出点的坐标）
（5）重视基向量法的应用
教材 选必一，P32 例题4
教材 选必一，P36 例题7
[点评] 距离问题是培养学生直观想象、逻辑推理和数学运算素养的很好的载体，主要解题方法有（1）几何法：找垂足求线段长、等面积法、等体积法；（2）向量法
（6）用向量法求距离问题
（7）重视平面几何知识与解三角形在立体几何中的应用
几何法中多次用到了勾股定理
点评：两次全等、两次余弦定理、三角形面积公式。
如三角形的相似、全等、中位线的性质、勾股定理等性质；特殊三角形：直角三角形、等腰三角形的性质；平行四边形、菱形的性质；④等腰梯形、直角梯形的性质、正六边形性质；⑤圆的性质.
4.逻辑推理—几何法在立体几何中的应用
利用勾股定理证明线线相等
（1）熟练掌握点线面的位置关系；（2）熟练掌握线面垂直、平行的判定定理、性质定理；（3）学会做辅助线找空间角、距离；（4）用规范的符号语言描述解题思路，避免歧义；
几何法对考生思维的灵活性上、严谨性上提出了更高的要求，充分的考查逻辑推理能力。
回归教材，建立完整的知识体系；
夯实基础，提升应对新高考的能力；
研究真题，把握新高考的命题导向；
抓住本质，培养解决问题的核心素养；
1.回归教材，建立完整的知识体系
（1）熟悉教材，抓住知识间的联系
人教A版•选择性必修一
教材是落实数学课程目标、培养学生数学核心素养的重要教学资源，也是历年高考命题的重要素材。所以，教材是高考复习的重要依托。 高三备考阶段，应回归教材进行系统回顾与归纳，要对教材进行再阅读和再理解；特别要重视教材中的重要公式和定理的推导过程，帮助学生建立系统的知识体系。
在梳理数学知识间联系、探寻基本的解题思想和方法的同时，还要重视引导学生关注教材中的例题和习题，以及阅读、探究等栏目（如图），挖掘其中蕴含的思想，拓展相关知识、开阔视野，提炼出通性、通法，准确的把握知识的本质。
（2）教材中见高考真题的“影子”
教材选必一，P10习题1.3,第3题
教材选必一，P43习题1.4,第10题
[2023年新课标I卷第12题]
教材必修二，P154 例6
[2023年新课标I卷第14题]
[2023年新课标II卷第14题]
教材选必一，P10习题1.1，第10题
先证EFGH为平行四边形
【试题亮点】试题以圆锥为背景，问题设计源于教材，重视基础性、综合性的考查，要求考生对圆锥的体积、侧面积以及平面与平面之间的位置关系等基本知识有较全面的理解，试题准确把握数学课程标准，注重数学核心素养，关注学生学习实际，对中学数学教学起到积极的导向作用。
2.研究真题，把握新高考的命题导向
新课程、新教材、新高考背景下，“一核”、“四层”“四翼”的高考评价体系，推动着高考命题的变革，促使高考考查目标由能力立意向素养导向转变。 在复习备考时，教师要认真思考和研究高考数学的命题方向和命题原则。明确考什么、怎样考，弄清各个单元和主题的必备知识、关键能力以及承载的学科素养。同时，要认真研究高考真题，挖掘它在各个知识点上体现的命题导向（左图）
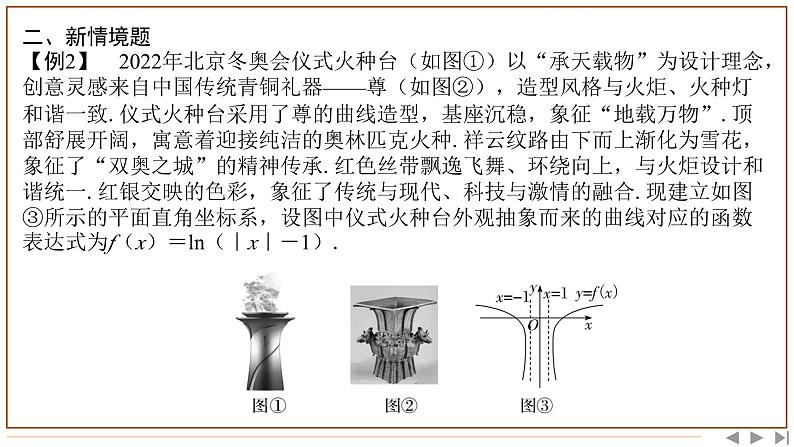
【试题分析】(1)传统建筑安装灯带是一个实际问题，试题巧妙地将此问题抽象成一个五面体棱长的问题，具有很好的创新性。题目中蕴含了数学抽象、数学建模等丰富的数学思想。对考生从数学角度发现问题、提出问题、分析问题、解决问题的能力提出了较高要求。 (2)本题与中国传统建筑文化相结合，真正实现了高考“立德树人、服务选才、引导教学”的核心功能。
【试题分析】 试题以必备知识正四棱锥和球设置探索创新情境。试题的正确运算必须基于空间想象，同时还必须依靠严密的逻辑推理，才能发现空间几何体中相关量之间的关系，进而完成对问题的求解。 试题在考查立体几何基础知识、基本方法的同时，侧重考查考生的构图能力、空间想象能力、逻辑推理能力和运算求解能力等关键能力。
[教材选必一P43，习题]
[教材必修二P165，习题]
【试题分析】动态几何问题，让学生在解题中，完整经历直观感知、动手操作、模式识别、逻辑推理、规范表达的过程，帮助学生建立较强的空间想象能力。
[点评]空间动态问题，是高考常考题型，常以客观题出现．常见题型有空间位置关系判定、轨迹问题、最值问题、范围问题等．
[常用的思路](1)直观判断：在变化过程中判断点、线、面在何位置时，所求的量有相应最大、最小值，即可求解．(2)函数思想：通过建系或引入变量，把这类动态问题转化为目标函数，从而利用代数方法求目标函数的最值如：[2022年新高考I卷8题]．
3.夯实基础，提升应对新高考的能力
（1）理解并记忆空间几何体涉及到的公式，公理，性质定理与判定定理。并熟练掌握每一个公理或定理的作用；
（2）学会画图，能够构建符合题目要求的图形，以便快速找到内在联系。 高考题在这部分的考查基本上2—3个小题，而且大多数没有图形，快速的画出符合题目要求的图形显得尤为重要，这就要求学生不仅要学会画图，而且要对常见的图形具有的性质做到“了如指掌”。
在∆PBC中已知三边容易得到所求三角形的面积
点评：对常见图形的了解，可以大大简化求解过程，小题小做，不必展开。
教材必修二，P138 例3
文字语言、符号语言、图形语言的转化
（3）熟练掌握基本模型（切接模型，正方体模型，长方体模型，在长方体的8个顶点中，任取四个构成的三棱锥模型，外接球模型）
（4）掌握垂直、平行问题处理的一般方法，特别是怎样做辅助线；（5）掌握空间角的基本概念，能利用几何法（定义法）处理简单的空间角问题；（6）掌握利用向量法解决空间几何体问题的一般方法和书写格式；（7）注意解三角形与平面几何知识在解题中的应用。
4.抓住本质，培养解决问题的核心素养
人教A版•必修二P165（教材中的基本图形）
提高数学复习的品位，要从提高思想站位开始。要立足核心素养去培养学生的问题解决能力，要以辩证的观点看待问题，以转化的思想对待问题，以一般性和特殊性去分析问题，始终以空间图形的特征和位置关系作为关键，突出立体几何中“观察、判断、计算、证明”的解题的途径，综合与灵活地应用立体几何的知识、思想方法解决问题。
[点评]鼓励学生灵活选择运用向量方法与几何方法，从不同角度解决立体几何问题，引导多维思考，凸显问题本质，提升学生问题解决的数学核心素养.
从2023年高考立体几何试题的分析不难得出，立体几何考查的主要内容大都以简单、熟悉的空间几何体为载体.这也是数学课程标准中一再提到的借助长方体来研究问题的初心.因此复习过程中，要充分利用简单几何体模型，研究其典型结构特征，深度挖掘蕴含的空间点、直线、平面之间的位置关系，进而梳理立体几何知识体系，形成解决立体几何问题的基本思维模式.复习备考中要关注立体几何文字语言、符号语言及图形语言之间的转化,要注重通用通法，在深刻理解的基础上融会贯通，灵活运用，举一反三，主动进行探究和深层次学习，而不是把精力放在解题的技巧性上.