






- 新教材2023_2024学年高中数学第六章概率本章总结提升课件北师大版选择性必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第七章统计案例1一元线性回归1.1直线拟合1.2一元线性回归方程课件北师大版选择性必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第七章统计案例2成对数据的线性相关性2.1相关系数2.2成对数据的线性相关性分析课件北师大版选择性必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第七章统计案例本章总结提升课件北师大版选择性必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学数学文化课件北师大版选择性必修第一册 课件 0 次下载
数学选择性必修 第一册3.3 独立性检验的应用教课课件ppt
展开基础落实·必备知识全过关
重难探究·能力素养全提升
成果验收·课堂达标检测
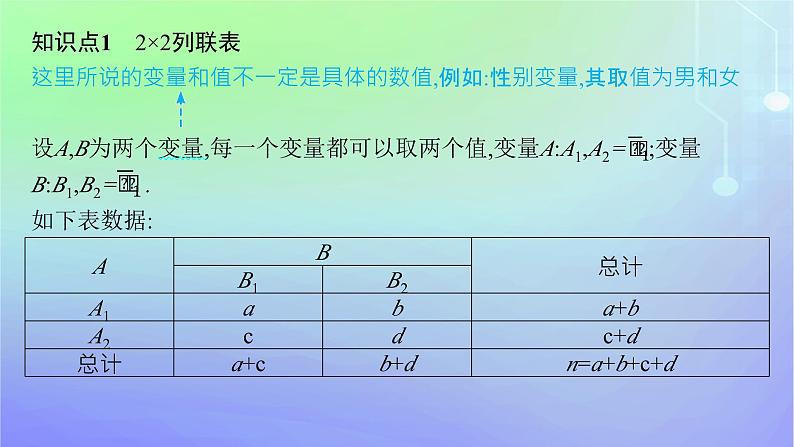
知识点1 2×2列联表这里所说的变量和值不一定是具体的数值,例如:性别变量,其取值为男和女 设A,B为两个变量,每一个变量都可以取两个值,变量A:A1,A2= ;变量B:B1,B2= .如下表数据:
其中,a表示变量A取A1,且变量B取B1时的数据;b表示变量A取A1,且变量B取B2时的数据;c表示变量A取A2,且变量B取B1时的数据;d表示变量A取A2,且变量B取B2时的数据.上述是一张2行2列的表,在统计中称为2×2列联表.名师点睛制作2×2列联表的基本步骤第一步,合理选取两个变量,且每一个变量都可以取两个值;第二步,抽取样本,整理数据;第三步,画出2×2列联表.
过关自诊[人教A版教材习题]根据有关规定,香烟盒上必须印上“吸烟有害健康”的警示语.那么(1)吸烟是否对每位烟民一定会引发健康问题?(2)有人说吸烟不一定引起健康问题,因此可以吸烟.这种说法对吗?
解 (1)从已掌握的知识来看,吸烟会损害身体的健康.但除了吸烟之外,身体的健康还受许多其他随机因素的影响,它是很多因素共同作用的结果.(2)这种说法不正确.虽然吸烟不一定会对每个人都引起健康问题,但根据统计数据,吸烟比不吸烟引起健康问题的可能性大,所以“吸烟不一定引起健康问题,因此可以吸烟”的说法是不对的.
知识点2 独立性检验1. ,用χ2的大小可以对变量A,B的独立性进行判断.2.要推断“变量A与B的关联程度”,可按下面的步骤进行:(1)根据2×2列联表计算 的值; (2)用以下结果对变量的独立性进行判断.①当χ2≤2.706时,没有充分的证据判断变量A,B有关联,可以认为变量A,B是没有关联的;②当χ2>2.706时,有90%的把握判断变量A,B有关联;③当χ2>3.841时,有95%的把握判断变量A,B有关联;④当χ2>6.635时,有99%的把握判断变量A,B有关联.
过关自诊[人教A版教材习题]假设随机抽取了44名学生,按照性别和体育锻炼情况整理为如下的列联表:单位:人
(1)据此推断性别因素是否影响学生锻炼的经常性;(2)说明你的推断结论是否可能犯错,并解释原因.
(2)推断可能犯错误.因为样本是通过随机抽样得到的,频率具有随机性,因此推断可能犯错误.
探究点一 2×2列联表及应用
【例1】 为了解人们对于国家颁布某政策的热度,某市进行调查,随机抽调了55人,他们年龄的频数分布及支持这项政策人数如表所示:
由以上统计数据填下面2×2列联表:
规律方法 准确理解给定信息,找准分类变量,然后将数据依次填入相应空格内.
变式训练1某校高二年级共有1 600名学生,其中男生960名,女生640名,该校组织了一次满分为100分的数学学业水平模拟考试.根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),不到40分的学生只能取得D等(不合格).为研究这次考试成
绩优秀是否与性别有关,现按性别采用分层随机抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]七组加以统计,绘制成如图所示的频率分布直方图.
(1)估计该校高二年级学生在正式的数学学业水平考试中成绩不合格的人数;(2)请你根据已知条件将下列2×2列联表补充完整.
解 (1)设抽取的100名学生中,本次考试成绩不合格的有x人,根据题意得x=100×[1-10×(0.006+0.012×2+0.018+0.024+0.026)]=2.据此估计该校高二年级学生在正式的数学学业水平考试中成绩不合格的人数为 ×1 600=32(人).
(2)根据已知条件得2×2列联表:
探究点二 χ2统计量及计算
【例2】 根据下表计算:
则χ2≈ .(保留3位小数)
规律方法 列联表中的数据信息与χ2统计量之间的关系要对应,其次,需对公式的结构有清醒的认识.
变式训练2已知列联表:药物效果与动物试验列联表
则χ2≈ .(结果保留3位小数)
探究点三 独立性检验基本思想的实际应用
【例3】 调查在2~3级风的海上航行中男女乘客的晕船情况,结果如下表所示:
根据此资料,你是否认为在2~3级风的海上航行中男人比女人更容易晕船?
解 由公式得 .因为0.08<2.706,所以我们没有理由认为男人比女人更容易晕船.
规律方法 独立性检验的基本思想及步骤
变式训练3在某测试中,卷面满分为100分,60分以上为及格,为了调查午休对本次测试前两个月复习效果的影响,特对复习中进行午休和不进行午休的考生进行了测试成绩的统计,数据如下表所示:
(1)根据上述表格完成列联表:
(2)根据列联表可以得出什么样的结论?对今后的复习有什么指导意义?
解 (1)根据题表中数据可以得到列联表如下:
(2)由公式得 ,因为5.73>3.841,所以我们有95%的把握认为午休与考生考试及格有关系,并且午休的及格率高,所以在以后的复习中考生应尽量适当午休,以保持最佳的学习状态.
1.知识清单:(1)2×2列联表.(2)独立性检验的应用.2.核心素养:数据处理.3.常见误区:对χ2的理解,结论的表述不当,不能认识到独立性检验是描述了两个变量相关联的可能性的大小.
1.给出下列实际问题:①一种药物对某种病的治愈率;②两种药物治疗同一种病是否有区别;③吸烟者得肺病的概率;④吸烟人群是否与性别有关系;⑤网吧与青少年的犯罪是否有关系.其中用独立性检验可以解决的问题有( )A.①②③B.②④⑤C.②③④⑤D.①②③④⑤
2.当χ2>3.841时,认为事件A与事件B( )A.有95%的把握有关联B.有99%的把握有关联C.没有理由说它们有关联D.不确定
3.在研究肥胖与高血压的关系时,通过收集数据、整理分析数据得到“高血压与肥胖有关”的结论,并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的,下列说法中正确的是( )A.在100个肥胖的人中至少有99人患有高血压B.肥胖的人至少有99%的概率患有高血压C.在100个高血压患者中一定有肥胖的人D.在100个高血压患者中可能没有肥胖的人
解析 由题知“高血压与肥胖有关”,并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的,表示有99%的把握认为这个结论成立,与多少个人患高血压没有关系,也不是说“肥胖的人就是至少有99%的概率患有高血压”,只有选项D正确.
4.在一项打鼾与患心脏病的调查中,共调查了1 671人,经过计算χ2≈27.63,根据这一数据分析,我们有理由认为打鼾与患心脏病 (填“有关”或“无关”).
5.某大学在研究性别与职称(分正教授、副教授)之间是否有关系,你认为应该收集哪些数据?
女正教授人数、男正教授人数、女副教授人数、男副教授人数
高中北师大版 (2019)3.3 独立性检验的应用作业课件ppt: 这是一份高中北师大版 (2019)3.3 独立性检验的应用作业课件ppt,共17页。
高中3.3 独立性检验的应用教学课件ppt: 这是一份高中3.3 独立性检验的应用教学课件ppt,共14页。PPT课件主要包含了我喜欢听古典音乐,我只听流行音乐,容易生气患上心脏病,每天笑哈哈百病不生,什么是独立性检验,谢谢大家等内容,欢迎下载使用。
高中北师大版 (2019)3.2 独立性检验的基本思想教学课件ppt: 这是一份高中北师大版 (2019)3.2 独立性检验的基本思想教学课件ppt,共15页。PPT课件主要包含了谢谢大家等内容,欢迎下载使用。













