高中数学北师大版 (2019)选择性必修 第一册第七章 统计案例2 成对数据的线性相关性2.2 成对数据的线性相关性精练

第七章§2　成对数据的线性相关性

2.1　相关系数　2.2　成对数据的线性相关性分析

A级 必备知识基础练

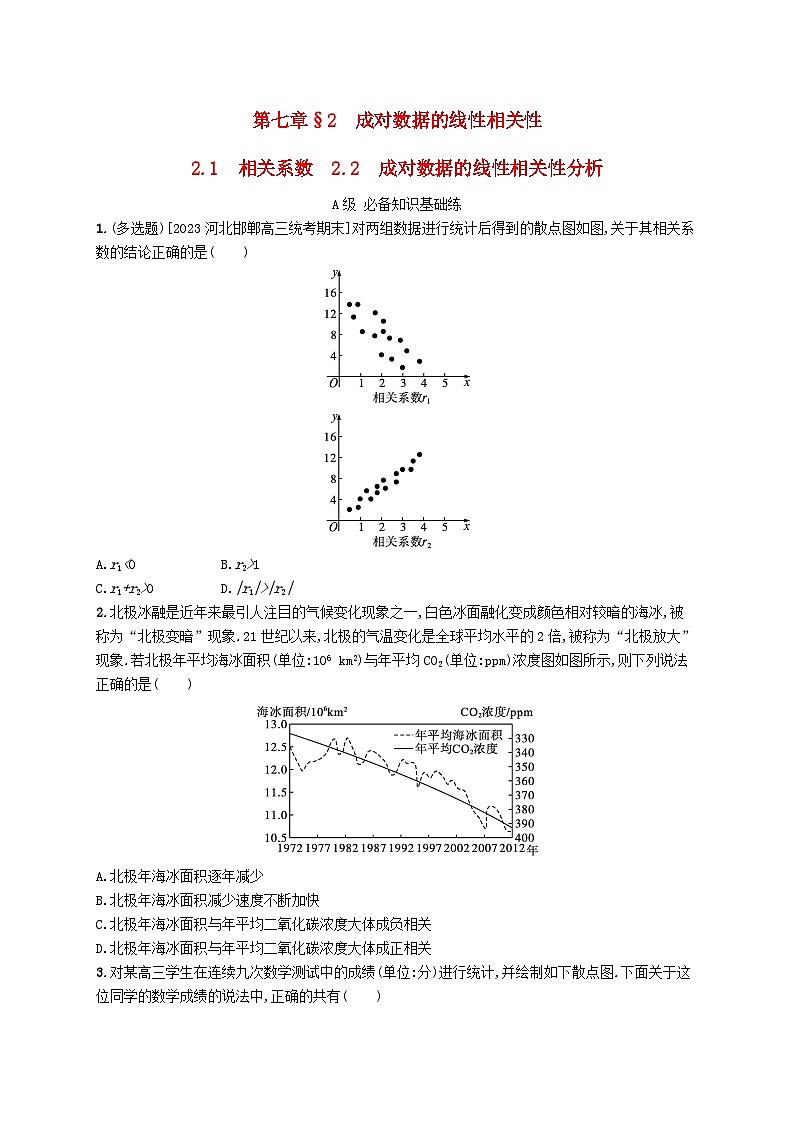
1.(多选题)[2023河北邯郸高三统考期末]对两组数据进行统计后得到的散点图如图,关于其相关系数的结论正确的是(　　)

A.r1<0 B.r2>1

C.r1+r2>0 D.|r1|>|r2|

2.北极冰融是近年来最引人注目的气候变化现象之一,白色冰面融化变成颜色相对较暗的海冰,被称为“北极变暗”现象.21世纪以来,北极的气温变化是全球平均水平的2倍,被称为“北极放大”现象.若北极年平均海冰面积(单位:106 km2)与年平均CO2(单位:ppm)浓度图如图所示,则下列说法正确的是(　　)

A.北极年海冰面积逐年减少

B.北极年海冰面积减少速度不断加快

C.北极年海冰面积与年平均二氧化碳浓度大体成负相关

D.北极年海冰面积与年平均二氧化碳浓度大体成正相关

3.对某高三学生在连续九次数学测试中的成绩(单位:分)进行统计,并绘制如下散点图.下面关于这位同学的数学成绩的说法中,正确的共有(　　)

①该同学的数学成绩总的趋势是在逐步升高;

②该同学在这连续九次测试中的最高分与最低分的差超过40分;

③该同学的数学成绩与考试次数具有线性相关性,且为正相关.

A.0个 B.1个 C.2个 D.3个

4.现随机抽取了某中学高一10名在校学生,他们入学时的数学成绩X与入学后第一次考试的数学成绩Y如下表:

请问:这10名学生的两次数学成绩是否具有线性相关关系?

注:若|r|>0.75,则我们可以认为Y与X之间具有较强的线性相关关系.

5.维尼纶纤维的耐热水性能的好坏可以用指标“缩醛化度” Y来衡量,这个指标越高,耐热水性能也越好,而甲醛浓度是影响缩醛化度的重要因素,在生产中常用甲醛浓度X(单位:g/L)去控制这一指标,为此必须找出它们之间的关系,现安排一批实验,获得如下数据:

(1)画出散点图;

(2)求Y关于X的线性回归方程;

(3)求相关系数r.

B级 关键能力提升练

6.如图,有6组数据,去掉哪组数据后(填字母代号),剩下的5组数据的线性相关性最大(　　)

A.A B.B C.C D.D

7.设(x1,y1),(x2,y2),…,(xn,yn)是变量X和Y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论正确的是(　　)

A.直线l过点()

B.X和Y的相关系数为直线l的斜率

C.X和Y的相关系数在0到1之间

D.当n为偶数时,分布在l两侧的样本点的个数一定相同

8.恩格尔系数是食品支出总额占个人消费支出总额的比重.居民可支配收入是居民可用于最终消费支出和储蓄的总和,即居民可用于自由支配的收入.如图为我国2013年至2019年全国恩格尔系数和居民人均可支配收入的折线图.

恩格尔系数

居民人均可支配收入

下列三个结论:

①恩格尔系数与居民人均可支配收入之间存在负相关关系;

②一个国家的恩格尔系数越小,说明这个国家越富裕;

③一个家庭收入越少,则家庭收入中用来购买食品的支出所占的比重就越小.

其中正确的是(　　)

A.① B.② C.①② D.②③

9.某学校开展研究性学习活动,一组同学获得了下面的一组试验数据:

现有如下5个模拟函数:

①Y=0.58X-0.16;②Y=2X-3.02;③Y=X2-5.5X+8;④Y=log2X;⑤Y=+1.74.

请从中选择一个模拟函数,使它能近似地反映这些数据的规律,应选　　　　.(填序号) 

10.某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:

该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.

(1)求选取的2组数据恰好是不相邻2天数据的概率;

(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出Y关于X的线性回归方程Y=X+;

(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?

11.流行性感冒(简称流感)是流感病毒引起的急性呼吸道感染,是一种传染性强、传播速度快的疾病.它主要通过空气中的飞沫、人与人之间的接触或与被污染物品的接触传播.流感每年在世界各地均有传播,在我国北方通常呈冬春季流行,南方有冬春季和夏季两个流行高峰.某幼儿园将去年春季该园患流感的小朋友按照年龄X与人数Y统计,得到如下数据:

(1)求Y关于X的线性回归方程;

(2)计算样本相关系数r(计算结果精确到0.01),并回答是否可以认为该幼儿园去年春季患流感人数与年龄负相关性很强?(若|r|∈[0.75,1],则X,Y相关性很强;若|r|∈(0.3,0.75),则X,Y相关性一般;若|r|∈[0,0.3],则X,Y相关性较弱.)

参考数据:≈5.477.

参考公式:,

样本相关系数r=.

C级 学科素养创新练

12.[2023四川成都新都一中高二期末]中国有句话叫民以食为天,中国人认为吃对于人来说是一件很重要的事情,不但要能吃,也要会吃.但是好吃不等于健康,有人对不同类型的某些食品做了一次调查,制作了下表.其中X表示某种食品所含热量的百分比,Y表示一些人以百分制给出的对应的评分.

(1)试用r对两个变量X,Y的相关性进行分析(r的结果保留两位小数);

(2)求Y关于X的线性回归方程.

参考公式:r=.

参考数据:≈13.60.

参考答案

§2　成对数据的线性相关性

2.1　相关系数

2.2　成对数据的线性相关性分析

1.AC　由散点图可知,相关系数r1的图象表示y与x负相关,故-1<r1<0,故A正确;相关系数r2的图象表示y与x正相关,故0<r2<1,故B错误;因为相关系数r2的点较相关系数r1的点密集,故|r2|>|r1|,故r1+r2>0,故C正确,D错误.

2.C　

3.D

4.解 由表计算得,=107.8,

=68,

=116584,

=47384,

xiyi=73796.

所以样本相关系数为

r=

=

=

≈0.7506>0.75.

由此可看出这10名学生的两次数学成绩线性相关.

5.解 (1)散点图如图.

(2)可以看出,两变量之间有近似的线性相关关系,下面用列表的方法计算

=24,,

0.264 3,

22.648,

∴线性回归方程为Y=22.648+0.264 3X.

(3)5 892,

r=

=

≈0.96.

6.C　7.A

8.C　由折线图可知,恩格尔系数在逐年下降,居民人均可支配收入在逐年增加,故两者之间存在负相关关系,恩格尔系数越小,居民人均可支配收入越多,经济越富裕,故结论①②正确.一个家庭收入越少,则家庭收入中用来购买食品的支出所占的比重越大,故③错误.

9.④

10.解 (1)设事件A表示“选取的2组数据恰好是不相邻2天的数据”,则表示“选取的数据恰好是相邻2天的数据”.

样本点总数为10,事件包含的样本点数为4.

∴P()=,

∴P(A)=1-P()=

(2)=12,=27,xiyi=977,=434,

=2.5,

=27-2.5×12=-3,

∴Y=2.5X-3.

(3)由(2)知:当X=10时,Y=22,误差不超过2颗;

当X=8时,Y=17,误差不超过2颗.

故所求得的线性回归方程是可靠的.

11.解 (1)由题意可得=4,

=17,

=-3.2,

=17+3.2×4=29.8.

故Y关于X的线性回归方程为Y=-3.2X+29.8.

(2)r=-0.97,

由r<0,可知X,Y负相关.又因为|r|接近于1,所以X,Y相关性很强.因此,可以认为该幼儿园去年春季患流感人数与年龄负相关性很强.

12.解 (1)易得=25,

=80,

(xi-)2=(-10)2+(-5)2+02+52+102=250,

(yi-)2=(-12)2+(-2)2+02+22+122=296,

(xi-)(yi-)=-10×(-12)+(-5)×(-2)+0+5×2+10×12=260,

所以r=0.96,

0.96∈[0.75,1],即r为正且接近于1,

所以两个变量X,Y之间正相关,并且有较强的相关性.

(2)由(1)易得=1.04,

=80-1.04×25=54,

所以Y关于X的线性回归方程为Y=1.04X+54.