精品解析：广东省深圳市西乡中学2022-2023学年八年级上学期期中考试数学试卷

深圳市西乡中学2022-2023学年第一学期初二年级

数学学科阶段巩固练习

一、选择题

1. 4的平方根是（   ）

A. 4 B.  C.  D. 2

【答案】C

【解析】

【分析】根据平方根的性质，正数有两个平方根且互为相反数，开方求解即可．

【详解】∵一个正数有两个平方根且互为相反数

∴4的平方根是

故选：C．

【点睛】本题主要考查平方根的性质，熟知一个正数有两个平方根并互为相反数是解题的关键，区分平方根与算术平方根是易错点．

2. 下列各数中，是无理数的是（    ）

A. 3.5 B.  C.  D.

【答案】C

【解析】

【分析】根据无理数的定义（无理数是指无限不循环小数）逐个判断即可．

【详解】A、3.5是小数，即分数，属于有理数；

B、是分数，属于有理数；

C、﹣是无理数；

D、＝2，是整数，属于有理数；

故选C．

【点睛】本题考查了无理数的定义，能理解无理数的定义的内容是解此题的关键，注意：无理数有：①开方开不尽的根式，②含π的，③无限不循环小数．

3. 以下列各组数为边长，能构成直角三角形的是（    ）

A. 5，12，13 B. 4，5，6

C. ，， D. 1，1，2

【答案】A

【解析】

【分析】构成直角三角形的三边满足两边的平方和等于第三边，由此即可求解．

【详解】解：选项，，，，则，符合题意；

选项，，，，则，不符合题意；

选项，，，，则，不符合题意；

选项，，，，则，不符合题意；

故选：．

【点睛】本题主要考查运用勾股定理判定直角三角形，理解勾股定理的逆定理是解题的关键．

4. 下列各式，运算正确的是（    ）

A.  B.  C.  D.

【答案】A

【解析】

【分析】直接利用二次根式的性质分别化简计算得出答案．

【详解】解：A、，正确，故此选项符合题意；

B、，原计算错误，故此选项不符合题意；

C、，原计算错误，故此选项不符合题意；

D、=2，原计算错误，故此选项不符合题意．

故选：A．

【点睛】此题主要考查了二次根式的加减运算，正确掌握二次根式加减运算法则是解题关键．

5. 新冠疫情防控形势下，学校要求学生每日测量体温．某同学连续一周的体温情况如表所示，则该同学这一周的体温数据的众数和中位数分别是（　　）

A. 36.3和36.2 B. 36.2和36.3 C. 36.3和36.3 D. 36.2和36.1

【答案】C

【解析】

【分析】根据中位数、众数的意义求解即可．

【详解】解：把已知数据按照由小到大的顺序重新排序后为36.2，36.2，36.3，36.3，36.3，36.4，36.7，

该名同学这一周体温出现次数最多的是36.3℃，共出现3次，因此众数是36.3，

将这七天的体温从小到大排列处在中间位置的一个数是36.3℃，因此中位数是36.3，

故选：C．

【点睛】本题考查中位数、众数，理解中位数、众数的意义是解题的关键．

6. 一次函数的图象经过点，则下列说法不正确的是（    ）

A. y随x的增大而减小 B. 一定经过点

C. 图象不会经过原点 D. 图象不过第三象限

【答案】B

【解析】

【分析】先把点代入一次函数求出解析式，然后再根据一次函数的图象和性质逐一判断即可．

【详解】解：把点代入一次函数，

得，解得，

∴一次函数的解析式为，

且y随x的增大而减小，故A正确，不符合题意，

当时，，

∴图象不经过点，故B不正确，符合题意，

当时，，图象不经过原点，故C正确，不符合题意，

∵，，

∴图象经过第一、二、四象限，故D正确，不符合题意，

故选：B．

【点睛】本题考查了一次函数的图象和性质，熟练掌握一次函数的图象和性质是解题的关键．

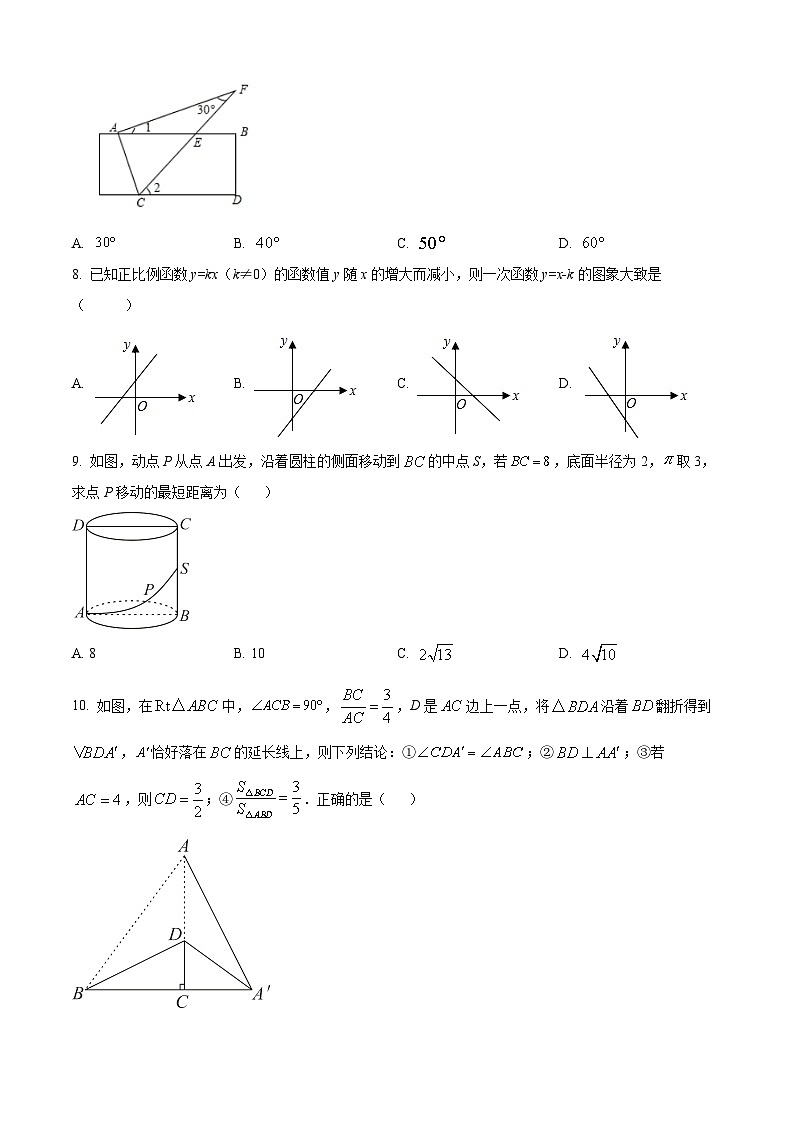
7. 如图将直尺与含30°角的三角尺摆放在一起，若，则的度数是（    ）

A.  B.  C.  D.

【答案】C

【解析】

【分析】先根据三角形外角的性质求出∠BEF的度数，再根据平行线的性质得到∠2的度数．

【详解】如图，

∵∠BEF是△AEF的外角，∠1=20，∠F=30，
∴∠BEF=∠1+∠F=50，
∵AB∥CD，
∴∠2=∠BEF=50，
故选：C．

【点睛】本题主要考查了平行线的性质，解题的关键是掌握三角形外角的性质．

8. 已知正比例函数y=kx（k≠0）的函数值y随x的增大而减小，则一次函数y=x-k的图象大致是（       ）

A.  B.  C.  D.

【答案】A

【解析】

【分析】先根据正比例函数y=kx的函数值y随x的增大而减小，判断出k的符号，再根据一次函数的性质即可得答案．

【详解】解：∵正比例函数y＝kx(k≠0)的函数值y随x的增大而减小，

y＝x-k的图象经过一、二、三象限，

故选A．

【点睛】本题考查的是一次函数的图象与系数的关系，即一次函数y=kx+b (k≠0) 中，当，时，图象经过一、二、三象限．

9. 如图，动点P从点A出发，沿着圆柱的侧面移动到的中点S，若，底面半径为2，取3，求点P移动的最短距离为（    ）

A. 8 B. 10 C.  D.

【答案】C

【解析】

【分析】根据圆柱的侧面展开图，利用勾股定理求出点P移动的最短距离的长度即可．

【详解】解：圆柱的侧面展开图如图，点P移动的最短距离为的长度，

∵，的中点S，

∴，

在中，，，，

∴，

即点P移动最短距离为，

故选：C．

【点睛】本题考查圆柱的侧面展开图、最短路径问题、勾股定理，熟练掌握圆柱的侧面展开图，得出点P移动的最短距离是的长度是解答的关键．

10. 如图，在中，，，D是边上一点，将沿着翻折得到，恰好落在的延长线上，则下列结论：①；②；③若，则；④．正确的是（    ）

A. ①②③ B. ①②④ C. ②③④ D. ①②③④

【答案】D

【解析】

【分析】先通过折叠得出关键的条件，，，，在根据三角形内角和定理判断①；通过条件得出是等腰三角形，再通过三线合一性质判断②；由，，求出，，再根据勾股定理求出判断③；根据前面的计算求出的值，然后再根据同高的三角形面积比等于底边之比求出比值判断④；即可解答．

【详解】解：∵是将沿着翻折得到的，

∴，，，，

∵，

，

∴，故①正确，

延长交于点E，

∵，

∴是等腰三角形，

又∵，

∴既是的角平分线也是的高（三线合一性质），

∴，故②正确，

∵，

若，则，

在中，，

∴，

∴，

∴，

在中，，

即，

解得：，故③正确，

由前面的计算可知，，

∵，，

∴，故④正确，

∴①②③④都正确，

故选：D．

【点睛】本题考查了图形的折叠、等腰三角形、三角形内角和、勾股定理等知识点， 熟练运用折叠的性质得出相应的条件是解题的关键．

二、填空题

11. 点到y轴的距离为___________．

【答案】4

【解析】

【分析】根据点到y轴的距离等于该点横坐标的绝对值求解即可，

【详解】解：∵，

∴点到y轴的距离为4，

故答案为：4．

【点睛】本题考查点到坐标轴的距离，熟练掌握点到x轴距离等于纵坐标的绝对值，点到y轴距离等于横坐标的绝对值是解题的关键．

12. 如图，在中，在数轴上，以B点为圆心，长为半径画弧，交数轴于点D，则D点表示的数是______．

【答案】

【解析】

【分析】根据题意运用勾股定理求出AB的长，即可得到答案．

【详解】解：在△ABC中，∠ACB=90°，BC=2，AC=1，
∴AB=，
∴BD=AB=，
∵B点表示的数是3，
∴点D表示的数为3-．
故答案为：3-．

【点睛】本题考查的是勾股定理，实数与数轴的关系，正确运用勾股定理求出AB的长是解题的关键，要理解数轴上的点与实数的对应关系．

13. 已知函数是关于的一次函数，则的值是_______．

【答案】

【解析】

【分析】函数是一次函数，则，，由此即可求解．

【详解】解：根据题意得，，，

∴，，

∴，

故答案是：．

【点睛】本题主要考查一次函数的定义，理解一次函数的定义，系数不为零，未知数的次数为是解题的关键．

14. 如图，在中，，，是的垂直平分线，且则_____．

【答案】

【解析】

【分析】是的垂直平分线，可知，，设，则，在中根据勾股定理即可求解．

【详解】解：根据题意得，是的垂直平分线，

，

∴,

∴设，

∵，

∴，

∵，，

∴在中，，即，解方程得，，

故答案是：．

【点睛】本题主要考查勾股定理，根据条件确定直角三角形，利用勾股定理是解题的关键．

15. 如图，在四边形中，，连接，若，则______．

【答案】

【解析】

【分析】先过点D作于点E，求出，，然后根据“”证，得出，，最后再根据勾股定理计算即可．

【详解】解：过点D作于点E，

∵，，

∴，

∴，，

∴，

在和中，

，

∴，

∴，，

在中，，

∴，

∴，

在中，，

∴，

在中，，

故答案为：．

【点睛】本题考查了全等三角形和勾股定理的综合，正确构建辅助线证出是解题的关键．

三、解答题

16. 计算：

（1）；

（2）．

【答案】（1）   

（2）

【解析】

【分析】（1）根据二次根式的乘除法法则计算二次根式，再合并二次根式，由此即可求解；

（2）根据平方差公式，完全平方公式展开，在合并二次根式，即可求解．

【小问1详解】

解：

．

【小问2详解】

解：

．

【点睛】本题主要考查二次根式的混合运算及乘法公式的应用，理解和掌握二次根式的加减乘除法法则及乘法公式是解题的关键．

17. 某中学800名学生参加植树节活动，要求每人植3至6棵，活动结束后随机抽查了若干名学生每人的植树量，并分为四种类型，A：3棵；B：4棵；C：5棵；D：6棵，将各类的人数绘制成扇形图（如图1）和条形图（如图2）．

回答下列问题：

（1）这次调查一共抽查了_________名学生的植树量；请将条形图补充完整；

（2）被调查学生每人植树量的众数是________棵，中位数是______棵；

（3）800名学生中，估计有多少名学生种植5棵树？

【答案】（1）20，图见解析   

（2）4，4    （3）240

【解析】

【分析】（1）用B组人数除以B组人数所占的百分比即可求出被抽查的学生人数，用被抽查的学生人数减去A组，B组，C组的学生人数求得D组的学生人数，再补充条形统计图即可．

（2）根据众数的定义和中位数的定义求解即可．

（3）用800乘以被调查人数中植树5棵的人数占的百分比即可．

【小问1详解】

解：名．

故答案为：20．

D组人数为：（名）．

作图如下：

【小问2详解】

解：根据条形统计图可知植树量为4棵的人数为8人，是最多的．

故众数为：4．

将20名学生的植树量从大到小排序后，第10位和第11位分别是4棵和4棵．

故中位数为．

故答案为：4,4；．

【小问3详解】

解：（名）．

答：800名学生中，估计有240名学生种植5棵树．

【点睛】本题考查条形统计图和扇形统计图信息关联，画条形统计图，求众数，求中位数，用样本估计总体，熟练掌握这些知识点是解题关键．

18. 如图，在平面直角坐标系中，三个顶点的坐标分别为．

（1）在图中画出关于y轴的对称图形，并写出；

（2）的面积为________；

（3）若点P在y轴上，则的最小为__________．

【答案】（1）图见解析，-5,3   

（2）9    （3）

【解析】

【分析】（1）利用轴对称性质分别作出A，B，C的关于y轴的对称点，，,顺次连接即可得到所求作图形．

（2）利用长方形的面积减三个直角三角形的面积即可．

（3）利用轴对称的性质，把问题转化为两点之间线段最短解决．

【小问1详解】

解：如图，即为所求，的坐标是，

的坐标是，

故答案为：，

【小问2详解】

的面积 ．

故答案为：9．

【小问3详解】

点C关于y轴的对称点，连接交y轴于点P，连接，此时的值最小，最小值．

故答案为：．

【点睛】本题考查轴对称、轴对称最短问题等知识，解题的关键是学会利用轴对称把最短问题转化为两点之间线段最短．

19. 如图，分别与交于点G、H，．若，，求的度数．

【答案】

【解析】

【分析】由，，得到，由得到，再证得，得到答案．

【详解】证明：∵，，

∴，

∵，

∴，

∴，

∵，

∴，

∴，

∴．

【点睛】本题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解题的关键．

20. 我国是世界上严重缺水的国家之一，为了增强居民的节水意识，某市自来水公司对居民用水采用以户为单位分段计费的办法收费，即一个月用水10吨以内(包括10吨)的用户，每吨收水费a元；一个月用水超过10吨的用户，10吨水仍按每吨a元收费，超过10吨的部分，按每吨b元收费．设一户居民月用水x吨，应交水费y元，y与之间的函数关系如图所示．

（1）填空：______；若某户居民上月用水8吨，应交水费_______元；

（2）求出当时，y与x之间的函数表达式；

（3）若某户居民八月份应缴水费29元，则该户居民八月份用水量是多少？

【答案】（1），应交水费元；   

（2），   

（3）吨

【解析】

【分析】(1)先根据图像求出a的值，进而即可求解；

(2)根据题意当时，可得，然后利用待定系数法求解即可；

(3)把代入，即可得出答案．

【小问1详解】

解：由图像知用水量10吨时应缴水费元，

所以，

，

答：a的值为，某户居民上月用水8吨，应交水费元；

【小问2详解】

解：设，解得，

当时，与之间的函数表达式为，

即；

【小问3详解】

解：因为，所以，

所以，解得，

答：该户居民八月份用水量是17吨．

【点睛】本题考查从图像上获取信息，以及一次函数的应用，根据题意得到一次函数解析式是解题的关键．

21. 如图1，在等腰中，，D是上一点，以为直角边作等腰，连接．

（1）求证：；

（2）若，

①求的长；

②如图2，若F是上一点，，求的长．

【答案】（1）证明见解析   

（2）①；②

【解析】

【分析】（1）根据“”证明出,即可得到；

（2）①通过全等三角形的性质和等腰三角形的性质求出，，再证明是直角三角形，最后根据勾股定理求出 即可；②连接，根据等腰三角形的性质得出，根据三线合一得到，进而得出，从而证明，最后再根据勾股定理求出的长即可解答．

【小问1详解】

证明：由题意可知，，

∴，，

∴，

在和中，

，

∴，

∴；

【小问2详解】

解：①由（1）可知，

∴，，

∵等腰直角三角形，，

∴，，

∴，，

∴，

在中，；

②连接，

∵是等腰直角三角形，，，

又∵，

∴，

∴，

∴是等腰的角平分线，

∴是等腰的高和底边的平分线（三线合一性质），

∴，，

∴，

在和中，

，

∴，

∴，

∴，

在中，，

即，

解得：，

∴．

【点睛】本题考查了全等三角形的判定和性质，等腰直角三角形的性质，三线合一性质，勾股定理等知识点，属于综合性比较强的题型，熟练运用相关知识是解题的关键．

22. 如图1，直线的解析式为，点坐标为，点关于直线的对称点点在直线上．

（1）点的坐标为________；

（2）如图1，在轴上是否存在点，使与的面积相等，若存在，求出点坐标，若不存在，请说明理由；

（3）如图2，已知过点的直线，与直线夹角恰好等于，请直接写出直线的表达式．

【答案】（1）   

（2）存在，或，理由见详解   

（3）或

【解析】

【分析】（1）直线的解析式为，可知直线与轴交点的坐标为，点坐标为，在中，可求出的长度，点关于直线的对称点点在直线上，则有，，由此即可求解；

（2）根据（1）中信息，可知的面积为，设点，则，所以，由此即可求解；

（3）如图所示（见详解），过作与，设，在，，，中，可求出，，，，值，且有，由此即可求解．

【小问1详解】

解：根据题意得，，，

∴在中，，

由对称性质得：，，，

设点，则，

∴，，

在中，，即，解方程得，，

∴点的坐标是．

【小问2详解】

解：存在，理由如下，

已知，，，

∴直线的解析式是，直线的解析式是，如图所示，

设点，则，，

∴，解方程得，或，

∴点或．

【小问3详解】

解：如图所示，与轴交于点，过作与，

由（1）可知，，，设，

∴在中，，

在中，，

在中，，

∴，

∴，，

在中，，即，

解方程得，，，

∴或

当，时，的直线方程是；

当，时，的直线方程是．

综上所述，过点的直线，与直线夹角恰好等于时，的直线方程是或．

【点睛】本题主要考查了一次函数图像与性质、对称性质、坐标与图形、勾股定理、等腰直角三角形的性质、解方程等知识，掌握一次函数图像的性质，以及图像的变换时点坐标的特点是解题的关键．