精品解析：广东省深圳市光明区公明中学2022-2023学年八年级上学期期中考试数学试卷

光明区公明中学2022-2023学年第一学期八年级期中考试数学试卷

一、选择题（每题3分，共30分）

1. 实数25的算术平方根是（   ）

A. ±5 B. 5 C.  D. ±

【答案】B

【解析】

【分析】根据算术平方根的定义：如果一个正数x的平方等于a，那么这个正数x叫做a的算术平方根，求解即可．

【详解】解：∵（±5）2＝25，
∴25的算术平方根是5．
故选：B．

【点睛】本题主要考查的是算术平方根的定义，掌握算术平方根的定义是解题的关键．

2. 下列根式中，最简二次根式的是（　　）

A.  B.  C.  D.

【答案】C

【解析】

【分析】根据最简二次根式的定义进行求解即可：被开方数不含能开的尽的因数或因式；被开方数的因数是整数，因式是整式

【详解】解：A、，不是最简二次根式，不符合题意；

B、，不是最简二次根式，不符合题意；

C、是最简二次根式，符合题意；

D、，不是最简二次根式，不符合题意；

故选C．

【点睛】本题主要考查了最简二次根式，熟知最简二次根式的定义是解题的关键．

3. 无理数的估算值为（　　）

A.  B.  C.  D.

【答案】C

【解析】

【分析】用“夹逼法”估算即可．

【详解】解： ，

，

故选：C．

【点睛】此题考查了估算无理数的大小，解题的关键是掌握首先估算被开方数在哪两个相邻的平方数之间，再估算该无理数在哪两个相邻的整数之间．

4. 在下列长度的各组线段中，能组成直角三角形的是(    )

A. 5，6，7 B. 5，12，13 C. 1，4，9 D. 5，11，12

【答案】B

【解析】

【详解】解：A、∵52+62≠72，故不能围成直角三角形，此选项错误；

C、∵12+42≠92，故不能围成直角三角形，此选项错误；

B、∵52+122=132，能围成直角三角形，此选项正确；

D、∵52+112≠122，故不能围成直角三角形，此选项错误．

故选：B．

【点睛】本题考查了勾股定理的逆定理，熟知勾股数是解决本题的关键.

5. 已知M，a>0，且ab＜0，那么点M在（　　）

A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

【答案】D

【解析】

【分析】点所在的象限与点的横纵坐标的符号有关，由已知条件，判断出的符号，进而得出结论．

【详解】∵a>0，ab＜0，

∴b＜0，∴a、b异号，

∴点（a，b）在第四象限．

故选：D．

【点睛】本题是判断点的坐标所在象限的题目，需要利用各象限内点的坐标特征进行解答．

6. 若一个直角三角形的三边长分别为3，4，x，则x的值是（    ）

A. 4 B. 5 C. 7 D. 5或

【答案】D

【解析】

【详解】试题解析：设第三边为x
（1）若4是直角边，则第三边x是斜边，由勾股定理，得
32+42=x2，所以x=5
（2）若4是斜边，则第三边x为直角边，由勾股定理，得
32+x2=42，所以x=．
所以第三边的长为5或．
故选D．

点睛：已知直角三角形的两边长，但未明确这两条边是直角边还是斜边，因此两条边中的较长边4，既可以是直角边，也可以是斜边，所以求第三边的长必须分类讨论，即4是斜边或直角边的两种情况，然后利用勾股定理求解．

7. 点P关于y轴的对称点的坐标为（　　）

A.  B.  C.  D.

【答案】C

【解析】

【分析】利用关于轴对称点坐标特点：横坐标互为相反数，纵坐标不变，即点关于轴的对称点的坐标为，进而得出答案．

【详解】解：点关于y轴对称的点的坐标为，

故选：C．

【点睛】本题主要考查了关于轴对称点的性质，正确把握对称点的横、纵坐标的关系是解题的关键．

8. 下列函数中，是一次函数的是（　　）

A.  B.  C.   D.

【答案】D

【解析】

【分析】根据一次函数的定义，对选项逐个判断即可，形如（）的函数为一次函数．

【详解】解：A、该函数不是一次函数，故本选项错误，不符合题意；

B、该函数不是一次函数，故本选项错误，不符合题意；

C、该函数不是一次函数，故本选项错误，不符合题意；

D、该函数符合一次函数的定义，故本选项正确，符合题意；

故选：D．

【点睛】此题考查了一次函数的定义，解题的关键是掌握一次函数的定义．

9. 点和在同一直线上，且，，则（　　）

A.  B.  C.  D. 无法确定

【答案】A

【解析】

【分析】根据可得y将随x的增大而减小，利用x的大小关系和函数的增减性可判断．

【详解】解：∵一次函数上，，

∴y随x的增大而减小．

∵，

∴．

故选：A．

【点睛】本题考查一次函数的图象和性质：当，y随x增大而增大；当时，y将随x的增大而减小．

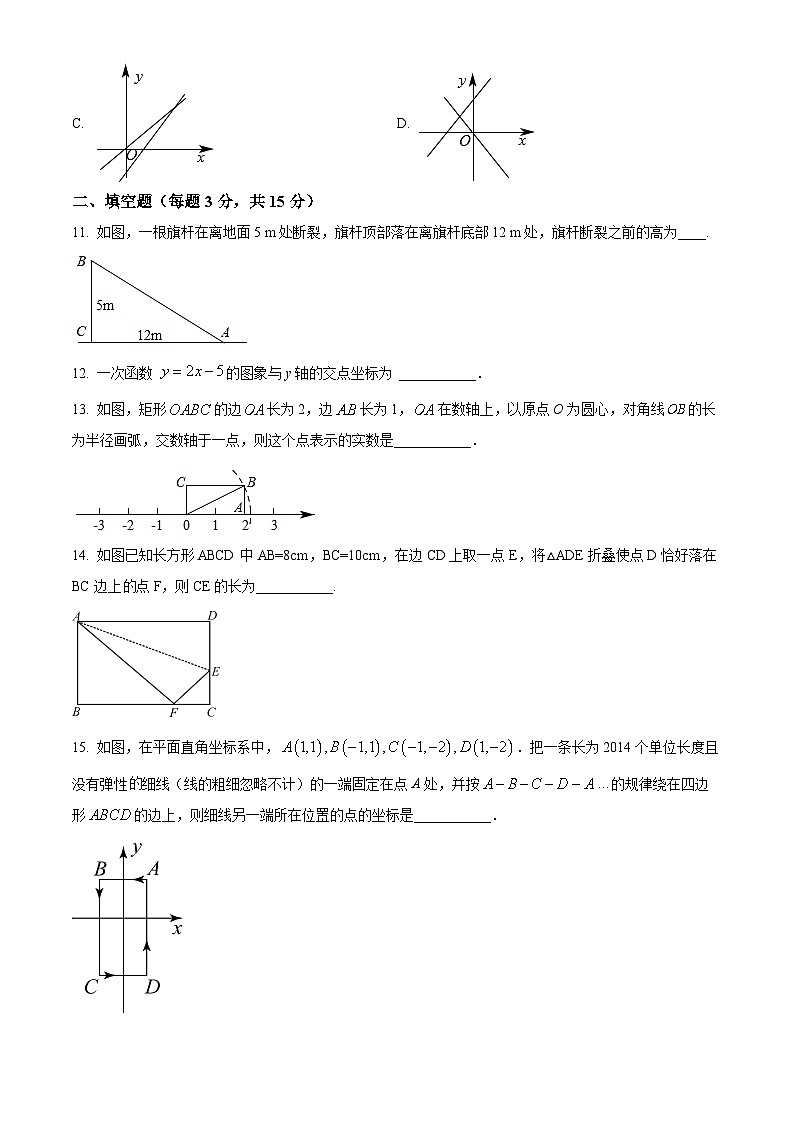
10. 一次函数y＝kx+b与y＝kbx，它们在同一坐标系内的图象可能为（　　）

A.  B.

C.  D.

【答案】A

【解析】

【分析】根据一次函数的图象与系数的关系，有由一次函数y=kx+b图象分析可得k、b的符号，进而可得k•b的符号，从而判断y=kbx的图象是否正确，进而比较可得答案．

【详解】解：根据一次函数的图象分析可得：

A、由一次函数y=kx+b图象可知k＜0，b＞0；一次函数y=kbx的图象可知kb＜0，两函数解析式均成立；

B、由一次函数y=kx+b图象可知k＜0，b＞0；即kb＜0，与次函数y=kbx的图象可知kb＞0矛盾；

C、由一次函数y=kx+b图象可知k＞0，b＜0；即kb＜0，与次函数y=kbx的图象可知kb＞0矛盾；

D、由一次函数y=kx+b图象可知k＞0，b＞0；即kb＞0，与次函数y=kbx的图象可知kb＜0矛盾．

故选：A．

【点睛】本题主要考查了一次函数图象，注意：一次函数y=kx+b的图象有四种情况：

①当k＞0，b＞0，函数y=kx+b的图象经过第一、二、三象限；

②当k＞0，b＜0，函数y=kx+b的图象经过第一、三、四象限；

③当k＜0，b＞0时，函数y=kx+b的图象经过第一、二、四象限；

④当k＜0，b＜0时，函数y=kx+b的图象经过第二、三、四象限．

二、填空题（每题3分，共15分）

11. 如图，一根旗杆在离地面5 m处断裂，旗杆顶部落在离旗杆底部12 m处，旗杆断裂之前的高为____.

【答案】18m

【解析】

【分析】根据勾股定理两个直角边的平方和等于斜边的平方．此题要求斜边和直角边的长度，解直角三角形即可．

【详解】解：旗杆折断后，落地点与旗杆底部的距离为，旗杆离地面折断，且旗杆与地面是垂直的，

所以折断的旗杆与地面形成了一个直角三角形．

根据勾股定理，折断的旗杆为，

所以旗杆折断之前高度为．

故答案为：．

【点睛】本题考查的是勾股定理的正确应用，找出可以运用勾股定理的直角三角形是关键．

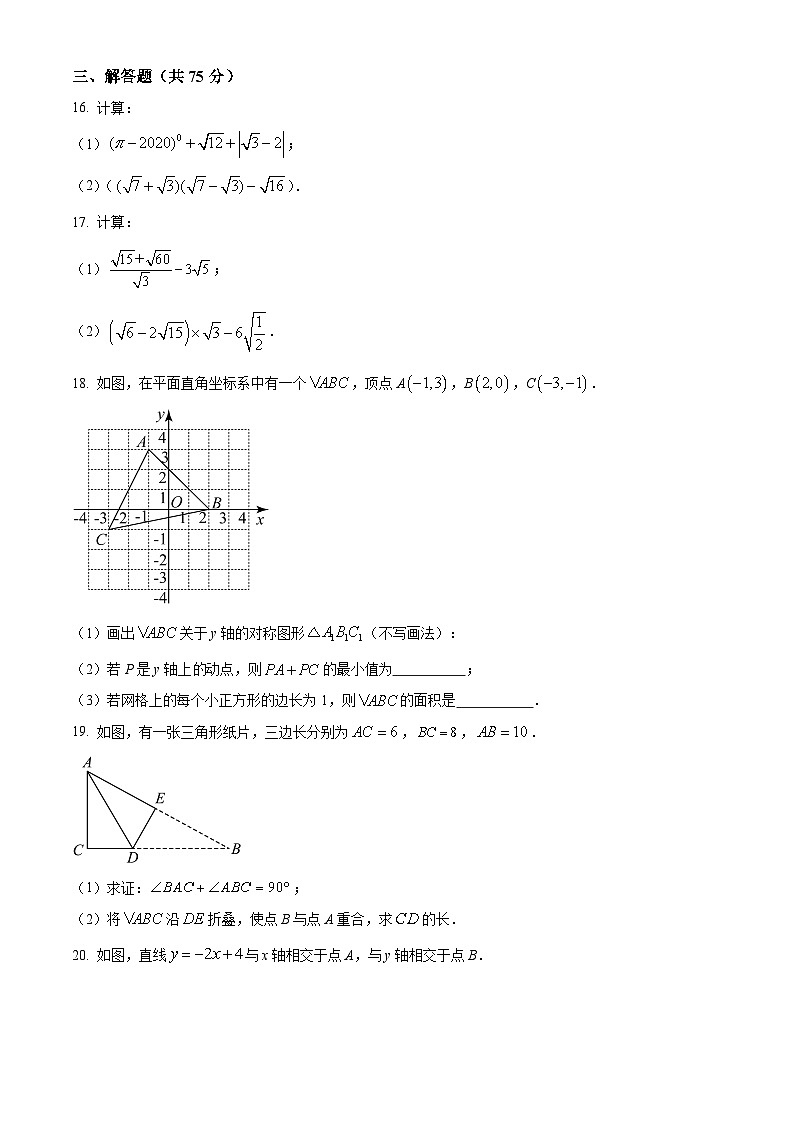
12. 一次函数 的图象与y轴的交点坐标为 ___________．

【答案】

【解析】

分析】令，代入一次函数解析式求出代入一次函数解析式求出y值即可．

【详解】解：当时，，

∴一次函数的图象与y轴的交点坐标是．

故答案为：．

【点睛】本题考查一次函数与坐标轴的交点，熟练掌握y轴上点的坐标特征：横坐标为0是解题的关键．

13. 如图，矩形的边长为2，边长为1，在数轴上，以原点O为圆心，对角线的长为半径画弧，交数轴于一点，则这个点表示的实数是___________．

【答案】

【解析】

【分析】由矩形的边长为2，边长为1，，根据勾股定理求出矩形对角线的长度．以对角线长度为半径作圆与数轴相交，根据交点的位置即可求解．

【详解】解：由勾股定理，得

．

B在原点的右侧时，B点表示的数为，

B在原点的左侧是，B点表示的数为，

故答案为：．

【点睛】本题考查了矩形、勾股定理、实数与数轴的关系，利用勾股定理求出的长是解题关键．

14. 如图已知长方形ABCD中AB=8cm，BC=10cm，在边CD上取一点E，将△ADE折叠使点D恰好落在BC边上的点F，则CE的长为___________.

【答案】3cm

【解析】

【分析】要求CE的长，应先设CE的长为x，由将△ADE折叠使点D恰好落在BC边上的点F可得Rt△ADE≌Rt△AFE，所以AF=10cm，EF=DE=8-x；在Rt△ABF中由勾股定理得：AB2+BF2=AF2，已知AB、AF的长可求出BF的长，又CF=BC-BF=10-BF，在Rt△ECF中由勾股定理可得：EF2=CE2+CF2，即：（8-x）2=x2+（10-BF）2，将求出的BF的值代入该方程求出x的值，即求出了CE的长．

【详解】∵四边形ABCD是矩形，
∴AD=BC=10cm，CD=AB=8cm，
根据题意得：Rt△ADE≌Rt△AFE，
∴∠AFE=90°，AF=10cm，EF=DE，
设CE=xcm,则DE=EF=CD−CE=(8−x)cm，
在Rt△ABF中由勾股定理得：AB2+BF2=AF2，
即82+BF2=102，
∴BF=6cm，
∴CF=BC−BF=10−6=4(cm)，
在Rt△ECF中,由勾股定理可得：EF2=CE2+CF2，
即(8−x)2=x2+42，
∴64−16x+x2=x2+16，
∴x=3(cm)，
即CE=3cm.
故答案为3cm.

【点睛】本题考查翻折变换（折叠问题），解题的关键是掌握折叠的性质和勾股定理.

15. 如图，在平面直角坐标系中，．把一条长为2014个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按…的规律绕在四边形的边上，则细线另一端所在位置的点的坐标是___________．

【答案】

【解析】

【分析】根据题意可得绕四边形一周的细线长度为，再由，可得细线另一端在绕四边形第202圈的第4个单位长度的位置，即可求解．

【详解】解：∵，

∴，

∴绕四边形一周的细线长度为，

∵，

∴细线另一端在绕四边形第202圈的第4个单位长度的位置，

即从点B 向下沿移动2个单位所在的点的坐标即为所求，也就是点．

故答案为：．

【点睛】本题主要考查了点的坐标规律探求，根据点的坐标求出四边形一周的长度，从而确定2014个单位长度的细线的另一端落在第几圈第几个单位长度的位置是解题的关键．

三、解答题（共75分）

16. 计算：

（1）；

（2）（）．

【答案】（1）   

（2）0

【解析】

【分析】（1）根据零指数幂、二次根式的加减运算计算即可；

（2）运用平方差公式、二次根式的混合运算计算即可．

【小问1详解】

原式=；

【小问2详解】

原式=．

【点睛】本题考查实数的混合运算，二次根式的混合运算，零指数幂，正确计算是解题的关键．

17. 计算：

（1）；

（2）．

【答案】（1）0    （2）

【解析】

【分析】（1）根据二次根式混合运算法则进行计算即可；

（2）根据二次根式混合运算法则和二次根式性质进行计算即可．

【小问1详解】

解：

【小问2详解】

解：

【点睛】本题主要考查了二次根式混合运算，解题的关键是熟练掌握二次根式混合运算法则．

18. 如图，平面直角坐标系中有一个，顶点A，B，C．

（1）画出关于y轴的对称图形（不写画法）：

（2）若P是y轴上的动点，则的最小值为             ；

（3）若网格上的每个小正方形的边长为1，则的面积是           ．

【答案】（1）见解析    （2）   

（3）

【解析】

【分析】（1）确定各顶点关于y轴对称的对称点位置，再连接即可；

（2）画出图形确定点P坐标，进而解答即可；

（3）将周边围矩形，用矩形面积减去三个直角三角形的面积，即可求得的面积．

【小问1详解】

解：如图所示：

【小问2详解】

解： ，

的最小值为

【小问3详解】

解：的面积=

【点睛】本题主要考查了轴对称变换的作图，熟知轴对称的性质是解答此题的关键．

19. 如图，有一张三角形纸片，三边长分别为，，．

（1）求证：；

（2）将沿折叠，使点B与点A重合，求的长．

【答案】（1）见解析    （2）

【解析】

【分析】（1）根据勾股定理的逆定理证明为直角三角形，即可得出答案；

（2）由折叠知：，设，则，根据勾股定理列出关于x的方程，解方程即可得出答案．

【小问1详解】

证明：∵中，，，，

∴，，，

∴，

∴为直角三角形，

即；

【小问2详解】

解：由折叠知：，为直角三角形，

在中，①，

设，则，

代入①式得

化简得，

解得：，

即CD的长为．

【点睛】本题主要考查了勾股定理及其逆定理，解题的关键是熟练掌握勾股定理及其逆定理．

20. 如图，直线与x轴相交于点A，与y轴相交于点B．

（1）求A，B两点的坐标；

（2）x轴上有一点P，且，求的面积．

【答案】（1），   

（2）的面积为4或12

【解析】

【分析】（1）利用一次函数图象上点的坐标特征可求出点A、B的坐标．

（2）由点A、B的坐标得出OA的，OB的长，结合OP=2OA可得出P点坐标，进而求出AP的长，再利用三角形的面积公式求出面积．

【小问1详解】

∵直线交x轴于点A，交y轴于点B，

∴设A点坐标为，B点坐标为，

∴代入，

解得：，，

∴，

【小问2详解】

∵，，

∴，

∴P点坐标为或，

∴或6，

∴或，

∴的面积为4或12．

【点睛】本题考查了一次函数图象上点的坐标特征及三角形的面积，牢记直线上任意一点的坐标都满足函数解析式以及三角形的面积公式是解题的关键．

21. 如图，在平面直角坐标系中，过点的直线与直线相交于点
 

（1）求直线及直线的函数表达式；

（2）求的面积；

（3）填空：__________．

【答案】（1），   

（2）6    （3）

【解析】

【分析】（1）用待定系数法求解解析式即可

（2）根据解析式求出B点的坐标，根据点A和点B坐标，计算面积

（3）根据已知点的坐标，计算线段的长度即可

【小问1详解】

解：设直线OA的解析式为，

∵点，

∴，

解得

∴直线的解析式为；

设直线的解析式为，

∵点，点在直线AB上，

∴，

解得：，

∴直线的解析式为

小问2详解】

∵直线的解析式为，

∴，

∴

∴

即的面积为6；

【小问3详解】

∵，

∴

【点睛】本题主要考查一次函数的图像和性质，熟练掌握待定系数法求解析式及一次函数的图像和性质是解题的关键

22. 如图1，长方形OABC的边OA、OC分别在x轴、y轴上，B点坐标是（8，4），将△AOC沿对角线AC翻折得△ADC，AD与BC相交于点E．

（1）求证：△CDE≌△ABE

（2）求E点坐标；

（3）如图2，动点P从点A出发，沿着折线A→B→C→O运动（到点O停止），是否存在点P，使得△POA的面积等于△ACE的面积，若存在，直接写出点P坐标，若不存在，说明理由．

【答案】(1)见解析；（2）E（5，4）；（3）存在，满足条件的点P的坐标为（8，）或（0，），理由见解析

【解析】

【分析】（1）用角角边定理即可证明．
（2）设CE=AE=n，则BE=8-n，利用勾股定理即可求解．
（3）构建方程确定点P的纵坐标即可解决问题．

【详解】解：（1）证明：∵四边形OABC为矩形，

∴AB＝OC，∠B＝∠AOC＝90°，

∴CD＝OC＝AB，∠D＝∠AOC＝∠B，

又∠CED＝∠ABE，

∴△CDE≌△ABE（AAS），

∴CE＝AE；

（2）∵B（8，4），即AB＝4，BC＝8．

∴设CE＝AE＝n，则BE＝8﹣n，

可得（8﹣n）2+42＝n2，

解得：n＝5，

∴E（5，4）；

（3）∵S△ACE＝•CE•AB＝×5×4＝10，

∴S△POA＝•OA•yP＝10，

∴×8×yP＝10，

∴yP＝，

∴满足条件的点P的坐标为（8，）或（0，）．

【点睛】本题属于四边形综合题，考查了翻折变换，矩形的性质，三角形的面积等知识，解题的关键是学会两条城市构建方程解决问题，属于中考常考题型．

23. 如图，直线l： 交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．

（1）点A坐标是       ，点B的坐标        ，BC=       ．

（2）当点P在什么位置时，△APQ≌△CBP，说明理由．

（3）当△PQB为等腰三角形时，求点P的坐标．

【答案】（1），，   

（2）   

（3）的坐标为，

【解析】

【分析】（1）对于直线l解析式，分别令x与y为0求出y与x的值，确定出A与B的坐标，根据A与C关于y轴对称确定出C坐标，利用勾股定理求出BC的长即可；

（2）由三角形APQ与三角形CBP全等，利用全等三角形对应边相等得到，由，求出OP的长，确定出P坐标即可；

（3）分三种情况考虑：当时，由（2）确定出此时P的坐标；当时，利用外角性质判断不可能；当时，求出此时P的坐标即可．

【小问1详解】

对于直线l：，

令，得到；令，得到，

∴，，即，

∵A与C关于y轴对称，

∴，即，

则根据勾股定理得：；

【小问2详解】

由，得到，

∵，即，

∴，即；

【小问3详解】

（i）当时，，

由（2）知此时点；

（ii）当时，，

∵是的外角，

∴，

又∵，

∴这种情况不可能；

（iii）当时，，

又∵，

∴，

∴，，

∴，

解得：．

此时点P的坐标为：．

综上，P的坐标为，．