
辽宁省本溪市2021-2023三年中考数学真题分类汇编-03解答题(提升题)知识点分类
展开辽宁省本溪市2021-2023三年中考数学真题分类汇编-03解答题(提升题)知识点分类
一.一元一次不等式的应用(共1小题)
1.(2023•辽宁)某礼品店经销A,B两种礼品盒,第一次购进A种礼品盒10盒,B种礼品盒15盒,共花费2800元;第二次购进A种礼品盒6盒,B种礼品盒5盒,共花费1200元.
(1)求购进A,B两种礼品盒的单价分别是多少元;
(2)若该礼品店准备再次购进两种礼品盒共40盒,总费用不超过4500元,那么至少购进A种礼品盒多少盒?
二.二次函数综合题(共3小题)
2.(2023•辽宁)如图,抛物线y=﹣x2+bx+c与x轴交于点A和点B(4,0),与y轴交于点C(0,4),点E在抛物线上.
(1)求抛物线的解析式;
(2)点E在第一象限内,过点E作EF∥y轴,交BC于点F,作EH∥x轴,交抛物线于点H,点H在点E的左侧,以线段EF,EH为邻边作矩形EFGH,当矩形EFGH的周长为11时,求线段EH的长;
(3)点M在直线AC上,点N在平面内,当四边形OENM是正方形时,请直接写出点N的坐标.
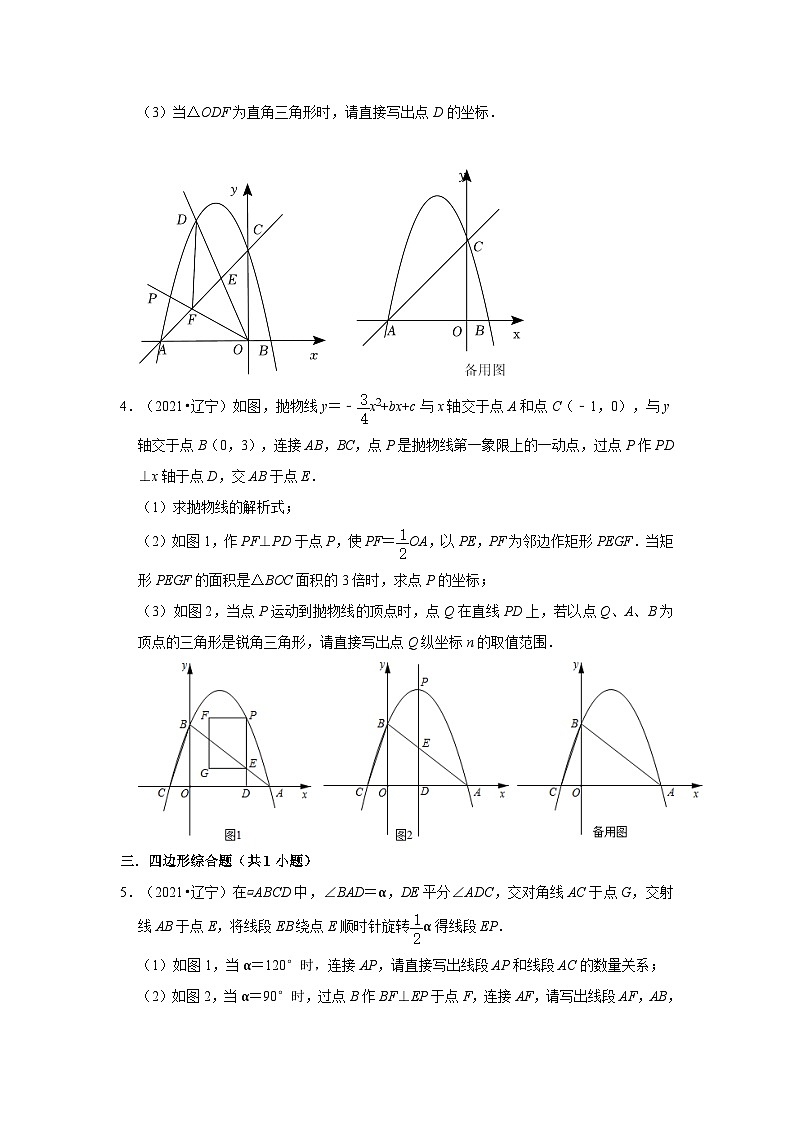
3.(2022•辽宁)如图,抛物线y=ax2﹣3x+c与x轴交于A(﹣4,0),B两点,与y轴交于点C(0,4),点D为x轴上方抛物线上的动点,射线OD交直线AC于点E,将射线OD绕点O逆时针旋转45°得到射线OP,OP交直线AC于点F,连接DF.
(1)求抛物线的解析式;
(2)当点D在第二象限且=时,求点D的坐标;
(3)当△ODF为直角三角形时,请直接写出点D的坐标.
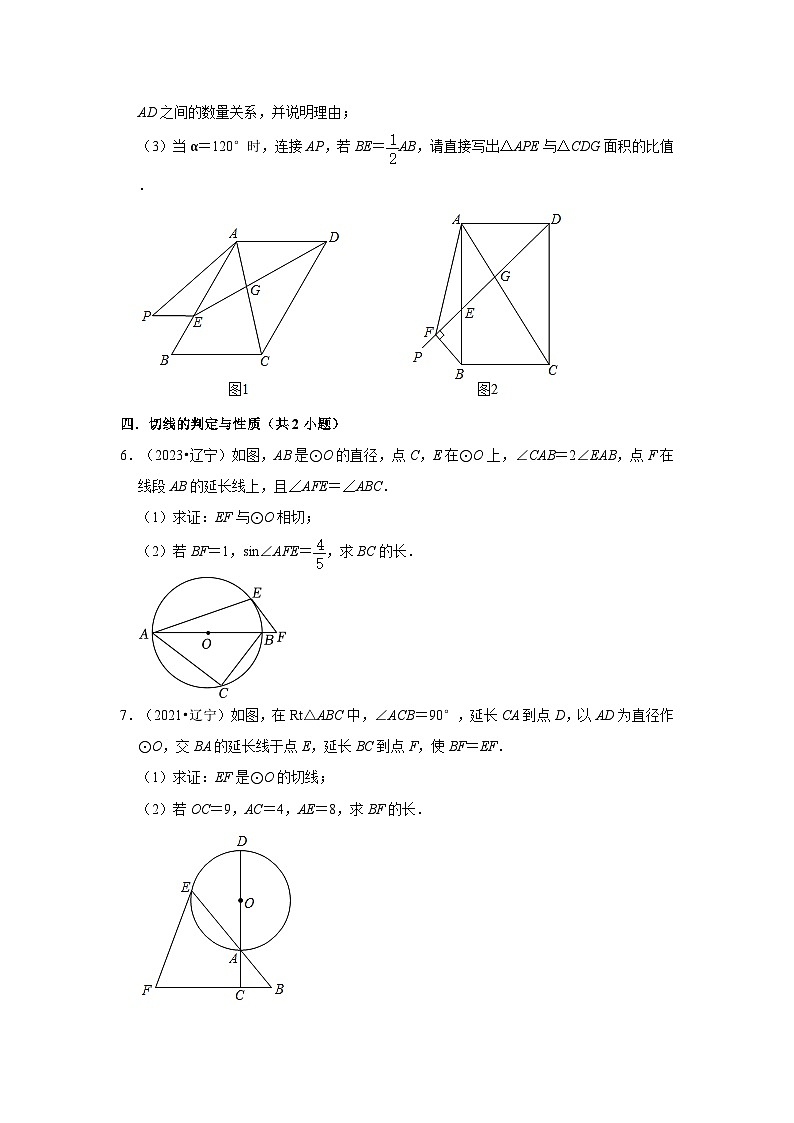
4.(2021•辽宁)如图,抛物线y=﹣x2+bx+c与x轴交于点A和点C(﹣1,0),与y轴交于点B(0,3),连接AB,BC,点P是抛物线第一象限上的一动点,过点P作PD⊥x轴于点D,交AB于点E.
(1)求抛物线的解析式;
(2)如图1,作PF⊥PD于点P,使PF=OA,以PE,PF为邻边作矩形PEGF.当矩形PEGF的面积是△BOC面积的3倍时,求点P的坐标;
(3)如图2,当点P运动到抛物线的顶点时,点Q在直线PD上,若以点Q、A、B为顶点的三角形是锐角三角形,请直接写出点Q纵坐标n的取值范围.
三.四边形综合题(共1小题)
5.(2021•辽宁)在▱ABCD中,∠BAD=α,DE平分∠ADC,交对角线AC于点G,交射线AB于点E,将线段EB绕点E顺时针旋转α得线段EP.
(1)如图1,当α=120°时,连接AP,请直接写出线段AP和线段AC的数量关系;
(2)如图2,当α=90°时,过点B作BF⊥EP于点F,连接AF,请写出线段AF,AB,AD之间的数量关系,并说明理由;
(3)当α=120°时,连接AP,若BE=AB,请直接写出△APE与△CDG面积的比值.
四.切线的判定与性质(共2小题)
6.(2023•辽宁)如图,AB是⊙O的直径,点C,E在⊙O上,∠CAB=2∠EAB,点F在线段AB的延长线上,且∠AFE=∠ABC.
(1)求证:EF与⊙O相切;
(2)若BF=1,sin∠AFE=,求BC的长.
7.(2021•辽宁)如图,在Rt△ABC中,∠ACB=90°,延长CA到点D,以AD为直径作⊙O,交BA的延长线于点E,延长BC到点F,使BF=EF.
(1)求证:EF是⊙O的切线;
(2)若OC=9,AC=4,AE=8,求BF的长.
五.几何变换综合题(共2小题)
8.(2022•辽宁)在△ABC中,∠BAC=90°,AB=AC,线段AB绕点A逆时针旋转至AD(AD不与AC重合),旋转角记为α,∠DAC的平分线AE与射线BD相交于点E,连接EC.
(1)如图①,当α=20°时,∠AEB的度数是 ;
(2)如图②,当0°<α<90°时,求证:BD+2CE=AE;
(3)当0°<α<180°,AE=2CE时,请直接写出的值.
9.(2023•辽宁)在Rt△ABC中,∠ACB=90°,CA=CB,点O为AB的中点,点D在直线AB上(不与点A,B重合),连接CD,线段CD绕点C逆时针旋转90°,得到线段CE,过点B作直线l⊥BC,过点E作EF⊥l,垂足为点F,直线EF交直线OC于点G.
(1)如图1,当点D与点O重合时,请直接写出线段AD与线段EF的数量关系;
(2)如图2,当点D在线段AB上时,求证:CG+BD=BC;
(3)连接DE,△CDE的面积记为S1,△ABC的面积记为S2,当EF:BC=1:3时,请直接写出的值.
六.解直角三角形的应用-坡度坡角问题(共1小题)
10.(2023•辽宁)暑假期间,小明与小亮相约到某旅游风景区登山.需要登顶600m高的山峰,由山底A处先步行300m到达B处,再由B处乘坐登山缆车到达山顶D处.已知点A,B,D,E,F在同一平面内,山坡AB的坡角为30°,缆车行驶路线BD与水平面的夹角为53°(换乘登山缆车的时间忽略不计).
(1)求登山缆车上升的高度DE;
(2)若步行速度为30m/min,登山缆车的速度为60m/min,求从山底A处到达山顶D处大约需要多少分钟(结果精确到0.1min).
(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
七.列表法与树状图法(共2小题)
11.(2023•辽宁)6月5日是世界环境日,为提高学生的环保意识,某校举行了环保知识竞赛,从全校学生的成绩中随机抽取了部分学生的成绩进行分析,把结果划分为4个等级:A(优秀);B(良好);C(中);D(合格).并将统计结果绘制成如图两幅统计图.
请根据统计图提供的信息,解答下列问题:
(1)本次抽样调查的学生共有 名;
(2)补全条形统计图;
(3)该校共有1200名学生,请你估计本次竞赛获得B等级的学生有多少名?
(4)在这次竞赛中,九年一班共有4人获得了优秀,4人中有两名男同学,两名女同学,班主任决定从这4人中随机选出2人在班级为其他同学做培训,请你用列表法或画树状图法,求所选2人恰好是一男一女的概率.
12.(2021•辽宁)为迎接建党100周年,某校组织学生开展了党史知识竞赛活动.竞赛项目有:A.回顾重要事件;B.列举革命先烈;C.讲述英雄故事;D.歌颂时代精神.学校要求学生全员参加且每人只能参加一项,为了解学生参加竞赛情况,随机调查了部分学生,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)本次被调查的学生共有 名;
(2)在扇形统计图中“B项目”所对应的扇形圆心角的度数为 ,并把条形统计图补充完整;
(3)从本次被调查的小华、小光、小艳、小萍这四名学生中,随机抽出2名同学去做宣讲员,请用列表或画树状图的方法求出恰好小华和小艳被抽中的概率.
辽宁省本溪市2021-2023三年中考数学真题分类汇编-03解答题(提升题)知识点分类
参考答案与试题解析
一.一元一次不等式的应用(共1小题)
1.(2023•辽宁)某礼品店经销A,B两种礼品盒,第一次购进A种礼品盒10盒,B种礼品盒15盒,共花费2800元;第二次购进A种礼品盒6盒,B种礼品盒5盒,共花费1200元.
(1)求购进A,B两种礼品盒的单价分别是多少元;
(2)若该礼品店准备再次购进两种礼品盒共40盒,总费用不超过4500元,那么至少购进A种礼品盒多少盒?
【答案】(1)购买每盒A种礼品盒要100元,每盒B种礼品盒要120元;
(2)最少需要购买15个A种礼品盒.
【解答】解:(1)设购买每盒A种礼品盒要x元,每盒B种礼品盒要y元,由题意得,
,
解得:,
答:购买每盒A种礼品盒要100元,每盒B种礼品盒要120元;
(2)设需要购买m个A种礼品盒,则购买(40﹣m)个B种礼品盒,由题意得,
100m+120(40﹣m)≤4500,
解得:m≥15,
答:最少需要购买15个A种礼品盒.
二.二次函数综合题(共3小题)
2.(2023•辽宁)如图,抛物线y=﹣x2+bx+c与x轴交于点A和点B(4,0),与y轴交于点C(0,4),点E在抛物线上.
(1)求抛物线的解析式;
(2)点E在第一象限内,过点E作EF∥y轴,交BC于点F,作EH∥x轴,交抛物线于点H,点H在点E的左侧,以线段EF,EH为邻边作矩形EFGH,当矩形EFGH的周长为11时,求线段EH的长;
(3)点M在直线AC上,点N在平面内,当四边形OENM是正方形时,请直接写出点N的坐标.
【答案】(1)见解答.
(2)EH=4,
(3)点N的坐标为(4,4)或(﹣,)或(,)或(,).
【解答】解:(1)∵抛物线y=﹣x2+bx+c经过点B(4,0)和C(0,4),
∴
解得,
∴抛物线的解析式为y=﹣x2+x+4;
(2)∵点B(4,0)和C(0,4).
设直线BC的解析式为y=kx+4,则0=4k+4,
解得k=﹣1.
直线BC的解析式为y=﹣x+4,
设E(x,﹣x2+x+4),且0<x<4,则F(x,﹣x+4),
GH=EF=﹣x2+x+4﹣(﹣x+4)=﹣x2+2x,
∵抛物线的对称轴为直线x=﹣,
∴H(2﹣x,﹣x2+x+4),
∴GF=EH=x﹣(2﹣x)=2x﹣2,
依题意得2(﹣x2+2x+2x﹣2)=11.
解得x=5(舍去)或x=3.
∴EH=4,
(3)令y=0,则﹣x2+x+4=0,
解得x=﹣2或x=4.
∴A(﹣2,0).
设直线AC的解析式为y=px+q,将A(﹣2,0),C(0,4)代入,
解得p=2,q=4,
∴直线AC的解析式为y=2x+4,
∵四边形OENM是正方形,
∴OE=OM,∠EOM=90°,分别过点M、E作y轴的垂线,垂足分别为P、Q,如图,
∠OPM=∠EQO=90°,∠OMP=90°﹣∠MOP=∠EOQ.
∴△OMP≌Δ EOQ(AAS).
∴PM=OQ,PO=EQ.
设E(m,﹣m2+m+4),
:∴PO=EQ=﹣m,PM=OQ=m2﹣m﹣4.则M(m2﹣m﹣4,m),
∵点M在直线AC上,
∴m=2(﹣m﹣4)+4.
解得m=4或m=﹣1,
当m=4时,M(0,4),E(4,0),
即点M与点C重合,点E与点B重合时,四边形OENM是正方形,此时N(4,4):
当m=﹣1时,M(﹣,﹣1),E(﹣1,),
点O向左平移个单位,再向下平移1个单位,得到点M,
则点E向左平移个单位,再向下平移1个单位,得到点N,
N(﹣1﹣,﹣1),即N(﹣,).
当OM沿着点O逆时针旋转90°得到OE,如图:
设M(a,b),则点E(b,﹣a),
∵点M在y=2x+4的图象上,
∴b=2a+4,则点M(a,2a+4),
此时点E(2a+4,﹣a),
点E在y=﹣x2+x+4的图象上,
∴,
解得a=0或﹣,
∴M1 (0,4),E1 (4,0),M2(﹣,﹣1),E2(﹣1,),
当点E为点M绕点O逆时针旋转90°时,点E(﹣b,a),
M(a,2a+4),E(﹣2a﹣4,a),
点E在y=﹣x2+x+4的图象上,
∴﹣(﹣2a﹣4)2﹣2a﹣4+4=a,
解得a=,
∴M1(,),E1(,),
M2(,),E2(,),
∴点N的坐标为(,)或(,),
综上,点N的坐标为(4,4)或(﹣,)或(,)或(,).
3.(2022•辽宁)如图,抛物线y=ax2﹣3x+c与x轴交于A(﹣4,0),B两点,与y轴交于点C(0,4),点D为x轴上方抛物线上的动点,射线OD交直线AC于点E,将射线OD绕点O逆时针旋转45°得到射线OP,OP交直线AC于点F,连接DF.
(1)求抛物线的解析式;
(2)当点D在第二象限且=时,求点D的坐标;
(3)当△ODF为直角三角形时,请直接写出点D的坐标.
【答案】(1)y=﹣x2﹣3x+4;
(2)(﹣1,6)或(﹣3,4);
(3)(,2)或(,2)或(0,4)或(﹣3,4).
【解答】解:(1)将点A(﹣4,0),C(0,4)代入y=ax2﹣3x+c,
∴,
解得,
∴y=﹣x2﹣3x+4;
(2)过点D作DG⊥AB交于G,交AC于点H,
设直线AC的解析式为y=kx+b,
∴,
解得,
∴y=x+4,
设D(n,﹣n2﹣3n+4),H(n,n+4),
∴DH=﹣n2﹣4n,
∵DH∥OC,
∴==,
∵OC=4,
∴DH=3,
∴﹣n2﹣4n=3,
解得n=﹣1或n=﹣3,
∴D(﹣1,6)或(﹣3,4);
(3)设F(t,t+4),
当∠FDO=90°时,过点D作MN⊥y轴交于点N,过点F作FM⊥MN交于点M,
∵∠DOF=45°,
∴DF=DO,
∵∠MDF+∠NDO=90°,∠MDF+∠MFD=90°,
∴∠NDO=∠MFD,
∴△MDF≌△NOD(AAS),
∴DM=ON,MF=DN,
∴DN+ON=﹣t,DN=ON+(﹣t﹣4),
∴DN=﹣t﹣2,ON=2,
∴D点纵坐标为2,
∴﹣x2﹣3x+4=2,
解得x=或x=,
∴D点坐标为(,2)或(,2);
当∠DFO=90°时,过点F作KL⊥x轴交于L点,过点D作DK⊥KL交于点K,
∵∠KFD+∠LFO=90°,∠KFD+∠KDF=90°,
∴∠LFO=∠KDF,
∵DF=FO,
∴△KDF≌△LFO(AAS),
∴KD=FL,KF=LO,
∴KL=t+4﹣t=4,
∴D点纵坐标为4,
∴﹣x2﹣3x+4=4,
解得x=0或x=﹣3,
∴D(0,4)或(﹣3,4);
综上所述:D点坐标为(,2)或(,2)或(0,4)或(﹣3,4).
4.(2021•辽宁)如图,抛物线y=﹣x2+bx+c与x轴交于点A和点C(﹣1,0),与y轴交于点B(0,3),连接AB,BC,点P是抛物线第一象限上的一动点,过点P作PD⊥x轴于点D,交AB于点E.
(1)求抛物线的解析式;
(2)如图1,作PF⊥PD于点P,使PF=OA,以PE,PF为邻边作矩形PEGF.当矩形PEGF的面积是△BOC面积的3倍时,求点P的坐标;
(3)如图2,当点P运动到抛物线的顶点时,点Q在直线PD上,若以点Q、A、B为顶点的三角形是锐角三角形,请直接写出点Q纵坐标n的取值范围.
【答案】(1)y=﹣x2+x+3;(2)点P的坐标为(1,)或(3,3);(3)﹣<n<或<n<5.
【解答】解:(1)由题意得:,解得,
故抛物线的表达式为y=﹣x2+x+3;
(2)对于y=﹣x2+x+3,令y=﹣x2+x+3=0,解得x=4或﹣1,
故点A的坐标为(4,0),则PF=2,
由点A、B的坐标得,直线AB的表达式为y=﹣x+3,
设点P的坐标为(x,﹣x2+x+3),则点E(x,﹣x+3),
则矩形PEGF的面积=PF•PE=2×(﹣x2+x+3+x﹣3)=3S△BOC=3××BO•CO=×3×1,
解得x=1或3,
故点P的坐标为(1,)或(3,3);
(3)由抛物线的表达式知,其对称轴为x=,故点Q的坐标为(,n),
当∠ABQ为直角时,如图2﹣1,
设BQ交x轴于点H,
由直线AB的表达式知,tan∠BAO=,则tan∠BHO=,
故设直线BQ的表达式为y=x+t,
该直线过点B(0,3),故t=3,
则直线BQ的表达式为y=x+3,
当x=时,y=x+3=5,
即n=5;
②当∠BQA为直角时,
过点Q作直线MN交y轴于点N,交过点A与y轴的平行线于点M,
∵∠BQN+∠MQA=90°,∠MQA+∠MAQ=90°,
∴∠BQN=∠MAQ,
∴tan∠BQN=tan∠MAQ,
即,则,
解得n=;
③当∠BAQ为直角时,
同理可得,n=﹣;
综上,以点Q、A、B为顶点的三角形是锐角三角形,则△ABQ不为直角三角形,
故点Q纵坐标n的取值范围为﹣<n<或<n<5.
三.四边形综合题(共1小题)
5.(2021•辽宁)在▱ABCD中,∠BAD=α,DE平分∠ADC,交对角线AC于点G,交射线AB于点E,将线段EB绕点E顺时针旋转α得线段EP.
(1)如图1,当α=120°时,连接AP,请直接写出线段AP和线段AC的数量关系;
(2)如图2,当α=90°时,过点B作BF⊥EP于点F,连接AF,请写出线段AF,AB,AD之间的数量关系,并说明理由;
(3)当α=120°时,连接AP,若BE=AB,请直接写出△APE与△CDG面积的比值.
【答案】(1)AP=AC;
(2)AB2+AD2=2AF2;理由见解答;
(3)或.
【解答】解:(1)方法一:如图1,连接PB,PC,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC,
∵α=120°,即∠BAD=120°,
∴∠B=∠ADC=60°,
∴∠BEP=60°=∠B,
由旋转知:EP=EB,
∴△BPE是等边三角形,
∴BP=EP,∠EBP=∠BPE=60°,
∴∠CBP=∠ABC+∠EBP=120°,
∵∠AEP=180°﹣∠BEP=120°,
∴∠AEP=∠CBP,
∵DE平分∠ADC,
∴∠ADE=∠CDE=30°,
∴∠AED=∠CDE=30°=∠ADE,
∴AD=AE,
∴AE=BC,
∴△APE≌△CPB(SAS),
∴AP=CP,∠APE=∠CPB,
∴∠APE+∠CPE=∠CPB+∠CPE,
即∠APC=∠BPE=60°,
∴△APC是等边三角形,
∴AP=AC;
方法二:如图1,延长PE交CD于点Q,连接AQ,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∵α=120°,即∠BAD=120°,
∴∠B=∠ADC=60°,
∴∠BEP=60°=∠B,
∴PE∥BC∥AD,
∴四边形ADQE和四边形BCQE是平行四边形,
∵DE平分∠ADC,
∴∠ADE=∠CDE=30°,
∴∠AED=∠CDE=30°=∠ADE,
∴AD=AE,
∴四边形ADQE是菱形,
∴∠EAQ=∠AEQ=60°,
∴△AEQ是等边三角形,
∴AE=AQ,∠AQE=60°,
∵四边形BCQE是平行四边形,
∴PE=BE=CQ,∠B=∠CQE=60°,
∵∠AEP=120°,∠AQC=∠AQE+∠CQE=120°,
∴∠AEP=∠AQC,
∴△AEP≌△AQC(SAS),
∴AP=AC;
(2)AB2+AD2=2AF2,
理由:如图2,连接CF,
在▱ABCD中,∠BAD=90°,
∴∠ADC=∠ABC=∠BAD=90°,AD=BC,
∵DE平分∠ADC,
∴∠ADE=∠CDE=45°,
∴∠AED=∠ADE=45°,
∴AD=AE,
∴AE=BC,
∵BF⊥EP,
∴∠BFE=90°,
∵∠BEF=α=∠BAD=×90°=45°,
∴∠EBF=∠BEF=45°,
∴BF=EF,
∵∠FBC=∠FBE+∠ABC=45°+90°=135°,
∠AEF=180°﹣∠FEB=135°,
∴∠CBF=∠AEF,
∴△BCF≌△EAF(SAS),
∴CF=AF,∠CFB=∠AFE,
∴∠AFC=∠AFE+∠CFE=∠CFB+∠CFE=∠BFE=90°,
∴∠ACF=∠CAF=45°,
∵sin∠ACF=,
∴AC====AF,
在Rt△ABC中,AB2+BC2=AC2,
∴AB2+AD2=2AF2;
(3)方法一:由(1)知,BC=AD=AE=AB﹣BE,
∵BE=AB,AB=CD,
∴AB=CD=2BE,
设BE=a,则PE=AD=AE=a,AB=CD=2a,
①当点E在AB上时,如图3,过点G作GM⊥AD于点M,作GN⊥CD于点N,
过点C作CK⊥AD于点K,过点A作AH⊥PE的延长线于点H,
当α=120°时,∠B=∠ADC=60°,
∵DE平分∠ADC,GM⊥AD,GN⊥CD,
∴GM=GN,
∵S△ACD=AD•CK=a•2a•sin60°=a2,
====2,
∴S△CDG=2S△ADG,
∴S△CDG=S△ACD=a2,
由(1)知PE∥BC,
∴∠AEH=∠B=60°,
∵∠H=90°,
∴AH=AE•sin60°=a,
∴S△APE=PE•AH=a•a=a2,
∴==.
②如图4,当点E在AB延长线上时,
由①同理可得:S△CDG=S△ACD=××2a××3a=a2,
S△APE=PH•AE=×a×3a=a2,
∴==,
综上所述,△APE与△CDG面积的比值为或.
方法二:如图3,∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴△AEG∽△CDG,
∴=()2,=,
①当点E在AB上时,
∵BE=AB,
∴AE=BE=AB=CD,
∴=()2=,
又∵==,
∴=,即=3,
∴==3,
当α=120°时,∠B=∠ADC=60°,
∵DE平分∠ADC,
∴∠ADE=30°,
∴∠AED=180°﹣∠BAD﹣∠ADE=30°=∠ADE,
∴AE=AD,
∵EP=EB=AE,EP∥AD,
∴EP=AD=AE,∠AEP=∠DAE=120°,
∴△AED≌△EAP(SAS),
∴S△AED=S△EAP,
∴=•=•=3×=;
②如图4,当点E在AB延长线上时,
∵BE=AB,
∴AE=AB=CD,
由①知,AD=AE=CD,
∵EP=BE=AE=AD,EP∥AD,
∴==,
∵==,
∴=,
∴==,
∵=()2=()2=,
∴=••=××=;
综上所述,△APE与△CDG面积的比值为或.
四.切线的判定与性质(共2小题)
6.(2023•辽宁)如图,AB是⊙O的直径,点C,E在⊙O上,∠CAB=2∠EAB,点F在线段AB的延长线上,且∠AFE=∠ABC.
(1)求证:EF与⊙O相切;
(2)若BF=1,sin∠AFE=,求BC的长.
【答案】(1)详见解答;
(2).
【解答】(1)证明:如图,连接OE,
∵OA=OE,
∴∠OAE=∠OEA,
∴∠FOE=∠OAE+∠OEA=2∠OAE,
∵∠CAB=2∠EAB,
∴∠CAB=∠FOE,
又∵∠AFE=∠ABC,
∴∠CAB+∠ABC=∠FOE+∠AFE,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°=∠FOE+∠AFE,
∴∠OEF=90°,
即OE⊥EF,
∵OE是半径,
∴EF是⊙O的切线;
(2)解:在Rt△EOF中,设半径为r,即OE=OB=r,则OF=r+1,
∵sin∠AFE===,
∴r=4,
∴AB=2r=8,
在Rt△ABC中,sin∠ABC==sin∠AFE=,AB=8,
∴AC=×8=,
∴BC==.
7.(2021•辽宁)如图,在Rt△ABC中,∠ACB=90°,延长CA到点D,以AD为直径作⊙O,交BA的延长线于点E,延长BC到点F,使BF=EF.
(1)求证:EF是⊙O的切线;
(2)若OC=9,AC=4,AE=8,求BF的长.
【答案】(1)见解析;
(2).
【解答】证明:(1)连接OE,
∵OA=OE,
∴∠OEA=∠OAE,
在Rt△ABC中,∠ACB=90°,
∴∠BAC+∠B=90°,
∵BF=EF,
∴∠B=∠BEF,
∵∠OAE=∠BAC,
∴∠OEA=∠BAC,
∴∠OEF=∠OEA+∠BEF=∠BAC+∠B=90°,
∴OE⊥EF,
∵OE是⊙O的半径,
∴EF是⊙O的切线;
(2)解:连接DE,
∵OC=9,AC=4,
∴OA=OC﹣AC=5,
∵AD=2OA,
∴AD=10,
∵AD是⊙O的直径,
∴∠AED=90°,
在Rt△ADE中,
∵DE===6,
∴cos∠DAE===,
在Rt△ABC中,cos∠BAC==,
∵∠BAC=∠DAE,
∴=,
∴AB=5,
∴BE=AB+AE=5+8=13,
∵OD=OE,
∴∠ODE=∠OED,
∵EF是⊙O的切线,
∴∠FEO=90°,
∵∠OED+∠OEA=90°,∠FEB+∠OEA=90°,
∴∠FEB=∠OED,
∴∠B=∠FEB=∠OED=∠ODE,
∴△FBE∽△ODE,
∴=,
∴=,
∴BF=.
方法二:解:连接DE,
∵OC=9,AC=4,
∴OA=OC﹣AC=5,
∵AD=2OA,
∴AD=10,
∵AD是⊙O的直径,
∴∠AED=90°,
在Rt△ADE中,
∵DE===6,
∴cos∠DAE===,
在Rt△ABC中,cos∠BAC==,
∵∠BAC=∠DAE,
∴=,
∴AB=5,
∴BE=AB+AE=5+8=13,
过F作FH⊥BE于F,
则BH=6.5,
∵∠B的余弦等于0.6,
∴BF=6.5÷0.6=.
五.几何变换综合题(共2小题)
8.(2022•辽宁)在△ABC中,∠BAC=90°,AB=AC,线段AB绕点A逆时针旋转至AD(AD不与AC重合),旋转角记为α,∠DAC的平分线AE与射线BD相交于点E,连接EC.
(1)如图①,当α=20°时,∠AEB的度数是 45° ;
(2)如图②,当0°<α<90°时,求证:BD+2CE=AE;
(3)当0°<α<180°,AE=2CE时,请直接写出的值.
【答案】(1)45°;
(2)证明见解析;
(3)2+2或2﹣2.
【解答】(1)解:∵线段AB绕点A逆时针旋转α至AD,α=20°,
∴∠BAD=20°,AB=AD,
∴∠ADB=∠ABD=×(180°﹣20°)=80°,
又∵∠BAC=90°,
∴∠DAC=70°,
∵AE平分∠DAC,
∴∠DAE=∠DAC=35°,
∴∠AEB=∠ADB﹣∠DAE=80°﹣35°=45°,
故答案为:45°;
(2)证明:延长DB到F,使BF=CE,连接AF,
∵AB=AC,AD=AB,
∴AD=AC,
∵AE平分∠DAC,
∴∠DAE=∠CAE,
又∵AE=AE,
∴△ADE≌△ACE(SAS),
∴∠DEA=∠CEA,∠ADE=∠ACE,DE=CE,
∵AB=AD,
∴∠ABD=∠ADB,
∵∠ADE+∠ADB=180°,
∴∠ACE+∠ABD=180°,
∵∠BAC=90°,
∴∠BEC=360°﹣(∠ACE+∠ABD)﹣∠BAC=360°﹣180°﹣90°=90°,
∵∠DEA=∠CEA,
∴∠DEA=∠CEA=90°=45°,
∵∠ABF+∠ABD=180°,∠ACE+∠ABD=180°,
∴∠ABF=∠ACE,
∵AB=AC,BF=CE,
∴△ABF≌△ACE(SAS),
∴AF=AE,∠AFB=∠AEC=45°,
∴∠FAE=180°﹣45°﹣45°=90°,
在Rt△AFE中,∠FAE=90°,
∵cos∠AEF=,
∴EF=,
∵EF=BF+BD+DE=CE+BD+CE=BD+2CE,
∴BD+2CE=AE;
(3)解:如图3,当0°<α<90°时,
由(2)可知BD+2CE=AE,CE=DE,
∵AE=2CE,
∴BD+2DE=2DE,
∴=2;
如图4,当90°<α<180°时,
在BD上截取BF=DE,连接AF,方法同(2)可证△ADE≌△ACE(SAS),
∴DE=CE,
∵AB=AC=AD,
∴∠ABF=∠ADE,
∴△ABF≌△ADE(SAS),
∴AF=AE,∠BAF=∠DAE,
又∵∠DAE=∠CAE,
∴∠BAF=∠CAE,
∴∠EAF=∠FAC+∠CAE=∠FAC+∠BAF=∠BAC=90°,
∴△AEF是等腰直角三角形,
∴EF=AE,
∴BD=BF+DE+EF=2DE+AE,
∵AE=2CE=2DE,
∴BD=2DE+2DE,
∴+2.
综上所述,的值为2+2或2﹣2.
9.(2023•辽宁)在Rt△ABC中,∠ACB=90°,CA=CB,点O为AB的中点,点D在直线AB上(不与点A,B重合),连接CD,线段CD绕点C逆时针旋转90°,得到线段CE,过点B作直线l⊥BC,过点E作EF⊥l,垂足为点F,直线EF交直线OC于点G.
(1)如图1,当点D与点O重合时,请直接写出线段AD与线段EF的数量关系;
(2)如图2,当点D在线段AB上时,求证:CG+BD=BC;
(3)连接DE,△CDE的面积记为S1,△ABC的面积记为S2,当EF:BC=1:3时,请直接写出的值.
【答案】(1)AD=EF,理由见解答过程;
(2)证明见解答过程;
(3)的值为或.
【解答】(1)解:AD=EF,理由如下:
连接BE,如图:
∵∠ACB=90°,CA=CB,
∴∠A=45°,
∵线段CD绕点C逆时针旋转90°,得到线段CE,
∴CD=CE,∠DCE=90°,
∴∠BCE=90°﹣∠BCD=∠ACD,
∴△BCE≌△ACD(SAS),
∴BE=AD,∠A=∠CBE=45°,
∵直线l⊥BC,
∴∠EBF=45°,
∴△BEF是等腰直角三角形,
∴BE=EF,
∴AD=EF;
(2)证明:如图,
∵∠ACB=90°,CA=CB,O为AB的中点,
∴∠COB=90°,AB=BC,
∵∠BFG=90°,
∴∠G=360°﹣∠COB﹣∠OBF﹣∠BFG=45°=∠A,
∵BC⊥直线l,EF⊥直线l,
∴BC∥GF,
∴∠CEG=∠BCE,
∵∠BCE=90°﹣∠BCD=∠ACD,
∴∠CEG=∠ACD,
∵CE=CD,
∴△CEG≌△DCA(AAS),
∴CG=AD,
∵AD+BD=AB,
∴CG+BD=BC;
(3)解:由EF:BC=1:3,设EF=m,则BC=AC=3m,
当D在线段AB上时,延长AC交GF于K,如图:
由(2)知△CEG≌△DCA,
∴GE=AC=3m,
∵∠CBF=∠BFE=∠BCK=90°,
∴四边形BCKF是矩形,
∴KF=BC=3m,∠CKG=90°,
∴KE=KF﹣EF=2m,
∴GK=GE﹣KE=m,
∵∠G=45°,
∴CK=GK=m,
∴CE2=CK2+KE2=m2+(2m)2=5m2,
∴S1=CD•CE=CE2=,
∵AC=BC=3m,
∴S2=AC•BC=,
∴=;
当D在射线BA上时,延长EG交AC于T,如图:
同理可得BC=AC=EG=3m,
∴FG=EG﹣EF=2m,
∵TF=BC=3m,
∴TG=TF﹣FG=m,
∵∠ACB=90°,CA=CB,O为AB的中点,
∴∠AOC=45°,
∵BC∥EF,
∴∠ETC=90°,
∴CT=TG=m,
∴CE2=CT2+TE2=m2+(m+3m)2=17m2,
∴S1=,
∴=;
综上所述,的值为或.
六.解直角三角形的应用-坡度坡角问题(共1小题)
10.(2023•辽宁)暑假期间,小明与小亮相约到某旅游风景区登山.需要登顶600m高的山峰,由山底A处先步行300m到达B处,再由B处乘坐登山缆车到达山顶D处.已知点A,B,D,E,F在同一平面内,山坡AB的坡角为30°,缆车行驶路线BD与水平面的夹角为53°(换乘登山缆车的时间忽略不计).
(1)求登山缆车上升的高度DE;
(2)若步行速度为30m/min,登山缆车的速度为60m/min,求从山底A处到达山顶D处大约需要多少分钟(结果精确到0.1min).
(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
【答案】(1)450m;
(2)19.4min.
【解答】解:(1)如图,过点B作BM⊥AF于点M,由题意可知,∠A=30°,∠DBE=53°,DF=600m,AB=300m,
在Rt△ABM中,∠A=30°,AB=300m,
∴BM=AB=150m=EF,
∴DE=DF﹣EF=600﹣150=450(m),
答:登山缆车上升的高度DE为450m;
(2)在Rt△BDE中,∠DBE=53°,DE=450m,
∴BD=
≈
=562.5(m),
∴需要的时间t=t步行+t缆车
=+
≈19.4(min),
答:从山底A处到达山顶D处大约需要19.4分钟.
七.列表法与树状图法(共2小题)
11.(2023•辽宁)6月5日是世界环境日,为提高学生的环保意识,某校举行了环保知识竞赛,从全校学生的成绩中随机抽取了部分学生的成绩进行分析,把结果划分为4个等级:A(优秀);B(良好);C(中);D(合格).并将统计结果绘制成如图两幅统计图.
请根据统计图提供的信息,解答下列问题:
(1)本次抽样调查的学生共有 60 名;
(2)补全条形统计图;
(3)该校共有1200名学生,请你估计本次竞赛获得B等级的学生有多少名?
(4)在这次竞赛中,九年一班共有4人获得了优秀,4人中有两名男同学,两名女同学,班主任决定从这4人中随机选出2人在班级为其他同学做培训,请你用列表法或画树状图法,求所选2人恰好是一男一女的概率.
【答案】(1)60;
(2)见解答;
(3)480名;
(4).
【解答】(1)调查的学生共有==60(名);
故答案为:60;
(2)C合格的人数=60﹣24﹣18﹣3=15(名),
(3)1200×=480(名),
答:估计本次竞赛获得B等级的学生有480名;
(4)画树状图如下:
∴一共有12中等可能的情况,其中一男一女的情况有8种,
∴所选2人恰好是一男一女的概率为=.
12.(2021•辽宁)为迎接建党100周年,某校组织学生开展了党史知识竞赛活动.竞赛项目有:A.回顾重要事件;B.列举革命先烈;C.讲述英雄故事;D.歌颂时代精神.学校要求学生全员参加且每人只能参加一项,为了解学生参加竞赛情况,随机调查了部分学生,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)本次被调查的学生共有 60 名;
(2)在扇形统计图中“B项目”所对应的扇形圆心角的度数为 90° ,并把条形统计图补充完整;
(3)从本次被调查的小华、小光、小艳、小萍这四名学生中,随机抽出2名同学去做宣讲员,请用列表或画树状图的方法求出恰好小华和小艳被抽中的概率.
【答案】(1)60;
(2)90°,15人,补图见解答;
(3).
【解答】解:(1)本次被调查的学生共有:9÷15%=60(名);
(2)B项目的人数有:60﹣9﹣12﹣24=15(人),
图中“B项目”所对应的扇形圆心角的度数为:360°×=90°;
补全统计图如下:
(3)根据题意列表如下:
小华
小光
小艳
小萍
小华
(小光,小华)
(小艳,小华)
(小萍,小华)
小光
(小华,小光)
(小艳,小光)
(小萍,小光)
小艳
(小华,小艳)
(小光,小艳)
(小萍,小艳)
小萍
(小华,小萍)
(小光,小萍)
(小艳,小萍)
由表格可以看出,所有可能出现的结果有12种,并且它们出现的可能性相等,其中恰好小华和小艳被抽中的情况有2种.
则恰好小华和小艳被抽中的概率是=.
辽宁省盘锦市2021-2023三年中考数学真题分类汇编-03解答题(提升题)知识点分类: 这是一份辽宁省盘锦市2021-2023三年中考数学真题分类汇编-03解答题(提升题)知识点分类,共34页。试卷主要包含了,与y轴交于点C等内容,欢迎下载使用。
辽宁省阜新市2021-2023三年中考数学真题分类汇编-03解答题(提升题)知识点分类: 这是一份辽宁省阜新市2021-2023三年中考数学真题分类汇编-03解答题(提升题)知识点分类,共35页。试卷主要包含了,交y轴于点C,,与y轴交于点C,,且AE=CF等内容,欢迎下载使用。
辽宁省抚顺市2021-2023三年中考数学真题分类汇编-03解答题(提升题)知识点分类: 这是一份辽宁省抚顺市2021-2023三年中考数学真题分类汇编-03解答题(提升题)知识点分类,共33页。












