高考数学一轮复习基础知识复习课件第12讲函数y=Asinωx+φ（含解析）

这是一份高考数学一轮复习基础知识复习课件第12讲函数y=Asinωx+φ（含解析），共25页。PPT课件主要包含了考点一，考点二，考点三，考点四，答案C，答案D，答案BC，答案2，答案A等内容，欢迎下载使用。

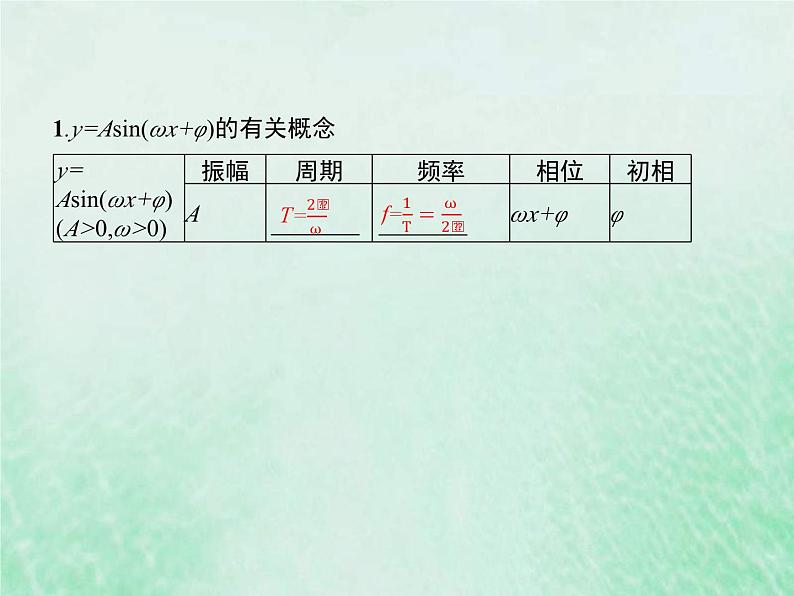
1.y=Asin(ωx+φ)的有关概念
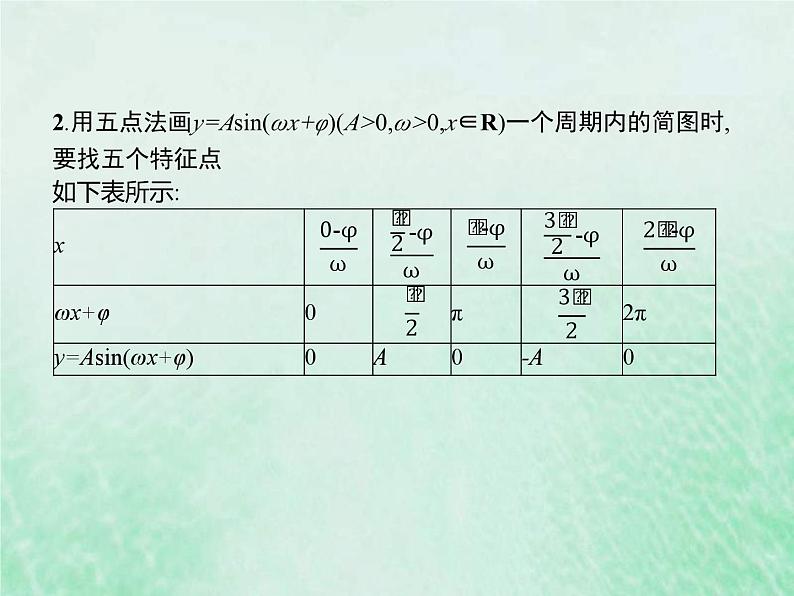
2.用五点法画y=Asin(ωx+φ)(A>0,ω>0,x∈R)一个周期内的简图时,要找五个特征点如下表所示:
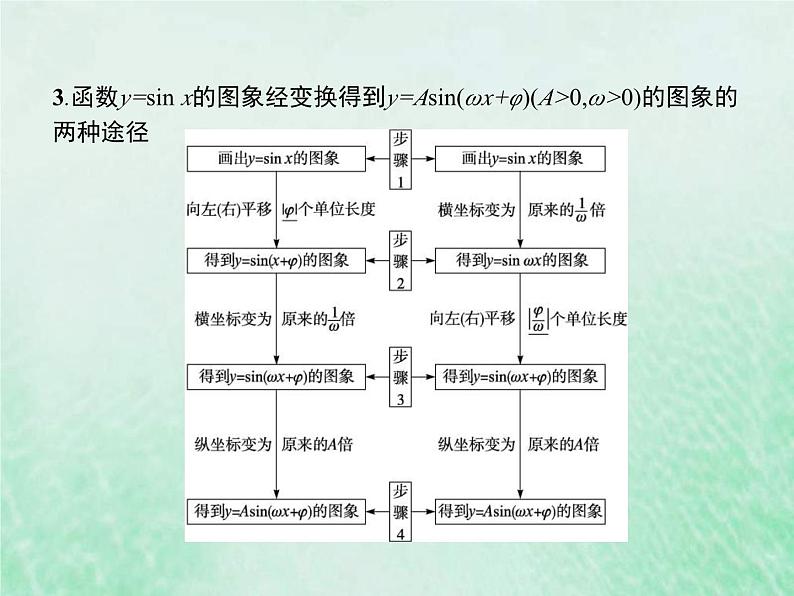
3.函数y=sin x的图象经变换得到y=Asin(ωx+φ)(A>0,ω>0)的图象的两种途径
函数y=Asin(ωx+φ)的图象变换
三角函数图象的变换是高考中的热点.如异名三角函数间的平移变换通常先变成同名函数再平移.一般地,由y=sin x的图象变换成y=Asin(ωx+φ)的图象,两种变换中平移的量的区别:先平移再伸缩,平移的量是|φ|个单位长度;而先伸缩再平移,平移的量是丨 丨个单位长度.特别提醒:平移变换和伸缩变换都是针对x而言.
求函数y=Asin(ωx+φ)的解析式例2(多选)如图是函数y=sin(ωx+φ)的部分图象,则f(x)=(　　)
利用图象求函数y=Asin(ωx+φ)(A>0,ω>0)的解析式主要从以下三个方面考虑:(1)根据最大(小)值,求出A的值;(2)根据最小正周期求出ω的值;(3)求φ的常用方法是把图象上的一个已知点的坐标代入(通常为图象的最高、最低点或零点).
函数y=Asin(ωx+φ)的图象与性质◆角度1.函数周期性例3(2019年6月浙江学考)已知函数f(x)=sin x+sin( -x).(1)求f(0)的值;(2)求函数f(x)的最小正周期;(3)当x∈[0, ]时,求函数f(x)的最小值.
◆角度2.函数的对称性
若x=t时正弦型f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)(余弦型g(x)=Acs(ωx+φ)(A>0,ω>0,|φ|<π))三角函数取得最大值或最小值,则此函数图象的对称轴即为x=t.若x=x0时正弦型(余弦型)三角函数的函数值为0,则点(x0,0)为函数的对称中心.
◆角度3.函数的单调性例5已知函数f(x)=2sin ωxcs ωx+cs 2ωx(ω>0)的最小正周期为π.(1)求ω的值;(2)求f(x)的单调递增区间.
形如f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的函数的单调性问题,一般是将ωx+φ看成一个整体,再结合图象利用y=sin x的单调性求解.如果函数中自变量的系数为负值,要根据诱导公式把自变量系数化为正值,再确定其单调性.
◆角度4.方程根(函数零点)问题
解析 f(x)=4cs2 sin x-2sin x-|ln(x+1)|=2sin x(2cs2 -1)-|ln(x+1)|=sin 2x-|ln(x+1)|,令f(x)=0,得sin 2x=|ln(x+1)|.在同一坐标系中作出两个函数y=sin 2x与函数y=|ln(x+1)|的大致图象如图所示.
观察图象可知,两函数图象有2个交点,故函数f(x)有2个零点.
对于混合函数的零点问题可分解成两个基本初等函数,函数的零点个数问题转化为两个函数图象间的交点个数问题来解决.
求函数y=Asin(ωx+φ)中参数范围问题例7若f(x)=cs x-sin x在[-a,a]是减函数,则a的最大值是(　　)