高考数学一轮复习基础知识复习课件第10讲三角函数的图象与性质（含解析）

这是一份高考数学一轮复习基础知识复习课件第10讲三角函数的图象与性质（含解析），共20页。PPT课件主要包含了考点一，考点二，考点三，考点四，考点五，答案D，答案A等内容，欢迎下载使用。

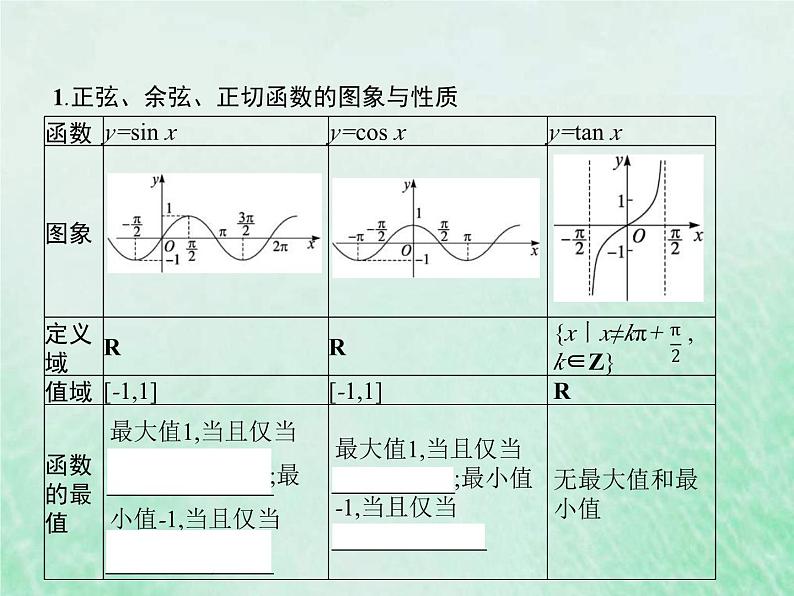
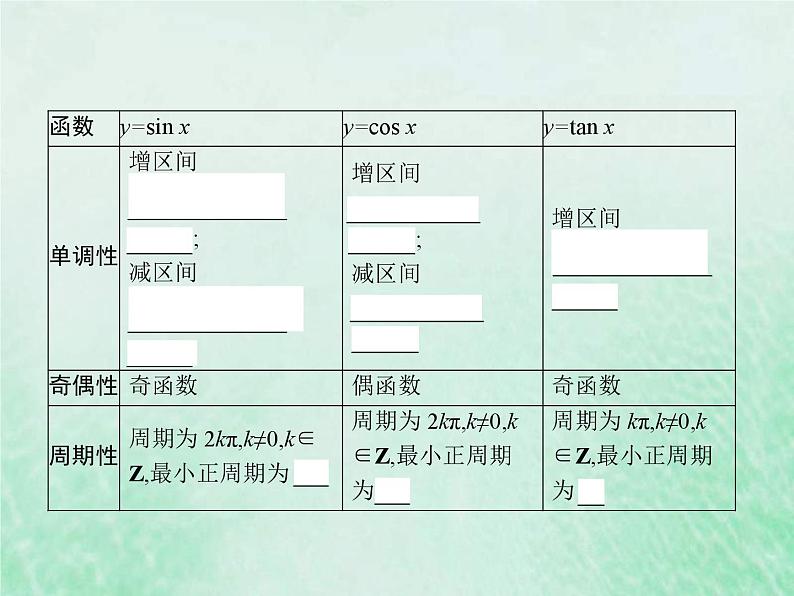
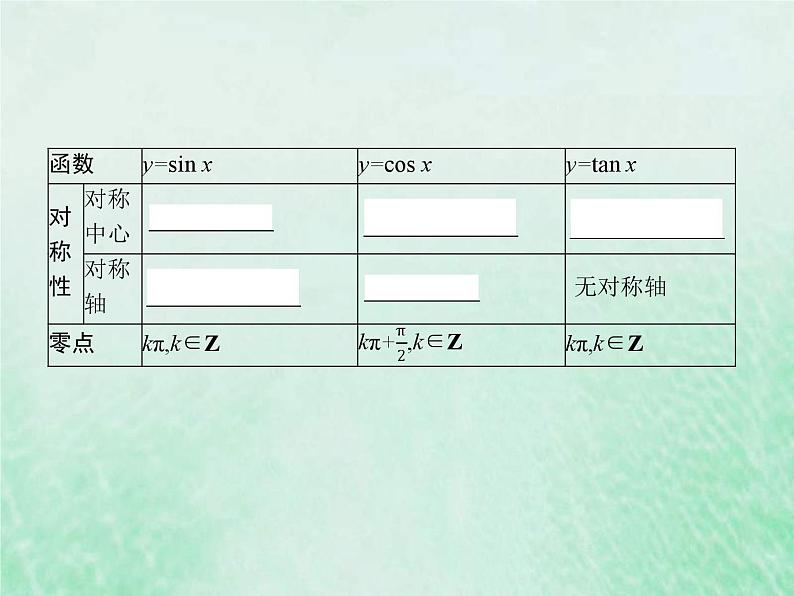
1.正弦、余弦、正切函数的图象与性质
2.周期函数的定义对于函数f(x),如果存在一个非零常数T ,使得当x取定义域内的每一个值时,都有 f(x+T)=f(x),那么函数f(x)就叫作周期函数,非零常数 T叫作这个函数的周期.函数y=Asin(ωx+φ)和y=Acs(ωx+φ)的周期均为
3.对称与周期(1)正弦曲线、余弦曲线相邻的两个对称中心、相邻的两条对称轴之间的距离是半个周期,相邻的对称中心与对称轴之间的距离是四分之一个周期;正切曲线相邻的两个对称中心之间的距离是半个周期.
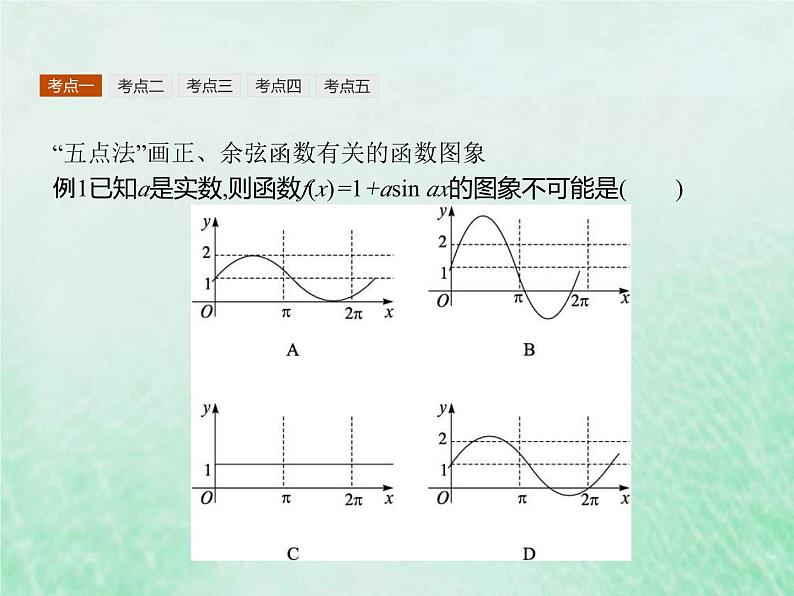
“五点法”画正、余弦函数有关的函数图象例1已知a是实数,则函数f(x)=1+asin ax的图象不可能是(　　)
解析 振幅大于1时,三角函数的周期为T= ,∵|a|>1,∴T<2π,而D不符合要求,故选D.
用“五点法”画函数图象,相位先取 ,再描出对应五点,再用光滑的曲线将描出的五个点连接起来,同时要注意曲线的凹凸性
正、余弦(型)函数的周期性例2(1)下列函数中,最小正周期为π的是(　　)A.y=sin xB.y=cs xC.y=tan xD.y=sin(2)函数y=丨sin 丨的最小正周期是(　　)A.B.πC.2πD.4π
答案 (1)C　(2)C　
解析 (1)y=sin x,y=cs x的周期是2π,y=sin 的周期为4π,y=tan x的周期为π,故选C.(2)函数y=丨sin 丨的图象如下,可观察周期为2π.故选C.
求函数最小正周期的常用方法:(1)公式法;(2)图象法:利用三角函数的图象的特征求最小正周期.如y=|f(x)|型曲线,画出y=f(x)的图象,保留x轴上方的图象,再将x轴下方的图象关于x轴对称翻折到x轴的上方得到y=|f(x)|的图象.
正、余弦(型)函数的对称性
答案 (1)C　(2)A　
解析 (1)∵正弦函数图象的对称轴过图象的最高点或最低点,
对于函数y=Asin(ωx+φ)或y=Acs(ωx+φ)来说,对称中心即为函数图象与x轴的交点.
利用正、余弦(型)函数的奇偶性求参数例4已知a∈R,函数f(x)=sin x-|a|为x∈R上的奇函数,则a等于(　　)A.0B.1C.-1D.±1
解析 方法一　由题意可知,f(x)=-f(-x)得a=0.方法二　函数的定义域为R,又f(x)为奇函数,故其图象必过原点,即f(0)=0,得a=0.
利用函数的奇偶性求参数,根据f(x)±f(-x)=0得到a的等式;或由奇函数图象必过原点,即f(0)=0得解.
正、余弦(型)函数单调性的应用