










奥数五年级下册 第3讲:行程问题(四)流水 课件+教案+作业
展开( 五年级 ) 备课教员:*** | ||
第二讲 行程问题(四)流水 | ||
一、教学目标:
| 知识目标 |
度等量的含义,掌握各量间的关系。
|
能力目标 | 初步养成独立思考、自主探究、合作交流的学习方式。 | |
情感目标 | 感受数学的趣味性,从情境中感悟数学的美。 | |
二、教学重点: | 顺水速度、逆水速度、静水速度及水速等数量间的关系,流水行船问题的解题方法 | |
三、教学难点: | 准确理清顺水速度、逆水速度、静水速度及水速等数量间的关系。 | |
四、教学准备: | PPT | |
五、教学过程: 第一课时(50分钟) 一、导入(5分) 【设计意图:让学生了解流水行船问题的概念,从具体情境中掌握,理解并区分什么是顺水速度、逆水速度、静水速度、水流速度等。】 师:同学们,你们观察过水面吗?当一片叶子掉进水里,叶子会漂得越来越远, 而且是顺着一个方向一直飘走,为什么呢? 生:因为水在流动。 师:是的,水自己在流动,是有一定的速度,这是水自己的速度,我们把它叫 做水流速度。记住了吗? 生:记住了。 师:船如果在静止的水中航行,这个时候船航行的速度我们把它叫做静水速度, 也可以叫做船速,明白吗? 生:…… 师:现在老师给你们看一个小动画(点击PPT),这是一艘小船,蓝色部分代表 的是水,从左往右代表顺水的方向。我们先看第一个动画。 (播放PPT) 师:我们看到小船从左往右走,是顺着水流动的方向的,我们叫做顺水航行, 速度叫做顺水速度,船的速度与水的速度是同一个方向,那么顺水速度就 等于静水速度加水流速度。能理解吗? 生:…… 师:那我们再来看另一个动画,(播放PPT)从右往左逆着水流航行,船的行驶 速度会不会变慢? 生:…… 师:所以逆水速度=静水速度-水流速度。那么通过这个公式我们还可以引申出 更多的公式,这就是我们这节课要学习的。 【探究新知,引入新课: 【板书课题:行程问题(四)流水】 | ||
二、探索发现授课(40分) (一)例题1:(10分) 水流速度是每小时10千米。现有一艘船在静水中航行120千米需6小时,顺水航行相同距离需要几小时? 讲解重点:灵活运用公式:顺水速度=静水速度+水流速度。 (请一位学生读题) 师:读完题目后,你能从中找出哪些已知条件? 生:水流速度是每小时10千米。 师:那么还有一个条件是什么? 生:在静水中航行120千米需6小时。 师:那么我们通过这个条件中求出什么? 生:静水速度。 师:怎么求呢? 生:120÷6=20(千米/小时) 师:那么问题是让我们求什么呢? 生:顺水航行相同距离需要几小时。 师:这是让我们求时间。要求时间,需要知道哪两个条件? 生:路程和速度。 师:是的,路程是多少呢? 生:120千米。 师:这个速度是顺水速度还是逆水速度? 生:顺水速度,它说是顺水航行。 师:是的,可是顺水速度是未知的,怎么办呢?根据哪些条件用什么公式求? 生:顺水速度=静水速度+水流速度,已知水流速度为每小时10千米,求出了静 水速度为20千米/小时,代入公式得:20+10=30(千米/小时)。 师:非常好,知道了路程和顺水速度,求时间大家都会求了吧,请同学上黑板 将解题过程板书出来。 板书: 120÷6=20(千米/小时) 20+10=30(千米/小时) 120÷30=4(小时) 答:顺水航行相同距离需要4小时。
练习1:(5分) 水流速度是每小时15千米。现有一艘船在静水中航行280千米需要7小时,逆水航行275千米需要几小时? 分析: 要求逆水行驶的时间,已知路程,需知道逆水速度,根据逆水速度=静水速度-水流速度,然后将数据带入公式求出时间。 板书: 280÷7-15=25(千米/小时) 275÷25=11(小时) 答:逆水航行275千米需要11小时。
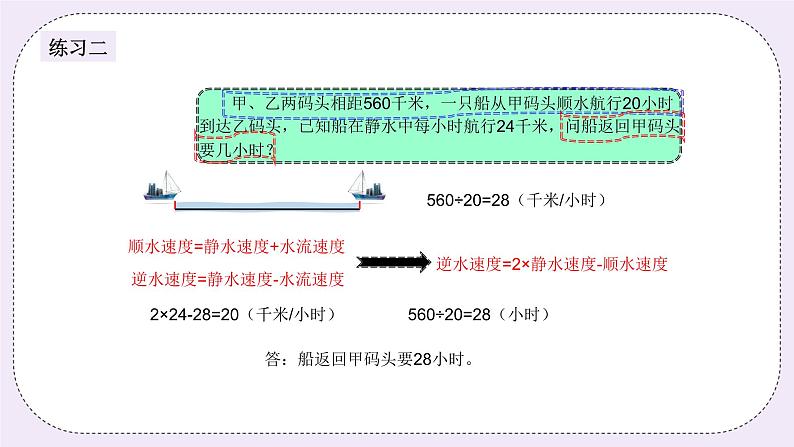
(二)例题2:(10分) 两个码头相距192千米,一艘汽艇顺水行完全程要8小时,已知水流速度是每小时4千米,逆水行完全程要几小时? 讲解重点:灵活地运用公式:逆水速度=顺水速度-2×水流速度,并学会运用它 的变式,在题目中灵活处理题中的条件,使用正确的公式。 师:上一个例题我们是从条件入手的,那这次呢,我们就从问题入手,请同学 们大声告诉我问题是让我们求什么? 生:逆水行完全程要几小时。 师:要求逆水行完全程的时间,需要知道哪些条件? 生:逆水速度和全程。 师:那从题目中能直接找出吗? 生:路程已知,是192千米,逆水速度不知道。 师:那我们可以从哪些条件入手求出逆水速度呢? 生:汽艇顺水行完全程要8小时,已知水流速度是每小时4千米。求出顺水速 度。 师:求出顺水速度之后呢? 生:顺水速度-水流速度=静水速度,静水速度-水流速度=逆水速度。 师:非常棒,我们可以把这两个公式综合一下,即逆水速度=顺水速度-2×水流 速度。 板书: 逆水速度=顺水速度-2×水流速度 能理解吗? 生:…… 师:那么逆水速度我们会求了,那就请大家在自己的草稿本上写下解题过程, 谁来黑板上板书? 生:…… 板书: 192÷8-4×2=16(千米/小时) 192÷16=12(小时) 答:逆水行完全程要12小时。 师:大家一定要记住这个公式,这在流水行船问题中是很重要的公式,也希望 同学们能灵活运用我们学的这几个公式。那么接下来请大家做一做练习。 练习2:(5分) 甲、乙两码头相距560千米,一只船从甲码头顺水航行20小时到达乙码头,已知船在静水中每小时航行24千米,问船返回甲码头要几小时? 分析: 返回甲码头即逆水航行,要求逆水需几小时,先求出逆水速度,由已知条件可得出顺水速度和静水速度,那么逆水速度=2×静水速度-顺水速度。 板书: 560÷20=28(千米/小时) 24×2-28=20(千米/小时) 560÷20=28(小时) 答:船返回甲码头要28小时。 三、小结:(5分) 公式:顺水速度=静水速度+水流速度 逆水速度=静水速度-水流速度 结合具体题目,基于基础公式推导出更多的公式: 逆水速度=顺水速度-2×水流速度 逆水速度=2×静水速度-顺水速度 | ||
第二课时(50分) 一、导入(3分) 【设计意图:让学生通过身边的实际事例,加深理解流水行船问题。】 师:同学们,大家都看了我们这一讲的走进生活了吗? 生:看了。 师:故事中阿派最后赢了欧拉,你们知道这是为什么吗? 生:…… 师:是的,因为阿派是顺水划行的,而欧拉是逆水划行的,所以阿派最后赢了 欧拉。所以我们生活中处处都隐藏着数学知识,学好了数学我们也可以把 它运用到实际生活中去。所以大家一定要认真听。 师:这节课我们继续学习流水行船问题,学会从基本公式中引申出更多的公式 去解决问题。 | ||
二、探索发现授课(42分) (一)例题3:(10分) 某船在静水中每小时行18千米,水流速度是每小时2千米。此船从甲地逆水航行到乙地需要15小时。求甲、乙两地的路程是多少千米?此船从乙地回到甲地需要多少小时? 讲解重点:学会利用流水问题的公式,根据题中的条件提取需要的信息,解出 题目的问题。 (请一位同学来读题) 师:这道题有两个问题需要我们去解,我们先来看第一个问题,求甲、乙两地 的路程,求路程需要知道哪两个条件? 生:速度和时间。 师:那么我们就从题目中来找有用的信息。首先我们来找时间。从哪个条件里 可以找到时间呢? 生:此船从甲地逆水航行到乙地需要15小时。 师:没错,这是逆水的时间,那我们就要找和它有关的逆水速度,逆水速度该 从哪找呢? 生:某船在静水中每小时行18千米,水流速度是每小时2千米。 师:是的,这里已知静水速度和水流速度,那么逆水速度是多少呢? 生:18-2=16(千米/小时) 师:很棒,那么我们就能求出甲、乙之间的路程了,16×15=240(千米)。 师:第一个问题求出来了,我们再来看第二个问题,是让我们求从乙地到甲地 需要的时间。从乙地到甲地是顺水还是逆水? 生:顺水,因为从甲地到乙地是逆水,反过来就是顺水。 师:真聪明。要求顺水行驶的时间,应该怎么求? 生:用路程除以速度。 师:没错,路程我们已经求出来,那么速度呢? 生:顺水速度=静水速度+水流速度。18+2=20(千米/小时) 师:非常好,那么我们就可以用240÷20=12(小时),求出顺水航行的时间。 板书: 15×(18-2)=240(千米) 240÷(18+2)=12(小时) 答:甲、乙两地的路程是240千米。此船从乙地回到甲地需要12小时。 练习3:(5分) 已知一条河的水流速度是每小时6千米,一艘船在静水中3小时航行48千米。这艘船从甲地顺水航行到乙地需要10小时。求甲、乙两地的路程是多少千米?此船从乙地回到甲地需要几小时? 分析: 要求甲、乙两地的路程,从甲地到乙地是顺水航行,那么就要找出顺水速度和顺水航行的时间;从乙地到甲地是逆水,要求逆水航行的时间,就要先找出逆水速度和总路程。 板书: 48÷3=16(千米/小时) (16+6)×10=220(千米) 220÷(16-6)=22(小时) 答:甲、乙两地的路程是220千米。此船从乙地回到甲地需要22小时。
(二)例题4:(12分) 一艘轮船往返于AB两地之间,由A到B顺水航行,由B到A逆水航行。已知船在静水中的速度为每小时25千米,由A到B用了6小时,由B到A用的时间是A到B所用时间的1.5倍,求水流速度。 讲解重点:当顺水速度、逆水速度及具体的时间是未知的时候,会灵活地运用 公式:顺水速度=静水速度+水流速度,逆水速度=静水速度-水流速 度,推出:静水速度=(顺水速度+逆水速度)÷2,进而解决问题。 (学生读题) 师:读完题后,你找出了哪些已知条件? 生:静水速度是每小时25千米;由A到B用了6小时,由B到A用的时间是A 到B所用时间的1.5倍。 师:嗯,很好,那问题是让我们求什么呢? 生:水流速度。 师:根据我们的已知条件能求出水流速度吗? 生:…… 师:我们换一个角度考虑,同一段路程逆水航行的时间是顺水航行时间的1.5 倍,那么顺水航行的速度是逆水速度的1.5倍,能理解吗? 生:…… 师:我们将逆水速度看做1倍数,那么顺水速度是几倍呢? 生:1.5倍。 师:很好。我们知道静水速度=(顺水速度+逆水速度)÷2,那么静水速度就是 (1倍+1.5倍)÷2=1.25倍,即静水速度是逆水速度的1.25倍,那么逆水 速度是多少呢? 生:25÷1.25=20(千米/小时) 师:水流速度呢? 生:25-20=5(千米/小时) 板书: (1倍+1.5倍)÷2=1.25倍 25÷1.25=20(千米/小时) 25-20=5(千米/小时) 答:水流速度是每小时5千米。 师:同学们在遇到类似问题的时候,要学会灵活运用我们所学的公式,这些基 础的公式是可以推出很多的新公式的。接下来同学们自己做一做练习4。
练习4:(5分) 某船在静水中的速度是每小时20千米,水流速度是每小时2千米,该船先顺流而下,后逆流而上返回出发地,共航行6小时,该船最多行了多远? 分析: 要求路程,就得先找到速度和时间。船从起点出发又原路回到起点,逆水航行和顺水航行的路程是相同的。求出顺水速度和逆水速度,知道顺水速度是逆水速度的几倍,那么逆水时间就是顺水时间的几倍,然后求出时间,最后根据公式求出路程。 板书: 解:设顺水行驶时间为9a小时, 20+2=22(千米/小时) 20-2=18(千米/小时) 逆水时间为22×9a÷18=11a(小时), 11a+9a=6 a=0.3 0.3×11×18=59.4(千米) 答:该船最多行了59.4千米远。 例题5:(选讲) 有甲、乙两船,甲船和漂流物同时由上游A处顺江而下,乙船也同时从下游B处沿江而上。甲船行4小时后与漂流物相距100千米,乙船行12小时后与漂流物相遇,两船的划速相同。问A、B间的距离是多少千米? 讲解重点:了解漂流物与船相对运动时,是相遇问题,他们的速度和=静水速度。 理解漂流物与船同向运动时,他们的速度差是静水速度。 (学生读题) 师:甲船从上游顺江而下,乙船同时从下游顺江而上,那么甲乙两船是不是我 们行程问题的相遇问题? 生:是。 师:有一漂流物与甲同时顺流而下,你们知道漂流物的速度与什么速度是相同 的吗? 生:…… 师:漂流物自己有速度吗? 生:没有。 师:那么它是靠什么顺流而下呢? 生:…… 师:所以它的速度就是水流速度。乙船的速度是逆水速度,相遇问题是怎么求 路程的? 生:速度和×相遇时间=路程 师:很好,我们来看速度和,速度和就是水流速度+乙船的逆水速度,逆水速度 =静水速度-水流速度,综合一下就是速度和=水流速度+(静水速度-水流速 度)=静水速度。已知相遇时间,我们只需求出速度和即静水速度。 师:我们还有一个条件没看,甲船行4小时后与漂流物相距100千米,从这个 条件中我们可以得出什么信息?同学们自己画图、利用公式想想。 生:…… 师:甲船与漂流物都是顺流而下的,漂流物的速度就是水流速度,甲船的顺水 速度=水流速度+静水速度,甲船的顺水速度与漂流物的水流速度相差的就 是一个静水速度,由此,我们可以根据路程差和时间求出他们的速度差即 静水速度为100÷4=25(千米/小时)。 师:知道了静水速度和相遇时间,A、B间的距离是25×12=300(千米) 板书: 100÷4=25(千米/小时) 25×12=300(千米) 答:A、B间的距离是300千米。
练习5:(选做) 有两只木排,甲木排和漂流物同时由上游A地向下游B地前行,乙木排也同时从B地向A地前行,甲木排5小时后与漂流物相距75千米,乙木排行15小时后与漂流物相遇,两木排的划速相同,A、B两地相距多少千米? 分析: 甲木排与漂流物之间的速度差是静水速度,乙木排与漂流物是相向运动,速度和是静水速度,速度和×相遇时间=路程。 板书: 75÷5×15=225(千米) 答:A、B两地相距225千米。
三、总结:(5分) 顺水速度=静水速度+水流速度 逆水速度=静水速度-水流速度 静水速度(船速)=(顺水速度+逆水速度)÷2 水速=(顺水速度-逆水速度)÷2
四、随堂练习:
水少行9千米,逆水比顺水多用几小时? 板书: 432÷(432÷16-9)-16=8(小时) 答:逆水比顺水多用8小时。
时,船速和水速分别是多少? 板书: 120÷10=12(千米/小时) 120÷6=20(千米/小时) 船速:(12+20)÷2=16(千米/小时) 水速:(20-12)÷2=4(千米/小时) 答:船速是16千米每小时,水速是4千米每小时。
3. 80千米的水路,已知甲船顺流而下需要4小时,逆流而上需要10小时。如 果乙船顺流而下需5小时,问乙船逆流而上需要几小时? 板书: 水速:(80÷4-80÷10)÷2=6(千米/小时) 乙船逆水速度:80÷5-6×2=4(千米/小时) 80÷4=20(小时) 答:乙船逆流而上需要20小时。
船在静水中的速度为每小时36千米,求A、B两地之间的距离。 板书: 顺水速度=(7÷5)倍的逆水速度 (顺水速度+逆水速度)÷2=36(千米/小时) 逆水速度=72÷(1+1.4)=30(千米/小时) 30×7=210(千米) 答:A、B两地之间的距离是210千米。
并调转船头时,帽子与船已经相距4千米。已知小船的静水速度为每小时8 千米,水流速度是每小时4千米,那么卡尔需要多少时间追上帽子? 板书: 4÷(8+4-4)=0.5(小时) 答:卡尔需要0.5小时追上帽子。
| ||
家庭作业 |
| |
主管评价 |
| |
主管评分 |
| |
课后反思 (不少于60字) | 整体效果 |
|
设计不足之处 |
| |
设计优秀之处 |
| |
奥数四年级下册 第3讲:追及问题 课件+教案+作业: 这是一份奥数四年级下册 第3讲:追及问题 课件+教案+作业,文件包含奥数四年级下册第3讲追及问题课件pptx、奥数四年级下册第3讲追及问题教案doc、奥数四年级下册第3讲追及问题作业docx等3份课件配套教学资源,其中PPT共15页, 欢迎下载使用。
奥数五年级上册寒假课程第5讲《行程问题》课件+教案: 这是一份奥数五年级上册寒假课程第5讲《行程问题》课件+教案,文件包含奥数五年级上册寒假课程第5讲《行程问题》课件ppt、奥数五年级上册寒假课程第5讲《行程问题》教案doc等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
【奥数】四年级下册数学奥数课件-第11讲《分段计算的行程问题》 全国通用: 这是一份【奥数】四年级下册数学奥数课件-第11讲《分段计算的行程问题》 全国通用,共20页。PPT课件主要包含了知识精讲,极限挑战,例题讲解,巩固提升,数学知识点等内容,欢迎下载使用。













