奥数五年级上册寒假课程第5讲《行程问题》课件+教案

星座站                                                  备课教员：***

                      第五讲   行程问题

一、教学目标：

1、能通过画线段图或实际演示，理解什么是“同时出发”、“相向而行”、“相遇”等术语，形成空间表象。

2、掌握两个物体运动中，速度、时间、路程之间的数量关系，会根据此数量关系解答求路程的相遇应用题。能用不同方法解答相遇求路程的应用题，培养学生的求异思维能力。

3、通过阐明数学在日常生活的广泛应用，激发学生学习数学的兴趣。

二、教学重点：

掌握相遇问题的结构特点，弄懂每经过一个单位时间两物体的变化，并能根据速度、时间、路程的数量关系解相遇求路程的应用题。

三、教学难点：

理解行程问题中的“相遇求路程”的解题思路

四、教学准备：

PPT

五、教学过程：

第一课时（40分钟）

一、外星游记（5分钟）

师：老师遇到了困难,需要同学们帮忙,你们要不要帮忙?

生：要。

师：今天我和妈妈打赌,晚上回家我要和她同时到家，但是我妈妈比我下班早。

生：那老师可以走得比老师妈妈快点。

师：那要快多少呢，我妈妈平时一分钟能走40米，她的公司到家里有1000米,而且她是5点钟下班的,我到家的距离是810米,我是5点10分下班。

生：不知道。

师：那你们想到了再告诉我好不好？

生：好。

师：今天我们学习的课题与我这个问题有关。

【出示课题：行程问题】

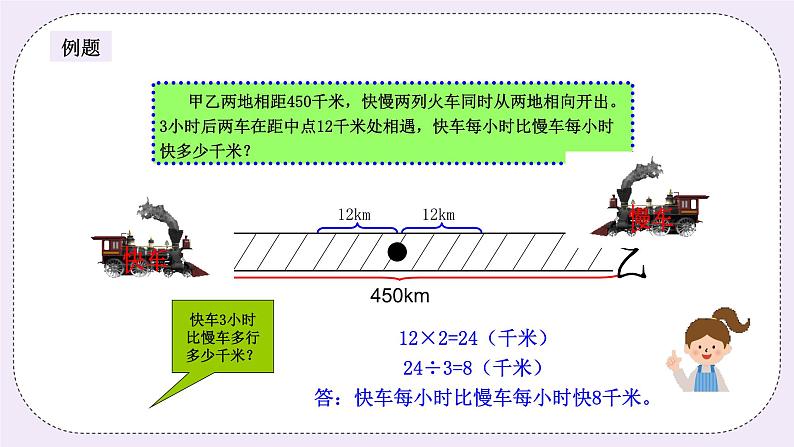
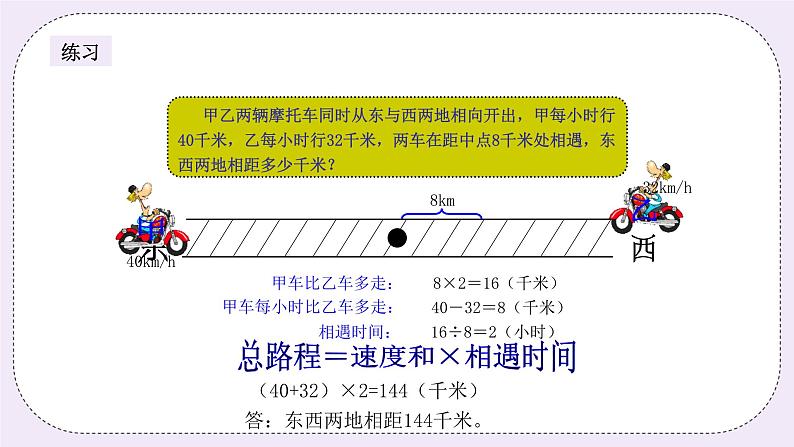
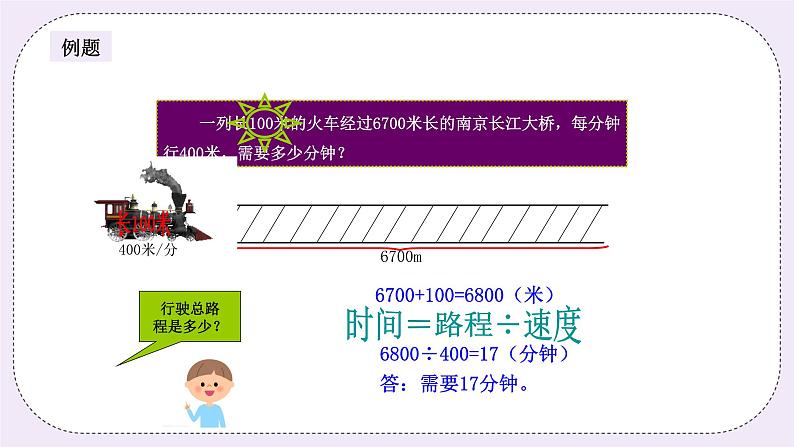
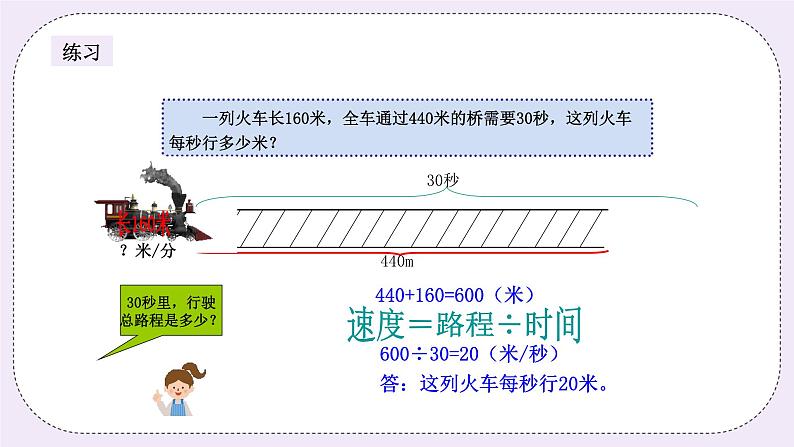
二、星海遨游（30分钟）

（一）星海遨游1（10分钟）

    甲、乙两地相距450千米，快慢两列火车同时从两地相向开出。3小时后两车在距中点12千米处相遇，快车每小时比慢车每小时快多少千米？

师：快车和慢车同时从两地相向开出，3小时后两车距中点12千米处相遇，哪辆车行得更多？

生：快车。

师：快车多行了多少呢？

生：多行了12×2=24（千米）

师：这里要计算快车每小时比慢车每小时快多少千米,那我们是不是只要用快车比慢车多行的距离除以时间就能算出了?

生：是。

板书：

    12×2=24（千米） 

    24÷3=8（千米） 

答：快车每小时比慢车每小时快8千米。

（一）星海历练1（5分钟）

   甲乙两辆摩托车同时从东与西两地相向开出，甲每小时行40千米，乙每小时行32千米，两车在距中点8千米处相遇，东西两地相距多少千米？

分析：

    甲乙两车同时从两地相向开出，两车在距中点8千米处相遇。甲车比乙车多走8×2=16（千米）,甲车每小时比乙车多走：40－32＝8（千米）,这样就可以求出两车相遇的时间为：16÷8＝2（小时），进而求出东西两地总路程:（40+32）×2=144（千米）

板书：

    甲车比乙车多走：8×2＝16（千米）

    甲车每小时比乙车多走：40－32＝8（千米）

    相遇时间：16÷8＝2（小时）

    总路程=速度和×相遇时间

   （40+32）×2=144（千米）

答：东西两地相距144千米。

（二）星海遨游2（10分钟）    

    一列长100米的火车经过6700米长的南京长江大桥，每分钟行400米，需要多少分钟？

师：要求时间，时间计算公式是什么？

生：路程÷速度=时间

师：恩，那我们这一题怎么做呢，是不是用南京长江大桥的长度除以速度啊？

生：不是。

师：那是什么？

生：因为火车也有长度，不能忽略。

师：是的，同学们你们太聪明了，因为火车是通过桥的，所以还要加上车的长度，这才是总路程。

板书:

    行驶路程：6700+100=6800（米）

    行驶时间：6800÷400=17（分钟）

答：需要17分钟。

（二）星海历练2（5分钟）  

   一列火车长160米，全车通过440米的桥需要30秒，这列火车每秒行多少米？

分析：

    火车经过桥的行驶路程：桥长+车长=440+160=600（米），根据公式：路程÷速度=时间。

       160米        440米

板书：

    行驶路程：440+160=600（米）

    行驶速度：600÷30=20（米/秒）

答：这列火车每秒行20米。

三、火星漫步（5分钟）

    “火车过桥”问题也是行程问题的一种情况，同样涉及到路程、速度与时间之间的数量关系。但是，火车是运动的，桥是静止的，火车通过大桥是指车头上桥到车尾离桥，而火车有一定的长度不能忽略不计，即火车过桥的路程就是车身长和桥长之和。根据路程÷时间=速度，可以求出火车每秒行多少米。

                          第二课时（50分钟）

一、外星游记（5分钟）

师：同学们，老师的问题能解决了吗？

生：能。

师：那么谁来帮我算一算？

生：（举手回答）每小时走54米。

师：同学们，他答对了吗？

生：对了。

师：真的吗？到时候如果我打赌输了，那下次上课我要找你们麻烦的哦。

师：接下来我们继续回到课堂。

（出示PPT）

二、太空遨游（30分钟）

（一）太空遨游1（10分钟）

    甲、乙两地间的路程是600千米，上午8点客车以平均每小时60千米的速度从甲地开往乙地。货车以平均每小时50千米的速度从乙地开往甲地。要使两车在全程的中点相遇,货车必须在上午几点出发？

师：货车是以平均每小时50千米的速度行驶,而客车是平均每小时60千米前进,同学们,要使两车在中点相遇,应该哪一辆车先出发?

生：货车。

师：两车在中点相遇,那么你们知道客车和火车各行多少千米吗?

生：300千米。

师：那么货车和客车各行驶了多少小时也就能算出来了，用路程除以各自的速度是不是？

生：是。

师：货车和客车的行驶时间是多少？

生：客车行驶时间为300÷60=5(小时)。                                

生：货车的时间300÷50=6(小时)。

师：客车是上午8点出发的，那么，货车需要什么时候出发？

生：上午7点，提前一个小时。

师：是的，同学们，都很聪明。

板书:

    600÷2=300（千米）

    客车行驶时间：300÷60=5（小时）

    货车行驶时间：300÷50=6（小时）

    相差的时间：6-5=1（小时）

答：货车必须在上午7点出发。

（一）太空探险1(5分钟)

    A、B两地相距352千米。甲、乙两汽车从A、B两地对开。甲车每小时行36千米，乙车每小时行44千米。乙车因事，在甲车开出32千米后才出发。两车从各自出发起到相遇时，哪辆汽车走的路程多？多多少千米？

分析:

    根据题目条件,可以求出相遇时间=总路程÷速度和：（352－32）÷（44+36）=4（小时），在这期间，乙车所行距离：44×4=176（千米），甲车所行距离：36×4+32=176（千米），所以两车所行路程相等。

板书：

    相遇时间：（352－32）÷（44+36）=4（小时）

    甲车所行距离：36×4+32=176（千米）

    乙车所行距离：44×4=176（千米）

答：两辆汽车走的路程相等。

（二）太空遨游2（10分钟）

    甲、乙两站相距360千米。客车和货车同时从甲站出发驶向乙站，客车每小时行60千米，货车每小时行40千米，客车到达乙站后停留0.5小时，又以原速返回甲站，两车相遇的地点离乙站多少千米？

师：客车和货车同时从甲站出发,客车到达乙站之后,停留了0.5小时，这个过程货车在做什么呢？

生：货车一直在行驶。

师：那这个过程花了多少时间，同学们能计算出来吗？

生：先算出客车从甲站到达乙站的时间，360÷60=6(小时),在加上休息的的0.5个小时,总共花了6.5个小时。

师：嗯，对了，这样我们就可以算出这段时间货车行驶了多少，怎么计算？

生：货车行驶了40×(6+0.5)=260(千米)。

师：这时货车和客车相距多少千米？

生：用总路程减去货车行驶的路程。

师：是的，同学们都非常聪明，这个问题就可以转化为相遇问题了是不是?

生：是。

师：用路程除以速度和就能算出相遇时间，就可以求出相遇地点离乙站的距离。

师：这是常规的解题思路，这道题还有另外一种计算方法，我们可以假设客车到了乙站后不休息，而是继续行驶0.25小时，再返回,此时我们可以计算出两车所行驶的路程和，360×2+60×0.5=750(千米),进而算出相遇时间，同样的，就能算出相遇时货车行驶的路程,再用总路程减去货车行驶的路程，就可以得到答案了。

板书:

方法一：客车从甲站行至乙站需要：360÷60=6(小时)

        客车在乙站停留0.5小时后开始返回甲站时，货车行了：

            40×(6+0.5)=260(千米)

        货车此时距乙站还有：

            360-260=100(千米)

        货车继续前行,客车返回甲站(化为相遇问题)“相遇时间”为：

            100÷(60+40)=1(小时)

      所以，相遇点离乙站60×1=60(千米)

方法二：

    假设客车到达乙站后不停,而是继续向前行驶(0.5÷2)=0.25小时后返回，     那么两车行驶路程之和为：360×2+60×0.5=750(千米)

     两车相遇时货车行驶的时间为：750÷(40+60)=7.5(小时)

     所以两车相遇时货车的行程为：40×7.5=300(千米)

     故两车相遇的地点离乙站：360-300=60(千米)

答：两车相遇的地点离乙站60千米。

（二）太空探险2（5分钟）

    甲、乙两地相距47.5千米，哥哥由甲地出发走向乙地，每小时走6.5千米，2小时后，弟弟从乙地走向甲地，弟弟走3小时遇见哥哥，弟弟每小时走多少千米？

分析:

    哥哥和弟弟相遇时,哥哥总共走了:6.5×(2+3)=32.5(千米),那么弟弟总共走的路程:47.5-32.5=15(千米),弟弟每小时走的路程:15÷3=5（千米）。

板书：

    两小时后哥哥走的路程：6.5×2=13（千米）

    相遇时弟弟走的路程：47.5-13-6.5×3=15（千米）

    弟弟每小时走的路程：15÷3=5（千米/小时）

答：弟弟每小时走5千米。

三、火星漫步（5分钟）

    相遇问题是指两个人或车辆（物体……）各按着一定的速度从两地同时出发，沿着同一条道路相向而行（有时相背而行也可看做相遇问题），并由各种条件的变化而产生的一类应用题。

基本数量关系式是：

    速度和×相遇时间=相遇路程

    相遇路程÷相遇时间=速度和

    相遇路程÷速度和=相遇时间

四、决战太空城（见PPT）

家庭作业：

主管评分

课后反思

（不少于60字）