《回顾与思考探究图形变化之旋转》导学案-八年级下册数学北师大版

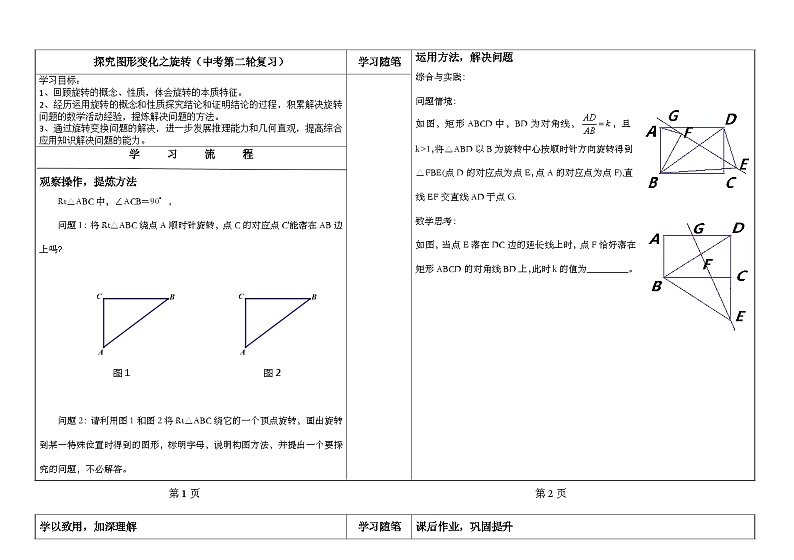
探究图形变化之旋转（中考第二轮复习）

学习随笔

运用方法，解决问题

综合与实践：

问题情境：

如图，矩形ABCD中，BD为对角线，，且k>1，将△ABD以B为旋转中心按顺时针方向旋转得到△FBE(点D的对应点为点E，点A的对应点为点F),直线EF交直线AD于点G.

数学思考：

如图，当点E落在DC边的延长线上时，点F恰好落在矩形ABCD的对角线BD上，此时k的值为_________。

学习目标： 

1、回顾旋转的概念、性质，体会旋转的本质特征。

2、经历运用旋转的概念和性质探究结论和证明结论的过程，积累解决旋转问题的数学活动经验，提炼解决问题的方法。

3、通过旋转变换问题的解决，进一步发展推理能力和几何直观，提高综合应用知识解决问题的能力。

学     习     流     程

观察操作，提炼方法

Rt△ABC中，∠ACB＝90°，

问题1：将Rt△ABC绕点A顺时针旋转，点C的对应点C'能落在AB边上吗？

                图1                             图2

问题2：请利用图1和图2将Rt△ABC绕它的一个顶点旋转，画出旋转到某一特殊位置时得到的图形，标明字母，说明构图方法，并提出一个要探究的问题，不必解答。

学以致用，加深理解

当AD=4，AB=3时，在△ABD绕点B旋转的过程中，利用下图探究问题：

（1）    当AB的对应边FB与AB垂直时,直接写出的值。

（2）当AB的对应边FB在直线BD上时，请画出图形并写出的值。

学习随笔

课后作业，巩固提升

如图1，△ABC和△AED都是等腰直角三角形，∠BAC=∠EAD=90°，点B在线段AE上，点C在线段AD上。

（1）请直接写出线段BE与线段CD的关系：           ；

（2）如图2，将图1中的△ABC绕点A顺时针旋转角α（0＜α＜360°），

①（1）中的结论是否成立？若成立，请利用图2证明；若不成立，请说明理由；

②当AC=ED时，探究在△ABC旋转的过程中，是否存在这样的角α，使以A、B、C、D四点为顶点的四边形是平行四边形？若存在，请直接写出角α的度数；若不存在，请说明理由。