数学八年级上册1 等腰三角形的性质图片ppt课件

这是一份数学八年级上册1 等腰三角形的性质图片ppt课件，共23页。PPT课件主要包含了北京五塔寺，西安半坡博物馆，斜拉桥梁，埃及金字塔，相等的两条边叫做腰，另一条边叫做底边，两腰所夹的角叫做顶角，并剪去绿色部分，ABAC，等腰三角形等内容，欢迎下载使用。

§13.3.1等腰三角形性质的探究
图中有哪些你熟悉的图形
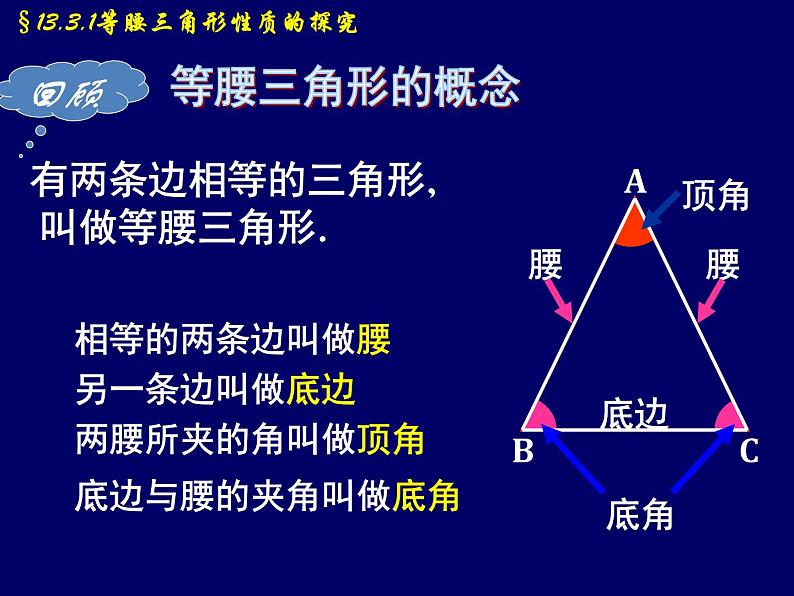
有两条边相等的三角形, 叫做等腰三角形.
等腰三角形的概念
底边与腰的夹角叫做底角
学习目标：1.经历剪纸、折纸等活动，进一步认识等腰三角形， 了解等腰三角形是轴对称图形. 2.能够探索、归纳、验证等腰三角形的性质，并学会运用等腰三角形的性质．3.学习分类讨论思想，提高添加辅助线解决问题的能力．学习重点： 探索并证明等腰三角形性质．
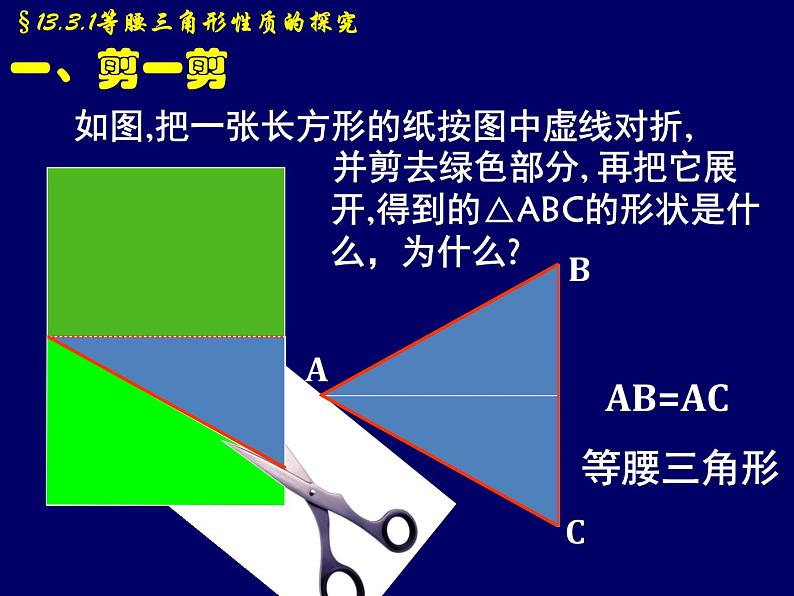
如图,把一张长方形的纸按图中虚线对折,
再把它展开,得到的△ABC的形状是什么，为什么?
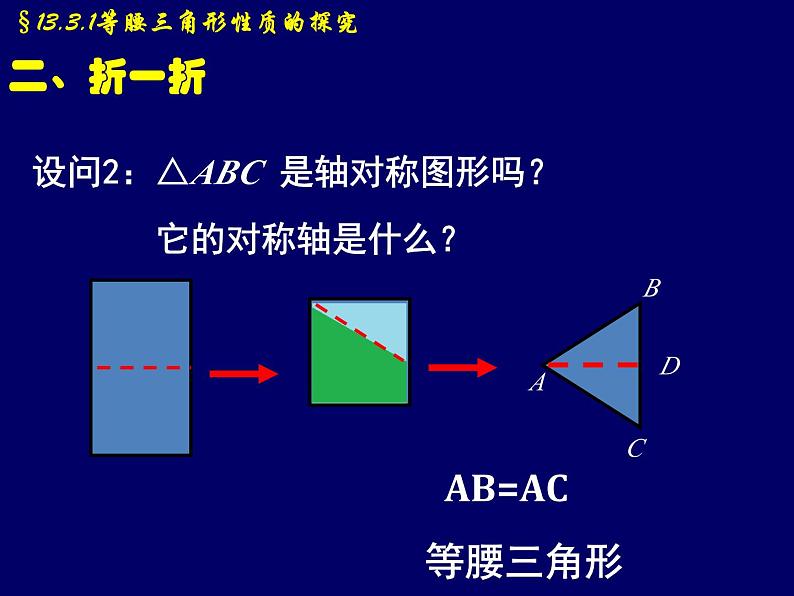
设问2：△ABC 是轴对称图形吗？ 它的对称轴是什么？
相等的线段：AB＝AC　　AD＝ADBD＝CD
相等的角：∠ADB＝∠ADC∠ BAD＝ ∠ CAD ∠B＝∠C
→ AD为底边BC上的中线
→ AD为顶角∠ BAC的平分线
→ AD为底边BC上的高
设问3：你还能发现剪出的等腰三角形角与边具有哪些特征吗？
继续猜想等腰三角形ABC有哪些特性？
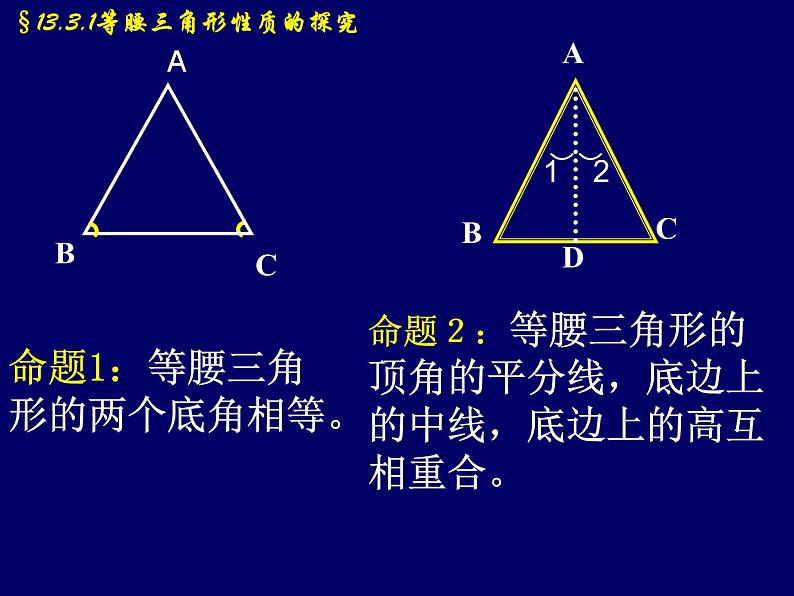
命题1：等腰三角形的两个底角相等。
命题２：等腰三角形的顶角的平分线，底边上的中线，底边上的高互相重合。
证法一:作底边的中线AD
证法二:作底边的高AD
证法三:作顶角的平分线AD
命题1：等腰三角形的两个底角相等
已知：如图，ABC中 ， AB=AC.求证：  B=C.
已知： 如图，在△ABC中，AB=AC.求证： ∠B= ∠C.
等腰三角形的两个底角相等。
作底边的中线AD，则BD=CD
AB=AC ( 已知 )
BD=CD ( 已作 )
AD=AD (公共边)
∴ △BAD ≌ △CAD (SSS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中
方法一：作底边上的中线
作底边的高线AD，则∠BDA=∠CDA=90°
∴ Rt△BAD ≌ Rt△CAD (HL).
在Rt△BAD和Rt△CAD中
作顶角的平分线AD，则∠1=∠2
∠1=∠2 ( 已作 )
∴ △BAD ≌ △CAD (SAS).
方法三：作顶角的平分线
命题2：等腰三角形的顶角的平分线，底边上的中线， 底边上的高互相重合。
已知：如图，ABC中 ， AB=AC.求证:(1) 若AD平分∠BAC， 则AD为底边 BC的中线，AD⊥BC． (2) 若AD为底边BC的中线， 则AD平分∠BAC，AD⊥BC． (3) 若AD为底边BC的高， 则AD平 分∠BAC，AD为底边BC的中线.
AD平分∠BAC ，则∠BAD=∠CAD
∠BAD=∠CAD( 已证 )
∴ BD= CD, ∠BDA=∠CDA
已知：如图，ABC中 ， AB=AC.求证:(1) 若AD平分∠BAC， 则AD为底边 BC的中线，AD⊥BC．
∴ AD为底边 BC的中线 AD⊥BC
证明： AD为底边BC的中线，则BD=CD
BD=CD ( 已证 )
∴ ∠BAD=∠CAD， ∠BDA=∠CDA
已知：如图，ABC中 ， AB=AC.求证： (2) 若AD为底边BC的中线， 则AD平分∠BAC，AD⊥BC．
∴ AD平分∠BAC AD⊥BC
AD为底边BC的高，则∠BDA=∠CDA=90°
∴ ∠BAD=∠CAD, BD= CD
已知：如图，ABC中 ， AB=AC.求证:(3) 若AD为底边BC的高， 则AD平 分∠BAC，AD为底边BC的中线.
∴ AD平 分∠BAC，AD为底边BC的中线
命题1：等腰三角形的两底角相等。
1.已知等腰三角形的一个底角是70°则其余 两角为______________________；2.已知等腰三角形一个角是70°，则其余两 角为_________________________________；3.已知等腰三角形一个角是110°，则其余两 角为______________________；
70°, 40°或55°, 55°
已知：△ABC中，AB＝AC，D是BC边上的中点，DF⊥AC 于F,DE⊥AB于E 。求证：DE＝DF。
在△DBE与△DCF中 ∠DEB＝∠DFC（已证） ∠B＝∠C（已证） BD＝DC（已证）∴ △BDE ≌ △CDF（AAS）∴DE＝DF
已知：△ABC中，AB＝AC，D是BC边上的中点，DF⊥AC 于FDE ⊥ AB 于E 。求证：DE＝DF。
证明： ∵DE⊥AB，DF⊥AC（已知） ∴∠BED＝∠CFD 又∵D是BC中点（已知） ∴BD＝DC 又∵AB＝AC（已知） ∴∠B＝∠C（等边对等角）
方法二：连AD 。 ∵AB＝AC，BD＝DC（已知） ∴AD是∠BAC的平分线又∵DE⊥AB DF⊥AC ∴DE＝DF（角平分线上的点到这个角的两边距离相等）
（等腰三角形三线合一）
方法三（面积法）：连AD 。 ∵ BD＝DC ∴又∵ ∴又∵ AB＝AC ∴ DE=DF
已知：△ABC中，AB＝AC，D是BC边上的中点，DF⊥AC 于F，DE ⊥ AB 于E 。求证：DE＝DF。