四川省成都实验外国语学校西区2023-2024学年九年级上学期开学数学试卷（含答案）

这是一份四川省成都实验外国语学校西区2023-2024学年九年级上学期开学数学试卷（含答案），共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2023-2024学年四川省成都实验外国语学校西区九年级（上）开学数学试卷
一、选择题（每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）
1．（4分）我国新能源汽车产业发展取得了明显成效，逐渐进入市场化驱动阶段．下列新能源汽车图标中，既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
2．（4分）下列从左到右的变形中，是因式分解的是（　　）
A．3xy2＝3x•y•y B．x2+2x+2＝x（x+2）+2
C．a2﹣4＝（a+2）（a﹣2） D．（x+3）2＝x2+6x+9
3．（4分）下列方程属于一元二次方程的是（　　）
A．x3+1＝x2 B．x2+x﹣1＝0 C．x﹣3＝0 D．
4．（4分）下列一元二次方程中没有实数根的是（　　）
A．x2﹣3x＝0 B．x2+3x﹣1＝0 C．2x2﹣4x+3＝0 D．5x﹣2＝3x2
5．（4分）若把分式中x和y的值都扩大为原来的2倍，则分式的值（　　）
A．扩大为原来的2倍 B．缩小为原来的
C．缩小为原来的 D．扩大为原来的4倍
6．（4分）如图，已知菱形ABCD的周长为4，两条对角线AC、BD的和为6（　　）

A．2 B．3 C．4 D．2
7．（4分）现在5G手机非常流行，5G手机速度很快，比4G下载速度每秒多120MB，5G比4G要快200秒，那么5G手机的下载速度是多少呢？若设5G手机的下载速度为xMB秒（　　）
A． B．
C． D．
8．（4分）设y＝x2+3x﹣5，下表列出了x与y的6对对应值：
x
﹣1
0
1
2
3
4
y
﹣7
﹣5
﹣1
5
13
23
根据表格能够发现一元二次方程x2+3x﹣5＝0的一个解的大致范围是（　　）
A．﹣7＜x＜﹣5 B．﹣1＜x＜0 C．﹣5＜x＜﹣1 D．1＜x＜2
二、填空题（每小题4分，共20分，请将答案填在答题卷对应的横线上）
9．（4分）把6a2b﹣3ab因式分解的结果是 　 　．
10．（4分）若分式的值为0，则x＝　 　．
11．（4分）若关于x的方程x2+2ax+4a＝0有一个根为﹣3，则a的值是 　 　．
12．（4分）成都大运会主火炬塔位于东安湖体育公园，如图，小明想测量东安湖A，他在东安湖的一侧选取一点O，分别取OA，N，但M，N之间被障碍物遮挡，于是小明在AO，BO延长线上分别选取P，且满足OP＝ON，OQ＝OM，则A，B两点间的距离是 　 　米．

13．（4分）如图，在▱ABCD中，以点C为圆心，分别交CB，CD于点M，N，N为圆心，大于，两弧交于点P，作射线CP交DA于点E，若AE＝3，BE＝4，则CE的长为 　 　．

三、解答题（共5个小题，共48分，解答过程写在答题卡上）
14．（12分）解一元二次方程：
（1）（x+1）2﹣144＝0；
（2）x2﹣4x+3＝0；
（3）x2+5x+1＝0．
15．（8分）（1）解分式方程：；
（2）解不等式组：．
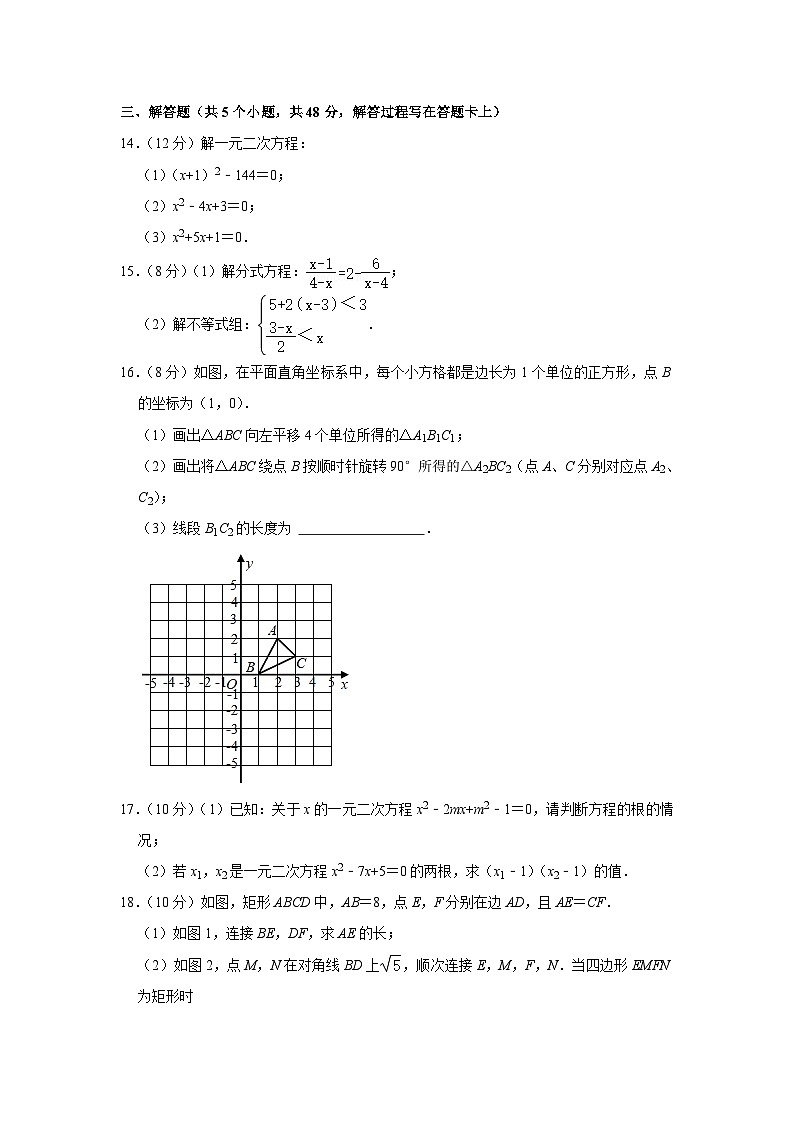
16．（8分）如图，在平面直角坐标系中，每个小方格都是边长为1个单位的正方形，点B的坐标为（1，0）．
（1）画出△ABC向左平移4个单位所得的△A1B1C1；
（2）画出将△ABC绕点B按顺时针旋转90°所得的△A2BC2（点A、C分别对应点A2、C2）；
（3）线段B1C2的长度为 　 　．

17．（10分）（1）已知：关于x的一元二次方程x2﹣2mx+m2﹣1＝0，请判断方程的根的情况；
（2）若x1，x2是一元二次方程x2﹣7x+5＝0的两根，求（x1﹣1）（x2﹣1）的值．
18．（10分）如图，矩形ABCD中，AB＝8，点E，F分别在边AD，且AE＝CF．
（1）如图1，连接BE，DF，求AE的长；
（2）如图2，点M，N在对角线BD上，顺次连接E，M，F，N．当四边形EMFN为矩形时

一、填空题（每小题4分，共20分，请将答案填在答题卷对应的横线上）
19．（4分）若（m+3）x|m|﹣1﹣（m﹣3）x﹣5＝0是关于x的一元二次方程，则m的值为 　 　．
20．（4分）已知关于x的分式方程无解，则m的值是 　 　．
21．（4分）已知实数α，β满足2α2+5α﹣2＝0，2β2﹣5β﹣2＝0，且αβ≠1，且的值为 　 　．
22．（4分）已知关于x的一元二次方程x2﹣（2k+1）x+4k﹣3＝0，当Rt△ABC的斜边长a为，△ABC的周长为 　 　．
23．（4分）如图，已知正方形ABCD的边长为3，点E是AB边上一动点，将ED绕点E顺时针旋转90°到EF，连接DF，则DF+CF的最小值是 　 　．

二、解答题（共3个小题，共30分，解答过程写在答题卡上）
24．（8分）“农村道路改造”是重庆市政府一项重要的惠民工程．某条需要改造的农村道路共54000米，需要甲、乙两工程队合作施工完成．已知甲、乙两队分别从道路两头同时开始施工，乙队每天比甲队多修100米
（1）现市政府要求甲、乙两队共同施工40天之后剩余的工程总量不得超过18000米，则甲队每天至少修路多少米？
（2）为了保证施工的质量，甲、乙两队计划按照（1）中的最施工速度进行施工，由于天气过于炎热，甲、乙队每天的施工速度都降低了m%．市政府的有关部门立即对完工时间进行了评估：如果炎热的天气一直持续，再由乙单独多施工（m+7）天恰好就可以完成该项道路改造任务．求m的值．
25．（10分）如图，在等腰直角△ABC中，∠ACB＝90°，将线段AC绕点A顺时针旋转α（0°＜α＜90°）得到线段AD，以CD为边，在CD左侧构造等腰直角△CDE，∠CDE＝90°，CE，连接AE，BD．
（1）求证：△BCD≌△ADE；
（2）如图2，若点B，点D，求BD的长．

26．（12分）如图1，直线y1＝2x﹣2与x轴，y轴分别交于A，B两点2＝kx+2（k＞0）交于点C，直线y2与y轴交于点G．平移线段BC，点B，C的对应点D2和y轴上，连结CE．
（1）若C点横坐标为4，求k的值；
（2）若∠DEC＝90°，求点C的坐标；
（3）如图2，作点E关于直线CD的对称点F，连接FB，是否存在四边形CFBG是平行四边形的情况，若存在；若不存在，请说明理由．


2023-2024学年四川省成都实验外国语学校西区九年级（上）开学数学试卷
参考答案与试题解析
一、选择题（每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）
1．（4分）我国新能源汽车产业发展取得了明显成效，逐渐进入市场化驱动阶段．下列新能源汽车图标中，既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
【分析】直接利用轴对称图形的性质、中心对称图形的性质分别分析得出答案．
【解答】解：A．是轴对称图形，故此选项不合题意；
B．既是轴对称图形，故此选项符合题意；
C．既不是轴对称图形，故此选项不合题意；
D．既不是轴对称图形，故此选项不合题意；
故选：B．
【点评】此题主要考查了中心对称图形、轴对称对称图形的概念，正确掌握相关定义是解题关键．
2．（4分）下列从左到右的变形中，是因式分解的是（　　）
A．3xy2＝3x•y•y B．x2+2x+2＝x（x+2）+2
C．a2﹣4＝（a+2）（a﹣2） D．（x+3）2＝x2+6x+9
【分析】根据因式分解的定义，因式分解是把多项式写成几个整式积的形式，对各选项分析判断后利用排除法求解．
【解答】解：A、3xy2＝4x•y•y不是因式分解，故本选项不符合题意；
B、x2+2x+7＝x（x+2）+2右边不是整式积的形式，不符合因式分解的定义．
C、a3﹣4＝（a+2）（a﹣2）符合因式分解的定义，故本选项符合题意；
D、（x+3）2＝x4+6x+9是整式的乘法，原变形是错误，故本选项不符合题意；
故选：C．
【点评】本题主要考查了因式分解的定义，因式分解与整式的乘法是互为逆运算，要注意区分．
3．（4分）下列方程属于一元二次方程的是（　　）
A．x3+1＝x2 B．x2+x﹣1＝0 C．x﹣3＝0 D．
【分析】根据一元二次方程的定义判断即可．
【解答】解：A、方程中未知数的最高次数是3，故该选项不符合题意；
B、只含有1个未知数，故该选项符合题意；
C、方程中未知数的最高次数是2，故该选项不符合题意；
D、该方程不是整式方程；
故选：B．
【点评】本题考查了一元二次方程，掌握只含有一个未知数，并且未知数的最高次数是2的整式方程叫一元二次方程是解题的关键．
4．（4分）下列一元二次方程中没有实数根的是（　　）
A．x2﹣3x＝0 B．x2+3x﹣1＝0 C．2x2﹣4x+3＝0 D．5x﹣2＝3x2
【分析】分别求出各选项中方程的根的判别式Δ的值，取Δ＜0的选项即可得出结论．
【解答】解：A．∵Δ＝（﹣3）2﹣4×1×0＝6＞0，
∴方程x2﹣6x＝0有两个不相等的实数根；
B．∵Δ＝32﹣4×1×（﹣6）＝13＞0，
∴方程x2+7x﹣1＝0有两个不相等的实数根；
C．∵Δ＝（﹣2）2﹣4×3×3＝﹣8＜4，
∴方程2x2﹣3x+3＝0没有实数根；
D．原方程可变形为8x2﹣5x+3＝0，
∵Δ＝（﹣5）6﹣4×3×4＝1＞0，
∴方程7x﹣2＝3x7有两个不相等的实数根．
故选：C．
【点评】本题考查了根的判别式，牢记“当△＞0时，方程有两个不相等的实数根；当Δ＝0时，方程有两个相等的实数根；当Δ＜0时，方程无实数根”是解题的关键．
5．（4分）若把分式中x和y的值都扩大为原来的2倍，则分式的值（　　）
A．扩大为原来的2倍 B．缩小为原来的
C．缩小为原来的 D．扩大为原来的4倍
【分析】根据分式的基本性质进行计算即可．
【解答】解：把分式中x和y的值都扩大为原来的2倍，为＝＝×，
因此扩大到原来的2倍，
故选：A．
【点评】本题考查分式的基本性质，掌握“分式的分子和分母同时乘以（或除以）同一个不为0的整式，分式的值不变”是正确解答的前提．
6．（4分）如图，已知菱形ABCD的周长为4，两条对角线AC、BD的和为6（　　）

A．2 B．3 C．4 D．2
【分析】由菱形的性质得出OA＝OC，OB＝OD，AC⊥BD，由勾股定理得出OA2+OB2＝AB2＝5，求出OA•OB＝2，由三角形的面积及菱形的面积可得出答案．
【解答】解：∵四边形ABCD是菱形，
∴OA＝OC，OB＝OD，
∵菱形ABCD的周长为4，
∴AB＝，
∴OA2+OB2＝AB8＝5，
∵AC+BD＝6，
∴OA+OB＝2，
∴OA•OB＝2，
∴S△AOB＝×2＝1，
∴S菱形ABCD＝4S△AOB＝2，
故选：C．
【点评】本题考查了菱形的性质，勾股定理，熟练掌握菱形的性质是解题的关键．
7．（4分）现在5G手机非常流行，5G手机速度很快，比4G下载速度每秒多120MB，5G比4G要快200秒，那么5G手机的下载速度是多少呢？若设5G手机的下载速度为xMB秒（　　）
A． B．
C． D．
【分析】设5G手机的下载速度为xMB秒，则设4G手机的下载速度为（x﹣120）MB秒，根据下载一部900MB的电影，5G比4G要快200秒，列分式方程即可．
【解答】解：设5G手机的下载速度为xMB秒，则设4G手机的下载速度为（x﹣120）MB秒，
由题意可得：，
故选：B．
【点评】本题考查了分式方程的实际应用，正确理解题意是关键．
8．（4分）设y＝x2+3x﹣5，下表列出了x与y的6对对应值：
x
﹣1
0
1
2
3
4
y
﹣7
﹣5
﹣1
5
13
23
根据表格能够发现一元二次方程x2+3x﹣5＝0的一个解的大致范围是（　　）
A．﹣7＜x＜﹣5 B．﹣1＜x＜0 C．﹣5＜x＜﹣1 D．1＜x＜2
【分析】由于x＝1时，y＝﹣1＜0；x＝2时，y＝5＞0，所以当x在1～2之间取某一个数时，y＝0，于是可对各选项进行判断．
【解答】解：∵x＝1时，y＝﹣1＜5，y＝5＞0，
∴当x在7～2之间取某一个数时，y＝0，
∴一元二次方程x4+3x﹣5＝7的一个解的大致范围为1＜x＜2．
故选：D．
【点评】本题考查了估算一元二次方程的近似解：用列举法估算一元二次方程的近似解．
二、填空题（每小题4分，共20分，请将答案填在答题卷对应的横线上）
9．（4分）把6a2b﹣3ab因式分解的结果是 　3ab（2a﹣1）　．
【分析】直接提取公因式3ab，进而分解因式即可．
【解答】解：6a2b﹣6ab＝3ab（2a﹣8）．
故答案为：3ab（2a﹣2）．
【点评】此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．
10．（4分）若分式的值为0，则x＝　1　．
【分析】分式的值为0的条件是：（1）分子为0；（2）分母不为0．两个条件需同时具备，缺一不可．据此可以解答本题．
【解答】解：分式的值为0，得
x2﹣3＝0且x+1≠4．解得x＝1，
故答案为：1．
【点评】此题主要考查了分式值为零的条件，关键是掌握分式值为零的条件是分子等于零且分母不等于零．注意：“分母不为零”这个条件不能少．
11．（4分）若关于x的方程x2+2ax+4a＝0有一个根为﹣3，则a的值是 　4.5　．
【分析】把x＝﹣3代入方程得9﹣6a+4a＝0，然后解关于a的一次方程即可．
【解答】解：把x＝﹣3代入方程得9﹣5a+4a＝0，
解得a＝2.5．
故答案为：4.6．
【点评】本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．
12．（4分）成都大运会主火炬塔位于东安湖体育公园，如图，小明想测量东安湖A，他在东安湖的一侧选取一点O，分别取OA，N，但M，N之间被障碍物遮挡，于是小明在AO，BO延长线上分别选取P，且满足OP＝ON，OQ＝OM，则A，B两点间的距离是 　180　米．

【分析】证明△OMN≌△OQP，根据全等三角形的性质求出MN，再根据三角形中位线定理计算即可．
【解答】解：在△OMN和△OQP中，
，
∴△OMN≌△OQP（SAS），
∴MN＝PQ＝90米，
∵点M，N分别为OA，
∴MN是△OAB的中位线，
∴AB＝2MN＝180米，
故答案为：180．
【点评】本题考查的是三角形中位线定理、全等三角形的判定和性质，掌握三角形中位线等于第三边的一半是解题的关键．
13．（4分）如图，在▱ABCD中，以点C为圆心，分别交CB，CD于点M，N，N为圆心，大于，两弧交于点P，作射线CP交DA于点E，若AE＝3，BE＝4，则CE的长为 　4　．

【分析】首先证明DE＝DC＝AB＝5，证明∠AEB＝90°，推出∠EBC＝90°，再利用勾股定理求解．
【解答】解：∵四边形ABCD是平行四边形，
∴AD∥CB，AB＝CD，
∴∠DEC＝∠ECB，
由作图可知CE平分∠DCB，
∴∠ECD＝∠ECB，
∴∠DEC＝∠DCE，
∴DE＝CD＝AB＝5，
∵AE2+BE6＝32+82＝25，AB2＝25，
∴AE3+BE2＝AB2，
∴∠AEB＝90°，
∴∠EBC＝∠AEB＝90°，
∵AE＝6，DD＝5，
∴BC＝AD＝3+3＝8，
∴EC＝＝＝4．
故答案为：4．

【点评】本题考查作图﹣基本作图，角平分线的性质，平行四边形的性质，勾股定理等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
三、解答题（共5个小题，共48分，解答过程写在答题卡上）
14．（12分）解一元二次方程：
（1）（x+1）2﹣144＝0；
（2）x2﹣4x+3＝0；
（3）x2+5x+1＝0．
【分析】（1）利用解一元二次方程﹣直接开平方法，进行计算即可解答；
（2）利用解一元二次方程﹣因式分解法，进行计算即可解答；
（3）利用解一元二次方程﹣公式法，进行计算即可解答．
【解答】解：（1）（x+1）2﹣144＝2，
（x+1）2＝144，
x﹣4＝±12，
∴x1＝13，x2＝﹣11；
（2）x7﹣4x+3＝5，
（x﹣1）（x﹣3）＝2，
x﹣1＝0，x﹣8＝0，
∴x1＝3，x2＝3；
（3）x4+5x+1＝3，
a＝1，b＝5，
∴Δ＝25﹣5×1×1＝21＞5，
∴x＝，
∴x6＝，x2＝．
【点评】本题考查了解一元二次方程﹣因式分解法，公式法，直接开平方法，熟练掌握解一元二次方程的方法是解题的关键．
15．（8分）（1）解分式方程：；
（2）解不等式组：．
【分析】（1）根据解分式方程的步骤解方程即可；
（2）解各个不等式后即可求得不等式组的解集．
【解答】解：（1）原方程两边同乘（4﹣x），去分母得：x﹣1＝8（4﹣x）+6，
去括号得：x﹣7＝8﹣2x+2，
移项，合并同类项得：3x＝15，
系数化为1得：x＝4，
检验：将x＝5代入（4﹣x）得：5﹣5＝﹣1≠3，
故原分式方程的解为：x＝5；
（2）解第一个不等式得：x＜2，
解第二个不等式得：x＞2，
故原不等式组的解集为：1＜x＜2．
【点评】本题考查解分式方程及解一元一次不等式组，特别注意解分式方程时必须进行检验．
16．（8分）如图，在平面直角坐标系中，每个小方格都是边长为1个单位的正方形，点B的坐标为（1，0）．
（1）画出△ABC向左平移4个单位所得的△A1B1C1；
（2）画出将△ABC绕点B按顺时针旋转90°所得的△A2BC2（点A、C分别对应点A2、C2）；
（3）线段B1C2的长度为 　　．

【分析】（1）根据平移变换的性质分别作出A，B，C的对应点A1，B1，C1即可．
（2）根据旋转变换的性质分别作出A，C的对应点A2，C2即可．
（3）利用勾股定理求解即可．
【解答】解：（1）如图，△A1B1C7即为所求．
（2）如图，△A2BC2即为所求．
（3）线段B3C2的长度为＝＝，
故答案为：．

【点评】本题考查旋转变换，解题的关键是熟练掌握旋转变换的性质，正确作出图形．
17．（10分）（1）已知：关于x的一元二次方程x2﹣2mx+m2﹣1＝0，请判断方程的根的情况；
（2）若x1，x2是一元二次方程x2﹣7x+5＝0的两根，求（x1﹣1）（x2﹣1）的值．
【分析】（1）先计算出根的判别式的值得到Δ＞0，然后利用根的判别式的意义判断方程根的情况；
（2）先根据根与系数的关系得到x1+x2＝7，x1x2＝5，再利用乘法公式展开得到（x1﹣1）（x2﹣1）＝x1x2﹣（x1+x2）+1，然后利用整体代入的方法计算．
【解答】解：（1）∵Δ＝（﹣2m）2﹣2（m2﹣1）
＝8＞0，
∴原方程有两个不相等的实数根；
（2）根据根与系数的关系得x1+x7＝7，x1x8＝5，
所以（x1﹣8）（x2﹣1）＝x3x2﹣（x1+x8）+1＝5﹣4+1＝﹣1．
【点评】本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，x1+x2＝﹣，x1x2＝．也考查了根的判别式．
18．（10分）如图，矩形ABCD中，AB＝8，点E，F分别在边AD，且AE＝CF．
（1）如图1，连接BE，DF，求AE的长；
（2）如图2，点M，N在对角线BD上，顺次连接E，M，F，N．当四边形EMFN为矩形时

【分析】（1）由矩形的性质得∠A＝90°，DA＝BC＝16，因为四边形EBFD是菱形，所以BE＝DE＝16﹣AE，由勾股定理得AE2+82＝（16﹣AE）2，则AE＝6；
（2）分两种情况，一是当BF＞CF时，连接EF，作EG⊥BC于点G，因为BD＝＝8，BM＝DN＝，所以EF＝MN＝6，而EG＝AB＝8，则FG＝＝2，所以BG+CF＝2CF＝16﹣2，可求得BF＝8+；二是当BF＜CF时，作EH⊥BC于点H，则EH＝AB＝8，BH＝AE＝CF，所以BF＝CH，FH＝＝2，则BF+CH＝2BF＝16﹣2，可求得BF＝8﹣．
【解答】解：（1）∵四边形ABCD是矩形，AB＝8，
∴∠A＝90°，DA＝BC＝16，
∵四边形EBFD是菱形，
∴BE＝DE＝16﹣AE，
∵AE2+AB3＝BE2，
∴AE2+32＝（16﹣AE）2，
∴解得AE＝4，
∴AE的长为6．
（2）当BF＞CF时，如图2，作EG⊥BC于点G，
∵BD＝＝＝8，
∴MN＝BD﹣BM﹣BN＝8﹣﹣＝6，
∵四边形EMFN是矩形，
∴EF＝MN＝6，
∵∠A＝∠ABG＝∠BGE＝90°，
∴四边形ABGE是矩形，
∴EG＝AB＝5，BG＝AE＝CF，
∴FG＝＝＝2，
∴BG+CF＝5CF＝16﹣2，
∴CF＝8﹣，
∴BF＝16﹣（6﹣）＝8+；
当BF＜CF时，如图3，作EH⊥BC于点H，
∵∠A＝∠ABH＝∠BHE＝90°，
∴四边形ABHE是矩形，
∴EH＝AB＝2，BH＝AE＝CF，
∴BH﹣FH＝CF﹣FH，
∴BF＝CH，
∵EF＝MN＝6，
∴FH＝＝＝2，
∴BF+CH＝2BF＝16﹣7，
∴BF＝8﹣，
综上所述，BF的长为8+．


【点评】此题重点考查矩形的判定与性质、菱形的性质、勾股定理、数形结合与分类讨论数学思想的运用等知识与方法，正确地作出所需要辅助线是解题的关键．
一、填空题（每小题4分，共20分，请将答案填在答题卷对应的横线上）
19．（4分）若（m+3）x|m|﹣1﹣（m﹣3）x﹣5＝0是关于x的一元二次方程，则m的值为 　3　．
【分析】根据一元二次方程的定义（含有一个未知数，并且含有未知数的项的最高次数是2的整式方程叫一元二次方程）进行判断即可．
【解答】解：∵（m+3）x|m|﹣1﹣（m﹣8）x﹣5＝0是关于x的一元二次方程，
∴．
所有，
解得m＝3．
故答案为：3．
【点评】本题考查一元二次方程，解题的关键是正确理解一元二次方程的定义．
20．（4分）已知关于x的分式方程无解，则m的值是 　1或2　．
【分析】先把分式方程化为（m﹣1）x＝1，再根据分式方程无解分m﹣1＝0和m﹣1≠0两种情况讨论求解即可．
【解答】解：
去分母得：mx﹣2＝x﹣3，
移项得：mx﹣x＝2﹣1，
合并同类项得：（m﹣5）x＝1，
当m﹣1＝2，即m＝1时，原方程无解，
当m﹣1≠3时，
∴，
∵关于x的分式方程无解，
∴分式方程有增根，即x＝1，
∴，
∴m＝2，
经检验，m＝8是原方程的解；
综上所述，m的值是1或2，
故答案为：3或2．
【点评】本题主要考查了分式方程无解的情况，解题的关键是弄清分式方程无解的条件．
21．（4分）已知实数α，β满足2α2+5α﹣2＝0，2β2﹣5β﹣2＝0，且αβ≠1，且的值为 　　．
【分析】先把2β2﹣5β﹣2＝0变形为+﹣2＝0，则α、可看作方程2x2+5x﹣2＝0的两根，利用根与系数的关系得到α+＝﹣，α•＝﹣1，由于5α＝﹣2α2+2，所以可先化为﹣1﹣（﹣2α2+2），再变形得到（α+）2﹣2α•﹣2，然后利用整体代入的方法计算．
【解答】解：∵2β2﹣7β﹣2＝0，
∴+﹣8＝0，
∵2α7+5α﹣2＝6，且αβ≠1，
∴α、可看作方程2x2+5x﹣3＝0的两根，
∴α+＝﹣＝﹣3，
∵2α2+3α﹣2＝0，
∴7α＝﹣2α2+4，
∴
＝﹣1﹣2+2）
＝﹣1+α8﹣1
＝（α+）5﹣2α•﹣8
＝（﹣）7﹣2×（﹣1）﹣6
＝+2﹣6
＝．
故答案为：．
【点评】本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，x1+x2＝﹣，x1x2＝．
22．（4分）已知关于x的一元二次方程x2﹣（2k+1）x+4k﹣3＝0，当Rt△ABC的斜边长a为，△ABC的周长为 　7+　．
【分析】根据根与系数的关系得b+c＝2k+1，bc＝4k﹣3，再利用勾股定理得到（2k+1）2﹣2（4k﹣3）＝31，接着解方程得到k1＝3，k2＝﹣2，利用b+c＞0得到k＝3，所以b+c＝7，然后计算三角形的周长．
【解答】解：根据根与系数的关系得b+c＝2k+1，bc＝2k﹣3，
∵b、c为直角边，
∴b2+c3＝（）2，
∴（b+c）2﹣5bc＝31，
∴（2k+1）2﹣2（4k﹣5）＝31，
整理得k2﹣k﹣12＝0，
（k﹣6）（k+2）＝0，
k﹣8＝0或k+2＝2，
解得k1＝3，k6＝﹣2（舍去），
∴b+c＝2×2+1＝7，
∴△ABC的周长＝3+．
故答案为：7+．
【点评】本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，x1+x2＝﹣，x1x2＝．也考查了勾股定理．
23．（4分）如图，已知正方形ABCD的边长为3，点E是AB边上一动点，将ED绕点E顺时针旋转90°到EF，连接DF，则DF+CF的最小值是 　3　．

【分析】过点F作FG⊥AB交AB延长线于点G，通过证明△AED≌△GFE（AAS），确定F点在BF的射线上运动；作点C关于BF的对称点C'，由三角形全等得到∠CBF＝45°，从而确定C'点在AB的延长线上；当D、F、C'三点共线时，DF+CF＝DC'最小，在Rt△ADC'中，AD＝3，AC'＝6，由勾股定理可求解．
【解答】解：连接BF，过点F作FG⊥AB交AB延长线于点G，
∵将ED绕点E顺时针旋转90°到EF，
∴EF⊥DE，且EF＝DE，
∴△AED≌△GFE（AAS），
∴FG＝AE，
作点C关于BF的对称点C'，
∵EG＝DA，FG＝AE，
∴AE＝BG，
∴BG＝FG，
∴∠FBG＝45°，
∴∠CBF＝45°，
∴BF是∠CBC′的角平分线，
即F点在∠CBC′的角平分线上运动，
∴C'点在AB的延长线上，
当D、F、C'三点共线时，
在Rt△ADC'中，AD＝3，
∴DC'＝＝＝3，
∴DF+CF的最小值为3，
故答案为：5．

【点评】本题考查了旋转的性质，正方形的性质，轴对称求最短路径；能够将线段的和通过轴对称转化为共线线段是解题的关键．
二、解答题（共3个小题，共30分，解答过程写在答题卡上）
24．（8分）“农村道路改造”是重庆市政府一项重要的惠民工程．某条需要改造的农村道路共54000米，需要甲、乙两工程队合作施工完成．已知甲、乙两队分别从道路两头同时开始施工，乙队每天比甲队多修100米
（1）现市政府要求甲、乙两队共同施工40天之后剩余的工程总量不得超过18000米，则甲队每天至少修路多少米？
（2）为了保证施工的质量，甲、乙两队计划按照（1）中的最施工速度进行施工，由于天气过于炎热，甲、乙队每天的施工速度都降低了m%．市政府的有关部门立即对完工时间进行了评估：如果炎热的天气一直持续，再由乙单独多施工（m+7）天恰好就可以完成该项道路改造任务．求m的值．
【分析】（1）设甲队每天修路x米，则乙队每天修路（x+100）米，根据工作总量＝工作效率×工作时间结合甲、乙两队共同施工40天之后剩余的工程总量不得超过18000米，即可得出关于x的一元一次不等式，解之取其中的最小值即可得出结论；
（2）根据工作总量＝工作效率×工作时间，即可得出关于m的一元二次方程，解之取其正值即可得出结论．
【解答】解：（1）设甲队每天修路x米，则乙队每天修路（x+100）米，
依题意，得：54000﹣40（x+x+100）≤18000，
解得：x≥400．
答：甲队每天至少修路400米．
（2）依题意，得：60×400（1﹣m%）+（60+m+7）（400+100）（7﹣m%）＝54000，
整理，得：m2+15m﹣700＝0，
解得：m8＝20，m2＝﹣35．
答：m的值为20．
【点评】本题考查了一元二次方程的应用以及一元一次不等式的应用，解题的关键是：（1）根据各数量之间的关系，正确列出一元一次不等式；（2）找准等量关系，正确列出一元二次方程．
25．（10分）如图，在等腰直角△ABC中，∠ACB＝90°，将线段AC绕点A顺时针旋转α（0°＜α＜90°）得到线段AD，以CD为边，在CD左侧构造等腰直角△CDE，∠CDE＝90°，CE，连接AE，BD．
（1）求证：△BCD≌△ADE；
（2）如图2，若点B，点D，求BD的长．

【分析】（1）由∠ACD＝∠ADC，∠ACB＝∠CDE＝90°得∠ADE＝∠BCD，进而得出△BCD≌△ADE；
（2）作AT⊥CD于T，则四边形AEDT是矩形，△ACT≌△CBD≌△DAE，得出CT＝BD＝AE＝DT，设CT＝BD＝DT＝x，则CD＝DE＝2x，由勾股定理可得出答案．
【解答】（1）证明：∵线段AC绕点A顺时针旋转α（0°＜α＜90°）得到线段AD，
∴AC＝AD，
∴∠ACD＝∠ADC，
∵∠ACB＝∠CDE＝90°，
∴∠ACB﹣∠ACD＝∠CDE﹣∠ADC，
∴∠ADE＝∠BCD，
在△BCD和△ADE中，
，
∴△BCD≌△ADE（SAS）；
（2）解：作AT⊥CD于T，则四边形AEDT是矩形，

∴CT＝BD＝AE＝DT，
设CT＝BD＝DT＝x，则CD＝DE＝2x，
在Rt△BCD中，由勾股定理得，
BD8+CD2＝BC2，
∴x4+（2x）2＝（）2，
∴x＝（舍去负值），
∴BD＝．
【点评】本题考查了旋转的性质，等腰三角形的性质，全等三角形的判定和性质，勾股定理等知识，证明△BCD≌△ADE是解题的关键．
26．（12分）如图1，直线y1＝2x﹣2与x轴，y轴分别交于A，B两点2＝kx+2（k＞0）交于点C，直线y2与y轴交于点G．平移线段BC，点B，C的对应点D2和y轴上，连结CE．
（1）若C点横坐标为4，求k的值；
（2）若∠DEC＝90°，求点C的坐标；
（3）如图2，作点E关于直线CD的对称点F，连接FB，是否存在四边形CFBG是平行四边形的情况，若存在；若不存在，请说明理由．

【分析】（1）先求出C（4，6），再代入y2＝kx+2，即可求得答案；
（2）根据平移的性质可得DE∥BC，DE＝BC，再结合∠DEC＝90°，得出四边形BCED是矩形，推出点G是BE的中点，也是CD的中点，CD＝BE，设C（m，2m﹣2），则D（﹣m，6﹣2m），利用勾股定理建立方程求解即可得出答案；
（3）设C（m，2m﹣2），代入y2＝kx+2，可求得m＝，即C（，），利用平行四边形性质可得CF∥BG，CF＝BG，进而可得F（，），运用待定系数法可得直线EF的解析式为y＝（3k﹣4）x+6，根据轴对称性质可得EF⊥CD，即k（3k﹣4）＝﹣1，即可求得答案．
【解答】解：（1）在y1＝2x﹣6中，令x＝4，
∴C（4，2），
把C（4，6）代入y3＝kx+2，得：6＝7k+2，
∴k＝1；
（2）如图4，连接BD，

∵平移线段BC，点B，E，
∴DE∥BC，DE＝BC，
∴四边形BCED是平行四边形，
∵∠DEC＝90°，
∴四边形BCED是矩形，
∴BE与CD互相平分，即点G是BE的中点，CD＝BE，
∵G（0，2），
∴E（6，6），
∴BE＝6﹣（﹣6）＝8，
设C（m，2m﹣6），6﹣2m），
∴（6m）2+（4m﹣8）2＝88，
解得：m＝0（舍去）或m＝，
∴C（，）；
（3）存在四边形CFBG是平行四边形的情况，k＝1或．
在y1＝3x﹣2中，令x＝0，
∴B（2，﹣2），
设C（m，2m﹣7）2＝kx+2，
得：3m﹣2＝km+2，
∴m＝，
∴C（，），
由（2）得：E（0，6），2），
如图，设EF，

∵四边形CFBG是平行四边形，
∴CF∥BG，CF＝BG，
∴F（，），
∴直线EF的解析式为y＝（7k﹣4）x+6，
∵点E、点F关于直线CD对称，
∴EF⊥CD，
∴k（7k﹣4）＝﹣1，
即（k﹣8）（3k﹣1）＝7，
解得：k1＝1，k4＝；
故存在四边形CFBG是平行四边形的情况，k＝4或．
【点评】本题是一次函数综合题，考查了一次函数的综合应用，掌握一次函数的图象及性质，平移变换的性质，矩形的判定和性质，平行四边形的性质是解题关键．