数学基础模块上册4.8 已知三角函数值求角教案

授课题目

4.8 已知三角函数值求角

选用教材

高等教育出版社《数学》

（基础模块上册）

授课

时长

2 课时

授课

类型

新授课

教学提示

本课将结合计算工具和诱导公式，学习由已知三角函数值求符合条件的角，学习特殊的三角函数值与[0,2π]范围内角的对应关系，并用运算

工具进行有关的三角运算．

教学目标

知道由三角函数值求指定范围内的角的原理，能利用诱导公式求出指定范围内满足三角函数值的特殊角，逐步提升数学运算和逻辑推理等核心素养；知道应用计算器求三角函数值的方法，能够应运用计算器求

出指定范围内满足三角函数值的角，逐步提升数学运算等核心素养．

教学

重点

已知特殊角的三角函数值求角．

教学

难点

掌握已知正弦值、余弦值、正切值求角的方法．

教学

环节

教学内容

教师

活动

学生

活动

设计

意图

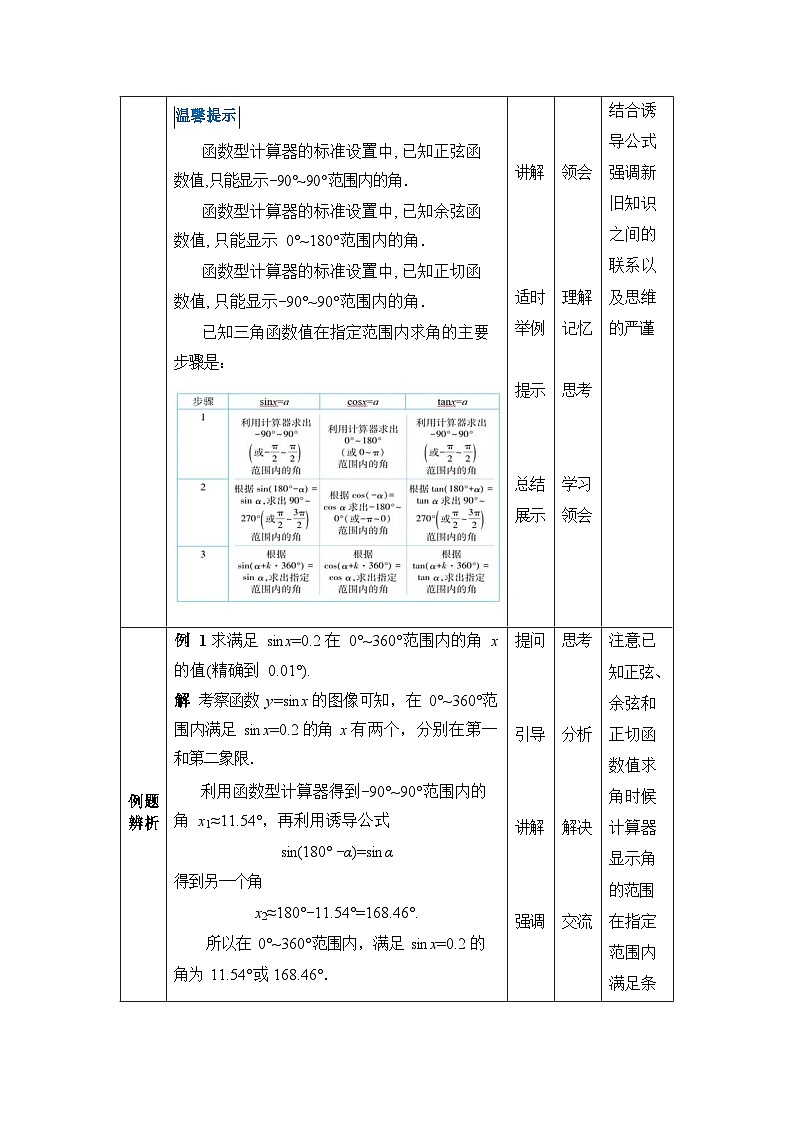
情境导入

如何求出正弦函数 y=sinx 与直线 y= 1 在区

4

间[0,2π]上的交点？

提问启发引导

思考作答交流

探求知识之间的联系数形结合说明问题

探索新知

要求这个交点，实际上就求sin x  1 ，x∈[0,

4

2π]的解.也就是已知三角函数值求指定范围内的角.

首先利用科学型计算器求满足sin x  1 ，x

4

∈[0, 2π]的解，将结果保留到小数点后第 4 位. 步骤：

(1) 将函数型计算器设为弧度制模式：

讲解

示范操作

理解

学习模仿

将未知问题转化为已有知识发现知识之间的联系

SHIFT→MODE SETUP→4

(2)  SHIFT→sin→0→.→2→5→=显示结果

0.2526802551. 此时显示的是  ~  范围内的

2 2

角, 即 x1≈0.2527．

(3)    根据诱导公式 sin(π-α)=sinα, 得到

x2≈π-0.2527≈2.8889.

因此, 正弦函数 y=sinx 与直线 y= 1 在区间

4

[0, 2π]上的交点为(0.2527，0.25)和(2.8889, 0.25)．

探索与发现

求正弦函数 y=sinx 与直线 y= 1 在区间[0,2π]

2

上的交点.

对特殊的三角函数值容易求出指定范围内的角，对一般的三角函数值，我们则需要借助函数型计算器与诱导公式求出指定范围内的 角．

已知三角函数值，利用计算器求角可以按如下流程操作：

设定角度或弧度计算模式→按键 SHIFT→

→输入三角函数值→按键=显示

角．

如果要求指定范围内的角，一般需要使用诱导公式．

及时巩

固

提问

操作

初步学

习用计

算器求

角的一

讲解

思考

般流程

说明

理解

温馨提示

函数型计算器的标准设置中, 已知正弦函数值,只能显示-90°~90°范围内的角．

函数型计算器的标准设置中, 已知余弦函数值, 只能显示 0°~180°范围内的角．

函数型计算器的标准设置中, 已知正切函数值, 只能显示-90°~90°范围内的角．

已知三角函数值在指定范围内求角的主要步骤是：

结合诱

导公式

讲解

领会

强调新

旧知识

之间的

联系以

适时

理解

及思维

举例

记忆

的严谨

提示

思考

总结

学习

展示

领会

例 1 求满足 sinx=0.2 在 0°~360°范围内的角 x

的值(精确到 0.01°).

解 考察函数 y=sinx 的图像可知，在 0°~360°范围内满足 sinx=0.2 的角 x 有两个，分别在第一和第二象限．

利用函数型计算器得到-90°~90°范围内的角 x1≈11.54°，再利用诱导公式

sin(180°-α)=sinα

得到另一个角

x2≈180°-11.54°=168.46°.

所以在 0°~360°范围内，满足 sinx=0.2 的角为 11.54°或 168.46°．

提问

思考

注意已

知正弦、

余弦和

引导

分析

正切函

数值求

例题

角时候

辨析

讲解

解决

计算器

显示角

的范围

强调

交流

在指定

范围内

满足条

例 2 已知 sinx＝  1 ，且 x∈[0,2π]，求角 x 的值．

2

解 由函 y=sinx 的图像可知，在区间[0,2π]上满

足 sinx＝  1 的角 x 有两个，分别在第三和第四

2

象限．

先求0    上满足sin x= 1 的角，得 x=  ．

，

 2  2 6

由 sin(π＋α)＝-sinα＝  1 得第三象限的角

2

x1＝ + ＝  ；

6 6

由 sin(2π-α)＝sin(-α)＝-sinα＝  1 得第四象

2

限的角 x2＝   ＝ ；

6 6

所以在区间[0,2π]上满足 sinx=  1 的角为 

2 6



和 .

6

探究与发现

求下列特殊的三角函数值在[0,2π]上的角 x 的值.

例 3 已知 cosx=0.2，求在-180°~180°范围内的角

x 的值（精确到 0.01°）．

件的角

可能不

提问

思考

止一个

引导

分析

讲解

解决

强调利

强调

交流

用特殊

函数值

求角也

是常用

方法

加强计

算器的

提问

思考

使用

引导

分析

讲解

解决

强调

交流

加强计

算器的

使用

解 由函数 y=cosx 的图像可知，在-180°~180°范围内满足 cosx=0.2 的角 x 有两个分别在第一和第四象限．利用函数型计算器得到在 0°~180°范围内的角为

x1≈78.46°.

由诱导公式 cos(-α)=cosα，得到-180°~0°范围内的角为

x2≈-78.46°.

所以，在-180°~180°范围内，满足 cosx=0.2 的角为 78.46°和-78.46°.

例 4 已知 tanx=0.2，求在 0°~360°范围内的角 x 的值（精确到 0.01°）．

解 利用函数型计算器，由 tanx=0.2  得到-

90°~90°范围内的角

x1≈11.31°.

利用诱导公式 tan(180   )  tan ，得到

90°~270°内的角为

x2≈180°+11.31°=191.31°.

所以，在 0°~360°范围内，满足 tanx=0.2 的角为 11.31°或 191.31°．

探究与发现

海水受日月的引力，在一定的时候发生涨落的现象称为潮，早潮为潮，晚潮为汐. 通常情况下，船在涨潮时驶进航道，靠近码头；卸货后， 在落潮时返回海洋.若某一天港口的水深 y(单位:m)与时间 t(单位:h)的关系可用函数

y  2.5 sin 4 x  5, x [0, 24]

31

近似表示.某船的吃水深度(船底与水面的距离)

提问

思考

引导

分析

讲解

解决

展示数

学知识

强调

交流

的实际

应用加

深对知

提问

思考

识的理

解

引导

分析

讲解

解决

强调

交流

提出

思考

问题

交流

为 4m，安全条例规定至少有 1.5m 的安全间隙

(船底与洋底的距离)，求该船在这一天的哪个时刻能进入港口？在港口能停留多久？

练习 4.8

1．在 0°~360°范围内，利用科学型计算器求适合下列条件的 x(精确到 0.01°)：

(1) sinx=0.5736； (2) sinx=－0.7181；

(3) cosx=－0.6； (4) tanx=0.75.

2. 在[0,2π]内，利用函数型计算器求适合下列条件的 x(精确到 0. 01)：

(1) sinx=0.7； (2) sinx=－0.7；

(3) cosx=－0.4； (4) tanx=2.

3．在[0,2π]内，求适合下列条件的特殊角 x

的值：

(1)   sin x  3 ； (2) sin x      3 ；

2 2

(3)   cos x  3 ； (4) tanx=－1．

2

提问

思考

及时掌

握学生

的知识

掌握情

巡视

动手

况，查漏

求解

补缺

巩固

练习

指导

交流

引导

回忆

培养学

归纳

生总结

总结

提问

反思

学习过

程能力

1.书面作业：完成课后习题和学习与训练；

说明

记录

继续探

布置

2.查漏补缺：根据个人情况对课题学习复习与回

究

作业

顾;

延伸学

3.拓展作业：阅读教材扩展延伸内容

习