专题06 整式的加减-【挑战压轴题】2022-2023学年七年级数学上册压轴题专题精选汇编（人教版）

这是一份专题06 整式的加减-【挑战压轴题】2022-2023学年七年级数学上册压轴题专题精选汇编（人教版），文件包含七年级数学上册专题06整式的加减原卷版docx、七年级数学上册专题06整式的加减解析版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。

2022-2023学年人教版数学七年级上册压轴题专题精选汇编
专题06 整式的加减
考试时间：120分钟 试卷满分：100分
一．选择题（共10小题，满分20分，每小题2分）
1．（2分）（2022七上·城固期末）下列说法中，正确的是（　　）
A．多项式 是二次三项式
B．单项式 的系数是
C．单项式 和 是同类项
D． 是单项式
【答案】C
【完整解答】解：A、多项式 是三次三项式，故原说法错误；
B、单项式 的系数是 ，故原说法错误；
C、单项式 和 是同类项，故原说法正确；
D、 是多项式，故原说法错误；
故答案为：C.
【思路引导】根据多项式的项与次数的概念可判断A；单项式的系数：单项式中的数字因数叫做这个单项式的系数，据此判断B；根据同类项是字母相同且相同字母的指数也相同的项可判断C；根据数字与字母的乘积为单项式，单独的一个数或字母也是单项式，据此判断D.
2．（2分）（2022七上·汇川期末）某商店在甲批发市场以每包a元的价格进了50包茶叶，又在乙批发市场以每包b元（a＞b）的价格进了同样的70包茶叶，如果以每包 元价格全部卖出这种茶叶，那么这家商店（　　）
A．盈利了 B．亏损了
C．不盈不亏 D．盈亏不能确定
【答案】A
【完整解答】解：∵a＞b，
∴（50+70）× -（50a+70b）
=60a+60b-50a-70b
=10a-10b
=10（a-b）＞0，
∴这家商店盈利了，
故答案为：A.
【思路引导】根据题意计算出售价与成本的差值，然后由a＞b，即可得解.
3．（2分）（2021七上·洪山期末）已知数a，b，c在数轴上的位置如图所示，化简|a ＋ b| － |a － b| ＋ |a ＋ c|的结果为（　　）

A．－a－c B．－a－b－c C．－a－2b－c D．a－2b＋c
【答案】C
【完整解答】解：通过数轴得到a＜0，c＞0，b＞0，|a|＞|c|＞|b|，
∴a+b＜0，a－b＜0，a＋c＜0
∴|a＋b| － |a－b| ＋ |a＋c|＝-a-b＋a－b﹣a-c＝－a－2b－c.
故答案为：C.
【思路引导】根据数轴可得：a<0 4．（2分）（2021七上·巢湖期末）把如图1的两张大小相同的长方形卡片放置在图2与图3中的两个相同大长方形中，已知这两个大长方形的长比宽长20cm，若记图2中阴影部分的周长为C1，图3中阴影部分的周长为C2，那么C1-C2=（　　）

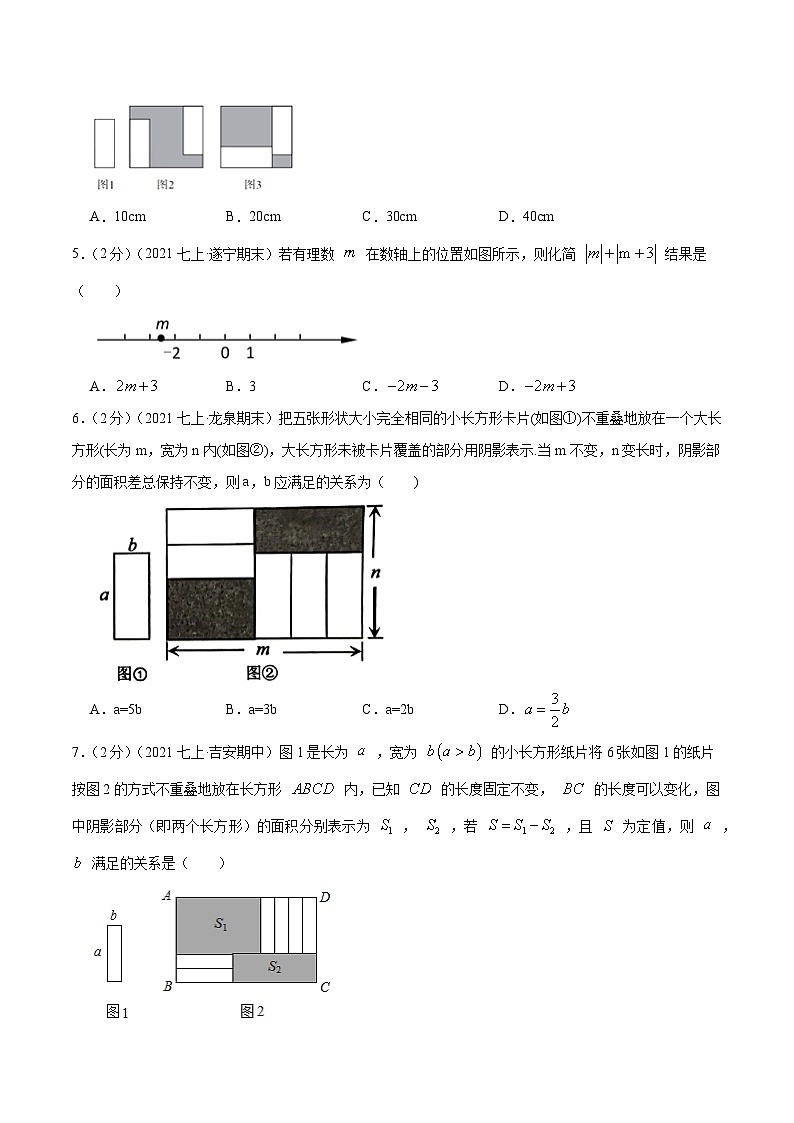
A．10cm B．20cm C．30cm D．40cm
【答案】D
【完整解答】解：设图2与图3中的大长方形的宽为acm，则长为cm，
图1中的长方形长为xcm，宽为ycm，
由图2可知：；
由图3可知：，
，
，
，
，
则（cm），
故答案为：D．
【思路引导】根据题意和图形，设图2与图3中的大长方形的宽为acm，则长为cm，图1中的长方形长为xcm，宽为ycm，再表示出阴影部分的周长；图3可知：，，再作差即可。
5．（2分）（2021七上·遂宁期末）若有理数 在数轴上的位置如图所示，则化简 结果是（　　）

A． B．3 C． D．
【答案】B
【完整解答】解：观察数轴得 且m＞-3（即m+3＞0）
∴
∴ .
故答案为：B.
【思路引导】根据数轴可得-30，然后根据绝对值的性质以及合并同类项法则进行化简.
6．（2分）（2021七上·龙泉期末）把五张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个大长方形(长为m，宽为n内(如图②)，大长方形未被卡片覆盖的部分用阴影表示.当m不变，n变长时，阴影部分的面积差总保持不变，则a，b应满足的关系为（　　)

A．a=5b B．a=3b C．a=2b D．
【答案】B
【完整解答】解：如图右上角阴影的长为3b，宽为n-a，左下角的阴影的长为a，宽设为n-2b，
∴两阴影面积之差S=3b·（n-a）-a·（n-2b）=3bn-3ab-an+2ab=（3b-a）·n-ab，
∵当m不变，n变长时，阴影部分的面积差总保持不变，
∴3b-a=0，即a=3b，
故答案为：B.

【思路引导】利用图②小长方形、阴影和大长方形包含关系可得，右上角阴影的长为3b，宽为n-a，左下角的阴影的长为a，宽设为n-2b，通过作差表示出两阴影面积之差S，再根据整式混合运算的法则进行化简并利用 m不变，n变长时，阴影部分的面积差总保持不变判断出3b-a=0，即可求出3b=a.
7．（2分）（2021七上·吉安期中）图1是长为 ，宽为 的小长方形纸片将6张如图1的纸片按图2的方式不重叠地放在长方形 内，已知 的长度固定不变， 的长度可以变化，图中阴影部分（即两个长方形）的面积分别表示为 ， ，若 ，且 为定值，则 ， 满足的关系是（　　）

A． B． C． D．
【答案】A
【完整解答】解：设BC=n，
则S1=a（n-4b），S2=2b（n-a），
∴S=S1-S2=a（n-4b）-2b（n-a）=（a-2b）n-2ab，
∵当BC的长度变化时，S的值不变，
∴S的取值与n无关，
∴a-2b=0，
即a=2b．
故答案为：A．

【思路引导】设BC=n，则S1=a（n-4b），S2=2b（n-a），再根据图形可得S=S1-S2=a（n-4b）-2b（n-a）=（a-2b）n-2ab，结合“当BC的长度变化时，S的值不变”可得a-2b=0，即可得到答案。
8．（2分）（2021七上·瑞安期末）将图1中周长为32的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形，并将它们按图2的方式放入周长为48的长方形中，则没有覆盖的阴影部分的周长为（　　）

A．16 B．24 C．30 D．40
【答案】D
【完整解答】解：设1号正方形的边长为x，2号正方形的边长为y，则3号正方形的边长为x+y，4号正方形的边长为2x+y，5号长方形的长为3x+y，宽为y-x，
由图1中长方形的周长为32，可得，y+2（x+y）+（2x+y）=16，
解得：x+y=4，
如图，
.
∵图2中长方形的周长为48，
∴AB+2（x+y）+2x+y+y-x=24，
∴AB=24-3x-4y，
根据平移得：没有覆盖的阴影部分的周长为四边形ABCD的周长，
∴2（AB+AD）=2（24-3x-4y+x+y+2x+y+y-x）=2（24-x-y）=48-2（x+y）=48-8=40，
故答案为：D.
【思路引导】设1号正方形的边长为x，2号正方形的边长为y,利用长方形的周长为32，化简得x+y=4，再利用长方形的周长为48，得AB=24-3x-4y，利用平移知没有覆盖的阴影部分的周长为四边形ABCD的周长，求得周长为40.
9．（2分）（2020七上·景德镇期中）记 ，则 （　　）
A．一个偶数 B．一个质数
C．一个整数的平方 D．一个整数的立方
【答案】C
【完整解答】解：∵ ，
∴ ，
∴ ，
∴ ，
∴ ，
∴ 是一个整数的平方；
故答案为：C.

【思路引导】本题利用平方差公式计算即可，关键在等式两边同时乘（3-1）。
10．（2分）（2020七上·正定期中）为求1+2+22+23+…+22015的值，可令S=1+2+22+23+…+22015，则2S=2+22+23+…+22016，因此2S﹣S=22016﹣1.仿照以上推理，计算出1+5+52+53+…+52015的值为（　　）
A．52015﹣1 B．52016﹣1 C． D．
【答案】D
【完整解答】设a =1+5+52+53+…+52015，则5a=5（1+5+52+53+…+52015）=5+52+53+…+52015+52016，
∴5a-a=（5+52+53+…+52015+52016）-（1+5+52+53+…+52015）=52016-1，
即a= .
故答案为：D.
【思路引导】设a =1+5+52+53+…+52015①，可得5a=5（1+5+52+53+…+52015）=5+52+53+…+52015+52016②，利用②-①即可求出结论.
二．填空题（共10小题，满分20分，每题2分）
11．（2分）（2022七上·句容期末）如果单项式 与 的和仍是单项式，则 的值为　 　.
【答案】-4
【完整解答】解：由题意可知： 与 是同类项，
∴a+b=2，b=3，
∴a=-1，
∴a-b=-1-3=-4.
故答案为：-4.
【思路引导】根据同类项是字母相同且相同字母的指数也相同的项可得a+b=2，b=3，求出a的值，然后根据有理数的减法法则进行计算.
12．（2分）（2021七上·白银期末）若 ，则 的值是　 　.
【答案】4
【完整解答】解：根据题意得： 和 是同类项，
∴ ，
∴ .
故答案为：4.
【思路引导】据题意可知-2xym和xny3是同类项，而同类项是字母相同且相同字母的指数也相同的项，据此可得m=3，n=1，然后利用有理数的加法法则进行计算.
13．（2分）（2021七上·烈山期末）多项式与相加后，不含二次项，则常数的值是　 　．
【答案】
【完整解答】解：+
=
∵不含二次项，
∴12m+36=0，
∴m=-3，
故答案为：-3．
【思路引导】先利用合并同类项求出+=，再利用“不含二次项”可得12m+36=0，再求出m的值即可。
14．（2分）（2021七上·澄海期末）如图，将边长为m的正方形纸片沿虚线剪成两块正方形和两块长方形，若拿掉边长为n的小正方形后，再把剩下的三块图形拼成一块长方形，则这块长方形周长为　 　．

【答案】4m
【完整解答】解：新长方形的周长＝2[（m+n）+（m﹣n）]＝4m．
【思路引导】根据题意列出算式2[（m+n）+（m﹣n）]，再计算即可。
15．（2分）（2021七上·海珠期末）某小区要打造一个长方形花圃，已知花圃的长为（a+2b）米，宽比长短b米，则花圃的周长为 　 　米（请用含a、b的代数式表示）．
【答案】（4a+6b）
【完整解答】解：已知花圃的长为米，宽比长短b米，则花圃的宽为米，
∴花圃周长为：米，
故答案为：．
【思路引导】长方形的周长=（长+宽）×2，据此计算即可.
16．（2分）（2020七上·济南期中）将7张相同的小长方形纸片（如图1所示）按图2所求的方式不重叠的放在长方形 内，未被覆盖的部分恰好被分割为两个长方形，面积分别为 ，已知小长方形纸片的长为 ，宽为 ，且 ．若 长度不变， 变长，将这7张小长方形纸片还按照同样的方式放在新的长方形 内，而 的值总保持不变，则 满足的关系是　 　．

【答案】a=4b
【完整解答】解：设S1的长为x，则宽为4b，S2的长为y，则宽为a，
则AB=4b+a，AD=y+3b，
∵x+a=y+3b，
∴y-x=a-3b，
S1与S2的差=ay-4bx=ay-4b（y-a+3b）=（a-4b）y+4ab-12b2，
∴a-4b=0，
即a=4b．
故答案为：a=4b．
【思路引导】表示出左上角与右下角部分的面积，求出它们的差，根据它们的差与AD无关即可求出a与b的关系式．
17．（2分）（2020七上·亳州月考）数a，b，c 在数轴上的位置如图所示．化简：2|b﹣a|﹣|c﹣b|+|a+b|=　 　．

【答案】3a﹣2b+c
【完整解答】由数轴可知：c＜b＜a，
b﹣a＜0，c﹣b＜0，a+b＞0，
则原式=﹣2（b﹣a）+（c﹣b）+（a+b）
=﹣2b+2a+c﹣b+a+b
=3a﹣2b+c．
故答案为3a﹣2b+c．
【思路引导】根据数轴可得c＜b＜a，再判断绝对值式子里是大于0还是小于0，最后去绝对值计算即可。
18．（2分）我们定义三个有理数之间的新运算法则“⊕”：a⊕b⊕c＝ （|a﹣b﹣c|+a+b+c），如：1⊕（﹣2）⊕3＝ [|1﹣（﹣2）﹣3|+1+（﹣2）+3]＝l，在﹣2，﹣4，﹣5，0，2，5，6这7个数中，任意取三个数作为a，b，c的值，进行“a⊕b⊕c“运算，求在所有计算的结果中的最大值是　 　.
【答案】11
【完整解答】当a﹣b﹣c≥0时，a⊕b⊕c＝ （a﹣b﹣c+a+b+c）＝a，此时最大值是a＝6；
当a﹣b﹣c＜0时，a⊕b⊕c＝ （﹣a+b+c+a+b+c）＝b+c，此时最大值为b+c＝11；
∵11＞6，
∴所有计算的结果中的最大值是11，
故答案为：11.
【思路引导】分别求出当a﹣b﹣c≥0时，当a﹣b﹣c＜0时的最大值，然后比较即可.
19．（2分）有一道题目是一个多项式减去x2＋14x－6，小强误当成了加法计算，结果得到2x2－x＋3，则原来的多项式是　 　．
【答案】x2－15x＋9
【完整解答】解：依题可得：
（2x2－x＋3）-（x2＋14x－6），
=2x2－x＋3-x2-14x+6，
=x2－15x＋9.
故答案为：x2－15x＋9.
【思路引导】加数=和-另一个加数，根据题意列出代数式，再由去括号法则和合并同类项法则计算即可得出答案.
20．（2分）定义一种对正整数n的“F”运算：①当n为奇数时，结果为3n＋5；②当n为偶数时，结果为 (其中k是使 为奇数的正整数)，运算重复进行下去．例如：取n＝26，运算如图3－3－9所示．

图3－3－9
若n＝449，则第449次“F”运算的结果是　 　．
【答案】8
【完整解答】解：本题提供的“F运算”，需要对正整数n分情况(奇数、偶数)循环计算，由于n=449为奇数应先进行F①运算，
即3×449+5=1352(偶数)，
需再进行F②运算，
即1352÷23=169(奇数)，
再进行F①运算，得到3×169+5=512(偶数)，
再进行F②运算，即512÷29=1(奇数)，
再进行F①运算，得到3×1+5=8(偶数)，
再进行F②运算，即8÷23=1，
再进行F①运算，得到3×1+5=8(偶数)，…，
即第1次运算结果为1352，…，
第4次运算结果为1，第5次运算结果为8，…，
可以发现第6次运算结果为1，第7次运算结果为8，
从第6次运算结果开始循环，且奇数次运算的结果为8，偶数次为1，而第499次是奇数，
这样循环计算一直到第449次“F运算”，得到的结果为8.
故本题答案为：8.

【思路引导】解决此类问题的关键在于将新运算转化为学过的数的有关运算法则进行计算，通过计算可得出规律：可以发现第6次运算结果为1，第7次运算结果为8，从第6次运算结果开始循环，且奇数次运算的结果为8，偶数次为1，而第499次是奇数，可求解。
三．解答题（共11小题，满分64分）
21．（4分）（2022七上·巴中期末）先化简，再求值.已知代数式2（3x2﹣x+2y﹣xy）﹣3（2x2﹣3x﹣y+xy），其中x+y＝ ，xy＝﹣2.
【答案】解：


，
当x+y＝ ，xy＝﹣2时，原式
【思路引导】首先根据去括号法则、合并同类项法则对原式进行化简，然后将已知条件代入进行计算.
22．（6分）（2022七上·宝安期末）
（1）（3分）化简：-2（x2+2xy-1）-（x2+4xy）
（2）（3分）先化简，再求值：3（a2+ab2）-（ab+3ab2），其中a=2，b=
【答案】（1）原式= -2x2-4xy+2-x2-4xy= -3x2-8xy+2；
（2）原式= 3a2+3ab2-ab-3ab2= 3a2-ab，
当a=2，b=- 时，
原式=3×22-2×（- ）=13.
【思路引导】（1）先去括号，再合并同类项，即可得出答案；
（2）先去括号，再合并同类项，把原式进行化简，再把a，b的值代入进行计算，即可得出答案.
23．（5分）（2022七上·汇川期末）化简并求值：－5（a2－2ab＋b2）＋4（2a2－3ab＋3b2）＋2ab，其中a＝－1， .
【答案】解：－5（a2－2ab＋b2）＋4（2a2－3ab＋3b2）＋2ab
=
=
=
当a＝－1， 时，原式=
【思路引导】先去括号（括号前是负号，去掉括号和负号，括号里的每一项都要变号；括号前面是正号，去掉括号和正号，括号里的每一项都不变号，括号前的数要与括号里的每一项都要相乘），再合并同类项对原式进行化简，然后将a、b的值代入化简后的式子中进行计算即可.
24．（5分）（2021七上·岚皋期末）在数轴上点A表示数a，点B表示数b，点C表示数c，并且a是多项式的二次项系数，b是绝对值最小的数，c是单项式的次数.请直接写出a、b、c的值并在数轴上把点A，B，C表示出来.

【答案】解：∵a是多项式的二次项系数，
∴a=-1，
∵b是绝对值最小的数，
∴b=0，
∵c是单项式的次数.
∴c=2+1=3，
将各数在数轴上表示如下：

【思路引导】根据多项式与单项式的次数的概念可得a=-1，c=3，由b是绝对值最小的数可得b=0，将各数在数轴上表示出来即可.
25．（5分）（2021七上·遂宁期末）已知：关于x、 的多项式 与多项式 的差的值与字母x的取值无关，求代数式 的值.
【答案】解： - =（1-b）x2+（a+3）x-7y+3+b
由于与字母x的取值无关所以1-b=0 ，a+3=0得b=1，a=-3
原式=-a2-7ab-4b2
当b=1，a=-3时
原式=-9+21-4=8
【思路引导】根据整式的加减法法则可得(x2+ax-y+b)-(bx2-3x+6y-3)=(1-b)x2+(a+3)x-7y+3+b，根据题意可得1-b=0，a+3=0，求出a、b的值，利用去括号法则以及合并同类项法则对待求式进行化简，然后将a、b的值代入计算即可.
26．（5分）（2021七上·陇县期末）已知关于x，y的式子的值与字母x的取值无关，求式子的值.
【答案】解：原式
，
由题可得，多项式的值与字母x无关，
，
解得，


，
代入，可得：，
故代数式的值为：.
【思路引导】先去括号，再合并同类项将第一个代数式化简，再根据此式子的值与x无关，可得到含x2和x项的系数为0，可得到关于n，m的方程组，解方程组求出m，n的值，然后将第二个代数式去括号并合并同类项化简，最后将m，n的值代入代数式求值.
27．（5分）（2022七上·黔西南期末）先化简，再求值： ，其中a，b满足 和 是同类项.
【答案】解：原式
.
因为 和 是同类项，
所以 ，
解得 ，
所以原式
【思路引导】首先根据去括号法则以及合并同类项法则对原式进行化简，根据同类项的概念可得3a=6，1=b+2，求出a、b的值，然后代入化简后的式子中进行计算.
28．（7分）（2021七上·澄海期末）某同学在黑板上符合题意解答了一道整式的计算题，但被另一位同学不慎擦掉了算式中的一部分，如图所示：
．
（1）（3分）求被擦掉的多项式；
（2）（4分）若，求被擦掉多项式的值．
【答案】（1）解：设被擦掉的多项式为M，
则

．
（2）解：若，
则

．
【思路引导】（1）根据题意列出算式，再利用整式的加减法计算即可；
（2）将x的值代入（1）中的代数式计算即可。
29．（7分）（2021七上·巢湖期末）现在有一种既隔热又耐老化的新型窗框材料——“断桥铝”，下图是这种材料做成的两种长方形窗框，已知窗框的长都是米，宽都是米．

（1）（3分）若一用户需Ⅰ型的窗框2个，Ⅱ型的窗框3个，求共需这种材料多少米（接缝忽略不计）？
（2）（4分）已知＞，求一个Ⅰ型的窗框比一个Ⅱ型的窗框节约这种材料多少米？
【答案】（1）解：根据图形，1个Ⅰ型窗框用料（）米；
1个Ⅱ型窗框用料（）米；
2个Ⅰ型窗框和3个Ⅱ型窗框共需这种材料（单位：米）


；
（2）解：1个Ⅱ型窗框和1个Ⅰ型窗框多用这种材料（单位：米）


．
【思路引导】（1）根据题意列出算式，去掉括号合并即可；
（2）用1个Ⅱ型窗框用料-1个Ⅰ型窗框用料，列出算式，去掉括号合并即可。
30．（5分）（2019七上·海曙期中）如图，它是由A、B、E、F四个正方形，C、D两个长方形拼成的大长方形，已知正方形F的边长为6，求拼成的大长方形周长．

【答案】【解答】 解：设A正方形边长为a，E正方形边长为x ，则正方形F的边长为a+x，正方形B的边长为a+x+a=2a+x, 于是大长方形的长为B、F的边长之和，为2a+x+a+x=3a+2x；
大长方形的宽为E和F的正方形边长之和，为x+a+x=2x+a, 则大长方形周长为2×(3a+2x+2x+a)=
8x+8a；
∵a+x=6，所以8x+8a=8(a+x)=48.
【思路引导】设A正方形边长为a，E正方形边长为x ，先把正方形F的边长和正方形B的边长用含a和x的代数式表示，于是大长方形的长和宽可用含a和x的代数式表示，则大长方形的周长可以用代数式表示出来，结合正方形F的边长为6，于是可求大长方形的周长.
31．（10分）（2021七上·揭西期末）七年级学习代数式求值时，遇到这样一类题“代数式的值与的取值无关，求的值”，通常的解题方法是：把x、y看作字母，a看作系数合并同类项，因为代数式的值与x的取值无关，所以含项的系数为0，
即原式＝，所以，则 ．

（1）（3分）若关于的多项式的值与的取值无关，求值；
（2）（3分）已知A，B；且3A＋6B的值与无关，求的值；
（3）（4分）7张如图1的小长方形，长为a，宽为b，按照图2方式不重叠地放在大长方形ABCD内，大长方形中未被覆盖的两个部分（图中阴影部分），设右上角的面积为，左下角的面积为，当AB的长变化时，的值始终保持不变，求与的等量关系．
【答案】（1）解：
，
关于的多项式的值与的取值无关，
，
解得．
（2）解：，



，
的值与无关，
，
解得．
（3）解：设，
由图可知，，，
则

，
当的长变化时，的值始终保持不变，
的值与的值无关，
，
．
【思路引导】（1）由题可知代数式的值与x的取值无关，所以含项的系数为0， 故将多项式进行整理，令x的系数为0，即可求出m；
（2）根据整式混合运算法则化简3A+6B可得（15y-6)x-9， 根据其值与无关 得出15y-6=0，解之即可；
（3）设AB=x， 由图可知，， ，即可得S1-S2 的代数式，根据取值与x无关可得a-2b=0，即a=2b.