广东省深圳市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类(含答案)

这是一份广东省深圳市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类(含答案)，共31页。试卷主要包含了探究，发现，，绘制成扇形统计图等内容，欢迎下载使用。

广东省深圳市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类
一．实数的运算（共1小题）
1．（2023•深圳）计算：（1+π）0+2﹣|﹣3|+2sin45°．
二．二元一次方程组的应用（共1小题）
2．（2023•深圳）某商场在世博会上购置A，B两种玩具，其中B玩具的单价比A玩具的单价贵25元，且购置2个B玩具与1个A玩具共花费200元．
（1）求A，B玩具的单价；
（2）若该商场要求购置B玩具的数量是A玩具数量的2倍，且购置玩具的总额不高于20000元，则该商场最多可以购置多少个A玩具？
三．反比例函数综合题（共1小题）
3．（2021•深圳）探究：是否存在一个新矩形，使其周长和面积为原矩形的2倍、倍、k倍．
（1）若该矩形为正方形，是否存在一个正方形，使其周长和面积都为边长为2的正方形的2倍？　 　（填“存在”或“不存在”）．
（2）继续探究，是否存在一个矩形，使其周长和面积都为长为3，宽为2的矩形的2倍？
同学们有以下思路：
①设新矩形长和宽为x、y，则依题意x+y＝10，xy＝12，联立得x2﹣10x+12＝0，再探究根的情况；
根据此方法，请你探究是否存在一个矩形，使其周长和面积都为原矩形的倍；
②如图也可用反比例函数与一次函数证明l1：y＝﹣x+10，l2：y＝，那么，
a．是否存在一个新矩形为原矩形周长和面积的2倍？　 　．
b．请探究是否有一新矩形周长和面积为原矩形的，若不存在，用图象表达；
c．请直接写出当结论成立时k的取值范围：　 　．

四．二次函数综合题（共1小题）
4．（2023•深圳）蔬菜大棚是一种具有出色的保温性能的框架覆膜结构，它出现使得人们可以吃到反季节蔬菜．一般蔬菜大棚使用竹结构或者钢结构的骨架，上面覆上一层或多层保温塑料膜，这样就形成了一个温室空间．
如图1，某个温室大棚的横截面可以看作矩形ABCD和抛物线AED构成，其中AB＝3m，BC＝4m，取BC中点O，过点O作线段BC的垂直平分线OE交抛物线AED于点E，若以O点为原点，BC所在直线为x轴，OE为y轴建立如图所示平面直角坐标系．
请回答下列问题：
（1）如图2，抛物线AED的顶点E（0，4），求抛物线的解析式；
（2）如图3，为了保证蔬菜大棚的通风性，该大棚要安装两个正方形孔的排气装置LFGT，SMNR，若FL＝NR＝0.75m，求两个正方形装置的间距GM的长；
（3）如图4，在某一时刻，太阳光线透过A点恰好照射到C点，此时大棚截面的阴影为CK，求CK的长．

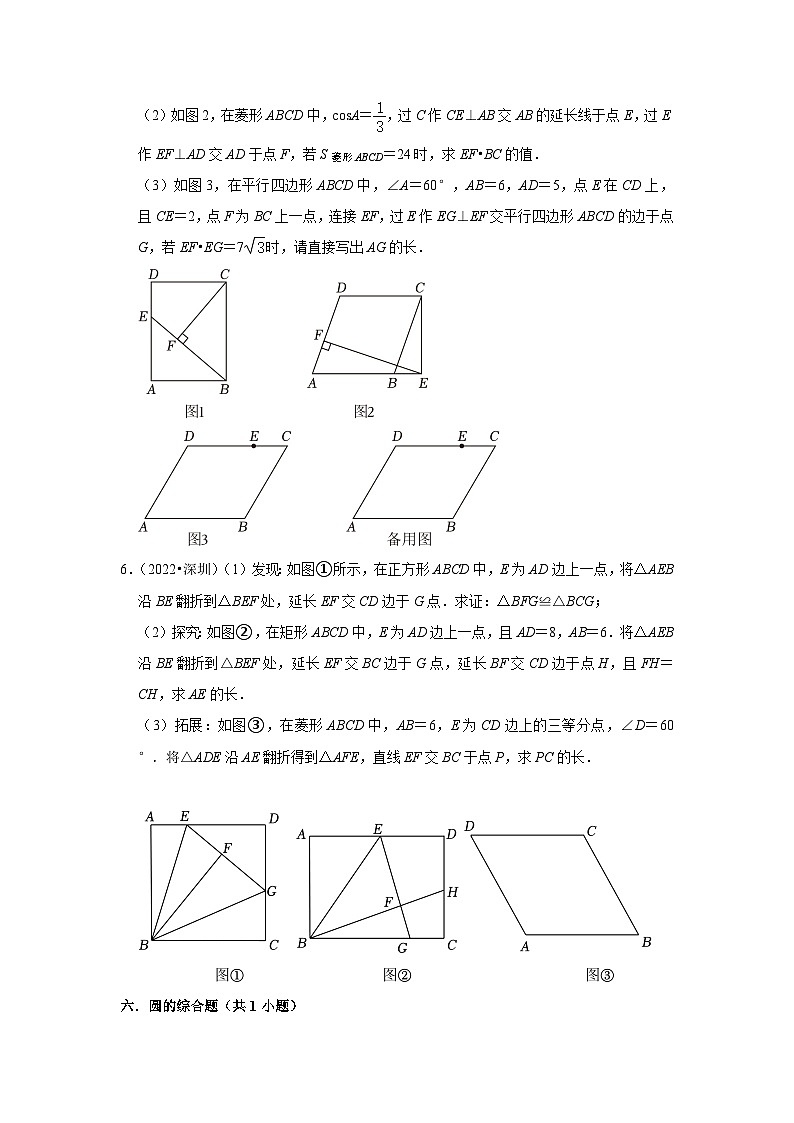
五．四边形综合题（共2小题）
5．（2023•深圳）（1）如图1，在矩形ABCD中，E为AD边上一点，连接BE，
①若BE＝BC，过C作CF⊥BE交BE于点F，求证：△ABE≌△FCB；
②若S矩形ABCD＝20时，则BE•CF＝　 　．
（2）如图2，在菱形ABCD中，cosA＝，过C作CE⊥AB交AB的延长线于点E，过E作EF⊥AD交AD于点F，若S菱形ABCD＝24时，求EF•BC的值．
（3）如图3，在平行四边形ABCD中，∠A＝60°，AB＝6，AD＝5，点E在CD上，且CE＝2，点F为BC上一点，连接EF，过E作EG⊥EF交平行四边形ABCD的边于点G，若EF•EG＝7时，请直接写出AG的长．

6．（2022•深圳）（1）发现：如图①所示，在正方形ABCD中，E为AD边上一点，将△AEB沿BE翻折到△BEF处，延长EF交CD边于G点．求证：△BFG≌△BCG；
（2）探究：如图②，在矩形ABCD中，E为AD边上一点，且AD＝8，AB＝6．将△AEB沿BE翻折到△BEF处，延长EF交BC边于G点，延长BF交CD边于点H，且FH＝CH，求AE的长．
（3）拓展：如图③，在菱形ABCD中，AB＝6，E为CD边上的三等分点，∠D＝60°．将△ADE沿AE翻折得到△AFE，直线EF交BC于点P，求PC的长．


六．圆的综合题（共1小题）
7．（2022•深圳）一个玻璃球体近似半圆O，AB为直径．半圆O上点C处有个吊灯EF，EF∥AB，CO⊥AB，EF的中点为D，OA＝4．
（1）如图①，CM为一条拉线，M在OB上，OM＝1.6，DF＝0.8，求CD的长度．
（2）如图②，一个玻璃镜与圆O相切，H为切点，M为OB上一点，MH为入射光线，NH为反射光线，∠OHM＝∠OHN＝45°，tan∠COH＝，求ON的长度．
（3）如图③，M是线段OB上的动点，MH为入射光线，∠HOM＝50°，HN为反射光线并与半圆O交于点N，在M从O运动到B的过程中，求N点的运动路径长．

七．作图—应用与设计作图（共1小题）
8．（2023•深圳）如图，在单位长度为1的网格中，点O，A，B均在格点上，OA＝3，AB＝2，以O为圆心，OA为半径画圆，请按下列步骤完成作图，并回答问题：
①过点A作切线AC，且AC＝4（点C在A的上方）；
②连接OC，交⊙O于点D；
③连接BD，与AC交于点E．
（1）求证：DB为⊙O的切线；
（2）求AE的长度．

八．相似形综合题（共1小题）
9．（2021•深圳）在正方形ABCD中，等腰直角△AEF，∠AFE＝90°，连接CE，H为CE中点，连接BH、BF、HF，发现和∠HBF为定值．
（1）①＝　 　；
②∠HBF＝　 　；
③小明为了证明①②，连接AC交BD于O，连接OH，证明了和的关系，请你按他的思路证明①②．
（2）小明又用三个相似三角形（两个大三角形全等）摆出如图2，＝k，∠BDA＝∠EAF＝θ（0°＜θ＜90°）．
求①＝　 　；（用k的代数式表示）
②＝　 　．（用k、θ的代数式表示）

九．频数（率）分布折线图（共1小题）
10．（2021•深圳）随机调查某城市30天空气质量指数（AQI），绘制成扇形统计图．
空气质量等级
空气质量指数（AQI）
频数
优
AQI≤50
m
良
50＜AQI≤100
15
中
100＜AQI≤150
9
差
AQI＞150
n
（1）m＝　 　，n＝　 　；
（2）求良的占比；
（3）求差的圆心角；
（4）统计表是一个月内的空气污染指数统计，然后根据这一个月内的统计进行估测一年的空气污染指数为中的天数，从统计表中可以得到空气污染指数为中的有9天．
根据统计表可知，一个月（30天）中有 　 　天AQI为中，估测该城市一年（以360天计）中大约有 　 　天AQI为中．

一十．列表法与树状图法（共1小题）
11．（2022•深圳）某工厂进行厂长选拔，从中抽出一部分人进行筛选，其中有“优秀”，“良好”，“合格”，“不合格”．

（1）本次抽查总人数为 　 　，“合格”人数的百分比为 　 　；
（2）补全条形统计图；
（3）扇形统计图中“不合格人数”的度数为 　 　；
（4）在“优秀”中有甲乙丙三人，现从中抽出两人，则刚好抽中甲乙两人的概率为 　 　．

广东省深圳市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类
参考答案与试题解析
一．实数的运算（共1小题）
1．（2023•深圳）计算：（1+π）0+2﹣|﹣3|+2sin45°．
【答案】．
【解答】解：（1+π）0+2﹣|﹣3|+2sin45°
＝1+2﹣3+2×
＝0+
＝．
二．二元一次方程组的应用（共1小题）
2．（2023•深圳）某商场在世博会上购置A，B两种玩具，其中B玩具的单价比A玩具的单价贵25元，且购置2个B玩具与1个A玩具共花费200元．
（1）求A，B玩具的单价；
（2）若该商场要求购置B玩具的数量是A玩具数量的2倍，且购置玩具的总额不高于20000元，则该商场最多可以购置多少个A玩具？
【答案】（1）A玩具的进价为50元，每件B玩具的进价为75元；（2）100个．
【解答】解：（1）设每件A玩具的进价为x元，则每件B玩具的进价为（x+25）元，
根据题意得：2（x+25）+x＝200，
解得：x＝50，
可得x+25＝50+25＝75，
则每件A玩具的进价为50元，每件B玩具的进价为75元；
（2）设商场可以购置A玩具y个，
根据题意得：50y+75×2y≤20000，
解得：y≤100，
则最多可以购置A玩具100个．
三．反比例函数综合题（共1小题）
3．（2021•深圳）探究：是否存在一个新矩形，使其周长和面积为原矩形的2倍、倍、k倍．
（1）若该矩形为正方形，是否存在一个正方形，使其周长和面积都为边长为2的正方形的2倍？　不存在　（填“存在”或“不存在”）．
（2）继续探究，是否存在一个矩形，使其周长和面积都为长为3，宽为2的矩形的2倍？
同学们有以下思路：
①设新矩形长和宽为x、y，则依题意x+y＝10，xy＝12，联立得x2﹣10x+12＝0，再探究根的情况；
根据此方法，请你探究是否存在一个矩形，使其周长和面积都为原矩形的倍；
②如图也可用反比例函数与一次函数证明l1：y＝﹣x+10，l2：y＝，那么，
a．是否存在一个新矩形为原矩形周长和面积的2倍？　存在　．
b．请探究是否有一新矩形周长和面积为原矩形的，若不存在，用图象表达；
c．请直接写出当结论成立时k的取值范围：　k≥　．

【答案】见试题解答内容
【解答】解：（1）由题意得，给定正方形的周长为8，面积为4，
若存在新正方形满足条件，则新正方形的周长为16，面积为8，
对应的边长为：4和，不符合题意，
∴不存在新正方形的周长和面积是边长为2的正方形的2倍．
故答案为：不存在．
（2）①设新矩形长和宽为x、y，则依题意x+y＝2.5，xy＝3，
联立，得：2x2﹣5x+6＝0，
∴Δ＝（﹣5）2﹣4×2×6＝﹣23＜0，
∴此方程无解，
∴不存在新矩形使得其周长和面积为原矩形的倍．
②a：从图象看来，函数y＝﹣x+10和函数y＝图象在第一象限有两个交点，
∴存在新矩形，使得周长和面积是原矩形的2倍．
故答案为：存在．
b：设新矩形长和宽为x、y，则依题意x+y＝2.5，xy＝3，
联立，得：2x2﹣5x+6＝0，
∴Δ＝（﹣5）2﹣4×2×6＝﹣23＜0，
∴此方程无解，
∴不存在新矩形使得其周长和面积为原矩形的倍．
从图象看来，函数y＝﹣x+2.5和函数y＝图象在第一象限没有交点，
∴不存在新矩形，使得周长和面积是原矩形的倍．
c：设新矩形长和宽为x、y，则依题意x+y＝5k，xy＝6k，
联立，得：x2﹣5kx+6k＝0，
∴Δ＝（﹣5k）2﹣4×1×6k＝25k2﹣24k，
设方程的两根为x1，x2，
当Δ≥0即25k2﹣24k≥0时，x1+x2＝5k＞0，x1x2＝6k＞0，
解得：k≥或k≤0（舍），
∴k≥时，存在新矩形的周长和面积均为原矩形的k倍．
故答案为：k≥．

四．二次函数综合题（共1小题）
4．（2023•深圳）蔬菜大棚是一种具有出色的保温性能的框架覆膜结构，它出现使得人们可以吃到反季节蔬菜．一般蔬菜大棚使用竹结构或者钢结构的骨架，上面覆上一层或多层保温塑料膜，这样就形成了一个温室空间．
如图1，某个温室大棚的横截面可以看作矩形ABCD和抛物线AED构成，其中AB＝3m，BC＝4m，取BC中点O，过点O作线段BC的垂直平分线OE交抛物线AED于点E，若以O点为原点，BC所在直线为x轴，OE为y轴建立如图所示平面直角坐标系．
请回答下列问题：
（1）如图2，抛物线AED的顶点E（0，4），求抛物线的解析式；
（2）如图3，为了保证蔬菜大棚的通风性，该大棚要安装两个正方形孔的排气装置LFGT，SMNR，若FL＝NR＝0.75m，求两个正方形装置的间距GM的长；
（3）如图4，在某一时刻，太阳光线透过A点恰好照射到C点，此时大棚截面的阴影为CK，求CK的长．

【答案】（1）抛物线表达式为．
（2）两个正方形装置的间距GM的长为．
（3）CK的长为．
【解答】解：（1）∵AB＝4，AD＝3，E（0，4），
∴A（﹣2，3），B（2，0），C（2，0），D（2，3），
设抛物线表达式为y＝ax2+bx+c，
将A、D、E三点坐标代入表达式，
得，
解得．
∴抛物线表达式为．
答：抛物线表达式为．
（2）设G（﹣t，3），则L（﹣t﹣），
∴，
解得（负值舍去），
∴GM＝2t＝．
答：两个正方形装置的间距GM的长为．
（3）取最右侧光线与抛物线切点为F，

设直线AC的解析式为y＝kx+b，
∴，
解得，
∴直线AC的解析式为y＝﹣x+，
∵FK∥AC，
设，
∴，
得，
∴，
解得m＝，
∴直线FK的解析式为，
令y＝0，得x＝，
∴．
∴CK＝BK﹣BC＝＝
答：CK的长为．
五．四边形综合题（共2小题）
5．（2023•深圳）（1）如图1，在矩形ABCD中，E为AD边上一点，连接BE，
①若BE＝BC，过C作CF⊥BE交BE于点F，求证：△ABE≌△FCB；
②若S矩形ABCD＝20时，则BE•CF＝　20　．
（2）如图2，在菱形ABCD中，cosA＝，过C作CE⊥AB交AB的延长线于点E，过E作EF⊥AD交AD于点F，若S菱形ABCD＝24时，求EF•BC的值．
（3）如图3，在平行四边形ABCD中，∠A＝60°，AB＝6，AD＝5，点E在CD上，且CE＝2，点F为BC上一点，连接EF，过E作EG⊥EF交平行四边形ABCD的边于点G，若EF•EG＝7时，请直接写出AG的长．

【答案】答案：
（1）①见解析；
②20；
（2）32；
（3）3 或4或 ．
【解答】解：（1）①∵四边形ABCD是矩形，则∠A＝∠ABC＝90°，
∴∠ABE+∠CBF＝90°，
又∵CF⊥BC，
∴∠FCB+∠CBF＝90°，∠CFB＝∠A＝90°，
∴∠FCB＝∠ABE，
又∵BC＝BE，
∴△ABE≌△FCB（AAS）；
②由①可得∠FCB＝∠ABE，∠CFB＝∠A＝90°，
∴△ABE∽△FCB．
∴＝，
又∵S矩形ABCD＝AB•CD＝20，
∴BE•CF＝AB•BC＝20，
（2）∵在菱形ABCD中，，
∴AD∥BC，AB＝BC，则∠CBE＝∠A，
∵CE⊥AB，∠CEB＝90°，
∴，
∴，
1∴，
∵EF⊥AD，CE⊥AB，
∴∠AFE＝∠BEC＝90°，
又∵∠CBE＝∠A，
∴△AFE∽△BEC，
∴，
∴EF•BC＝AE•CE＝AB×CE＝S菱形ABCD＝×24＝32；
（3）①当点G在AD边上时，如图所示，延长FE交AD的延长线于点M，连接GF，过点E作 EH⊥DM于点H，

∵平行四边形ABCD中，AB＝6，CE＝2，
∴CD＝AB＝6，
DE＝DC﹣EC＝6﹣2＝4，
∵DM∥FC，
∴△EDM∽△ECF，
∴，
＝＝2，
∴S△MGE＝2S△EFG＝EF•EG＝7，
在Rt△DEH 中，∠HDE＝∠A＝60°，
则 ，，
1∴，
∴MG＝7，
∵GE⊥EF，EH⊥MG，∠MEH＝90°﹣∠HEG＝∠HGE，
∴tan∠MEH＝tan∠HGE，
∵，
∴HE2＝HM•HG，
设AG＝a，则GD＝AD﹣AG＝5﹣a，
GH＝GD+HD＝5﹣a+2＝7﹣a，HM＝GM﹣GH＝7﹣（7﹣a）＝a，
，
解得：a＝3或a＝4，
即AG＝3或 AG＝4，
②当G点在AB边上时，如图所示，

连接GF，延长GE交BC的延长线于点M，过点G作GN∥AD，则GN∥BC，四边形ADNG是平行四边形，
设AG＝x，则 DN＝AG＝x，EN＝DE﹣DN＝4﹣x，
∵GN∥CM，
∴△ENG∽△ECM，
∴，
∴，
∴，
∵EF•，
∴，
过点E作EH⊥BC于点H，
在Rt△EHC中，EC＝2，∠ECH＝60°，
∴，CH＝1，
∴，
则 ，
∴，
∴，，
∵∠MEF＝∠EHM＝90°，∠FEH＝90°﹣∠MEH＝∠M，
∴tan∠FEH＝tan∠M，
即 ，
∴EH2＝FH•HM，
即 ，
解得：x2＝8 （舍去），
即 ；
③当G点在BC边上时，如图所示，

过点B作BT⊥DC于点T，
在Rt△BTC 中，，
，
，
EF•EG＝7，
∴，
∵，
∴G点不可能在BC边上，综上所述，AG的长为3或4或 ．
6．（2022•深圳）（1）发现：如图①所示，在正方形ABCD中，E为AD边上一点，将△AEB沿BE翻折到△BEF处，延长EF交CD边于G点．求证：△BFG≌△BCG；
（2）探究：如图②，在矩形ABCD中，E为AD边上一点，且AD＝8，AB＝6．将△AEB沿BE翻折到△BEF处，延长EF交BC边于G点，延长BF交CD边于点H，且FH＝CH，求AE的长．
（3）拓展：如图③，在菱形ABCD中，AB＝6，E为CD边上的三等分点，∠D＝60°．将△ADE沿AE翻折得到△AFE，直线EF交BC于点P，求PC的长．


【答案】（1）证明见解答过程；
（2）AE的长为；
（3）CP的长为或．
【解答】（1）证明：∵将△AEB沿BE翻折到△BEF处，四边形ABCD是正方形，
∴AB＝BF，∠BFE＝∠A＝90°，
∴∠BFG＝90°＝∠C，
∵AB＝BC＝BF，BG＝BG，
∴Rt△BFG≌Rt△BCG（HL）；
（2）解：延长BH，AD交于Q，如图：

设FH＝HC＝x，
在Rt△BCH中，BC2+CH2＝BH2，
∴82+x2＝（6+x）2，
解得x＝，
∴DH＝DC﹣HC＝，
∵∠BFG＝∠BCH＝90°，∠HBC＝∠FBG，
∴△BFG∽△BCH，
∴＝＝，即＝＝，
∴BG＝，FG＝，
∵EQ∥GB，DQ∥CB，
∴△EFQ∽△GFB，△DHQ∽△CHB，
∴＝，即＝，
∴DQ＝，
设AE＝EF＝m，则DE＝8﹣m，
∴EQ＝DE+DQ＝8﹣m+＝﹣m，
∵△EFQ∽△GFB，
∴＝，即＝，
解得m＝，
∴AE的长为；
方法2：连接GH，如图：

∵CH＝FH，GH＝GH，
∴Rt△FGH≌Rt△CGH（HL），
∴CG＝FG，
设CG＝FG＝x，则BG＝8﹣x，
在Rt△BFG中，BF2+FG2＝BG2，
∴62+x2＝（8﹣x）2，
解得x＝，
∴BG＝BC﹣x＝，
∵∠GBE＝∠AEB＝∠FEB，
∴EG＝BG＝，
∴EF＝EG﹣FG＝；
∴AE＝；
（3）解：方法一：
（Ⅰ）当DE＝DC＝2时，延长FE交AD于Q，过Q作QH⊥CD于H，如图：

设DQ＝x，QE＝y，则AQ＝6﹣x，
∵CP∥DQ，
∴△CPE∽△QDE，
∴＝＝2，
∴CP＝2x，
∵△ADE沿AE翻折得到△AFE，
∴EF＝DE＝2，AF＝AD＝6，∠QAE＝∠FAE，
∴AE是△AQF的角平分线，
∴＝，即＝①，
∵∠D＝60°，
∴DH＝DQ＝x，HE＝DE﹣DH＝2﹣x，HQ＝DH＝x，
在Rt△HQE中，HE2+HQ2＝EQ2，
∴（2﹣x）2+（x）2＝y2②，
联立①②可解得x＝，
∴CP＝2x＝；
（Ⅱ）当CE＝DC＝2时，延长FE交AD延长线于Q'，过Q'作Q'H'⊥CD交CD延长线于H'，如图：

设DQ'＝x'，Q'E＝y'，则AQ'＝6+x'，
同理∠Q'AE＝∠EAF，
∴＝，即＝，
由H'Q'2+H'E2＝Q'E2得：（x'）2+（x'+4）2＝y'2，
可解得x'＝，
∴CP＝x'＝，
综上所述，CP的长为或．
方法二：
（Ⅰ）当DE＝DC＝2时，连接CF，过P作PK⊥CD于K，如图：

∵四边形ABCD是菱形，∠D＝60°，
∴△ABC，△ADC是等边三角形，
∴∠ACB＝∠ACD＝60°，AD＝AC，
∴∠PCK＝60°，
∵将△ADE沿AE翻折得到△AFE，
∴∠AFE＝∠D＝60°＝∠ACB，AF＝AD＝AC，EF＝DE＝2，
∴∠AFC＝∠ACF，
∴∠PFC＝∠PCF，
∴PF＝PC，
设PF＝PC＝2m，
在Rt△PCK中，CK＝m，PK＝m，
∴EK＝EC﹣CK＝4﹣m，
在Rt△PEK中，EK2+PK2＝PE2，
∴（4﹣m）2+（m）2＝（2+2m）2，
解得m＝，
∴PC＝2m＝；
（Ⅱ）当CE＝DC＝2时，连接CF，过P作PT⊥CD交DC延长线于T，如图：

同（Ⅰ）可证AC＝AD＝AF，∠ACB＝60°＝∠D＝∠AFE，
∴∠ACF＝∠AFC，
∴∠ACF﹣∠ACB＝∠AFC﹣∠AFE，即∠PCF＝∠PFC，
∴PC＝PF，
设PC＝PF＝2n，
在Rt△PCT中，
CT＝n，PT＝n，
∴ET＝CE+CT＝2+n，EP＝EF﹣PF＝DE﹣PF＝4﹣2n，
在Rt△PET中，PT2+ET2＝PE2，
∴（n）2+（2+n）2＝（4﹣2n）2，
解得n＝，
∴PC＝2n＝，
综上所述，CP的长为或．
六．圆的综合题（共1小题）
7．（2022•深圳）一个玻璃球体近似半圆O，AB为直径．半圆O上点C处有个吊灯EF，EF∥AB，CO⊥AB，EF的中点为D，OA＝4．
（1）如图①，CM为一条拉线，M在OB上，OM＝1.6，DF＝0.8，求CD的长度．
（2）如图②，一个玻璃镜与圆O相切，H为切点，M为OB上一点，MH为入射光线，NH为反射光线，∠OHM＝∠OHN＝45°，tan∠COH＝，求ON的长度．
（3）如图③，M是线段OB上的动点，MH为入射光线，∠HOM＝50°，HN为反射光线并与半圆O交于点N，在M从O运动到B的过程中，求N点的运动路径长．

【答案】（1）2；（2）；（3）4+π．
【解答】解：（1）∵OM＝1.6，DF＝0.8，EF∥AB，
∴DF是△COM的中位线，
∴点D是OC的中点，
∵OC＝OA＝4，
∴CD＝2；
（2）如图②，过点N作ND⊥OH于点D，

∵∠OHN＝45°，
∴△NHD是等腰直角三角形，
∴ND＝HD，
∵tan∠COH＝，∠NDO＝90°，
∴＝，
设ND＝3x＝HD，则OD＝4x，
∵OH＝OA＝4，
∴OH＝3x+4x＝4，
∴x＝，
∴ND＝×3＝，OD＝×4＝，
∴ON＝＝；
（3）如图，当点M与点O重合时，点N也与点O重合，当点M运动至点B时，点N运动至点T，故点N的运动路径长为OA+的长，

∵∠HOM＝50°，OH＝OB，
∴∠OHB＝∠OBH＝65°，
∵∠OHM＝∠OHT，OH＝OT，
∴∠OTH＝∠OHT＝65°，
∴∠TOH＝50°，
∴∠AOT＝180°﹣50°﹣50°＝80°，
∴的长＝＝π，
∴点N的运动路径长＝4+π．
七．作图—应用与设计作图（共1小题）
8．（2023•深圳）如图，在单位长度为1的网格中，点O，A，B均在格点上，OA＝3，AB＝2，以O为圆心，OA为半径画圆，请按下列步骤完成作图，并回答问题：
①过点A作切线AC，且AC＝4（点C在A的上方）；
②连接OC，交⊙O于点D；
③连接BD，与AC交于点E．
（1）求证：DB为⊙O的切线；
（2）求AE的长度．

【答案】（1）见解答；
（2）1.5．
【解答】解：如图：

（1）∵AC是圆的切线，
∴∠OAC＝90°，
∴AC＝5，
由题意得：OD＝AO＝3，OB＝OC＝5，∠AOC＝∠DOB，
∴△AOC≌△DOB（SAS），
∴∠ODB＝∠OAC＝90°，
∵OD是圆的半径，
∴DB为⊙O的切线；
（2）∵∠CDE＝∠CAO＝90°，∠C＝∠C，
∴△CDE∽△CAO，
∴，
即：，
解得：CE＝2.5，
∴AE＝AC﹣CE＝4﹣2.5＝1.5．
八．相似形综合题（共1小题）
9．（2021•深圳）在正方形ABCD中，等腰直角△AEF，∠AFE＝90°，连接CE，H为CE中点，连接BH、BF、HF，发现和∠HBF为定值．
（1）①＝　　；
②∠HBF＝　45°　；
③小明为了证明①②，连接AC交BD于O，连接OH，证明了和的关系，请你按他的思路证明①②．
（2）小明又用三个相似三角形（两个大三角形全等）摆出如图2，＝k，∠BDA＝∠EAF＝θ（0°＜θ＜90°）．
求①＝　　；（用k的代数式表示）
②＝　　．（用k、θ的代数式表示）

【答案】（1）①；②45°；③见解答过程；（2）①；②．
【解答】解：①；②45°；
③由正方形的性质得：，O为AC的中点，
又∵H为CE的中点，
∴OH∥AE，OH＝，
∵△AEF是等腰直角三角形，
∴AE＝，
∴，
∵OH∥AE，
∴∠COH＝∠CAE，
∴∠BOH＝∠BAF，
∴△BOH∽△BAF，
∴，
∴∠HBF＝∠HBO+∠DBF＝∠DBA＝45°；
（2）①如图2，连接AC交BD于点O，连接OH，

由（1）中③问同理可证：△DOH∽△DAF，
∴，
②由①知：△DOH∽△DAF，
∴∠HDO＝∠FDA，
∴∠HDF＝∠BDA＝θ，
在△HDF中，，
设DF＝2t，HD＝kt，
作HM⊥DF于M，
∴HM＝DH×sinθ＝ktsinθ，DM＝ktcosθ，
∴MF＝DF﹣DM＝（2﹣kcosθ）t，
在Rt△HMF中，由勾股定理得：
HF＝，
∴．
九．频数（率）分布折线图（共1小题）
10．（2021•深圳）随机调查某城市30天空气质量指数（AQI），绘制成扇形统计图．
空气质量等级
空气质量指数（AQI）
频数
优
AQI≤50
m
良
50＜AQI≤100
15
中
100＜AQI≤150
9
差
AQI＞150
n
（1）m＝　4　，n＝　2　；
（2）求良的占比；
（3）求差的圆心角；
（4）统计表是一个月内的空气污染指数统计，然后根据这一个月内的统计进行估测一年的空气污染指数为中的天数，从统计表中可以得到空气污染指数为中的有9天．
根据统计表可知，一个月（30天）中有 　9　天AQI为中，估测该城市一年（以360天计）中大约有 　108　天AQI为中．

【答案】（1）4，2；
（2）50%；
（3）24°；
（4）9，108．
【解答】解：（1）根据题意，得m＝×30＝4，
所以n＝30﹣4﹣15﹣9＝2，
故答案为：4，2；
（2）良的占比＝×100%＝50%；
（3）差的圆心角＝×360°＝24°；
（4）根据折线图，一个月（30天）中有9天AQI为中，估测该城市一年（以360天计）中大约有360×＝108（天）AQI为中．
故答案为：9，108．
一十．列表法与树状图法（共1小题）
11．（2022•深圳）某工厂进行厂长选拔，从中抽出一部分人进行筛选，其中有“优秀”，“良好”，“合格”，“不合格”．

（1）本次抽查总人数为 　50人　，“合格”人数的百分比为 　40%　；
（2）补全条形统计图；
（3）扇形统计图中“不合格人数”的度数为 　115.2°　；
（4）在“优秀”中有甲乙丙三人，现从中抽出两人，则刚好抽中甲乙两人的概率为 　　．
【答案】见试题解答内容
【解答】解：（1）本次抽查的总人数为8÷16%＝50（人），
“合格”人数的百分比为1﹣（32%+16%+12%）＝40%，
故答案为：50人，40%；
（2）补全图形如下：

（3）扇形统计图中“不合格”人数的度数为360°×32%＝115.2°，
故答案为：115.2°；
（4）列表如下：

甲
乙
丙
甲

（乙，甲）
（丙，甲）
乙
（甲，乙）

（丙，乙）
丙
（甲，丙）
（乙，丙）

由表知，共有6种等可能结果，其中刚好抽中甲乙两人的有2种结果，
所以刚好抽中甲乙两人的概率为＝．
故答案为：．