中职高教版（2021）5.3 实系数一元二次方程的解法教案

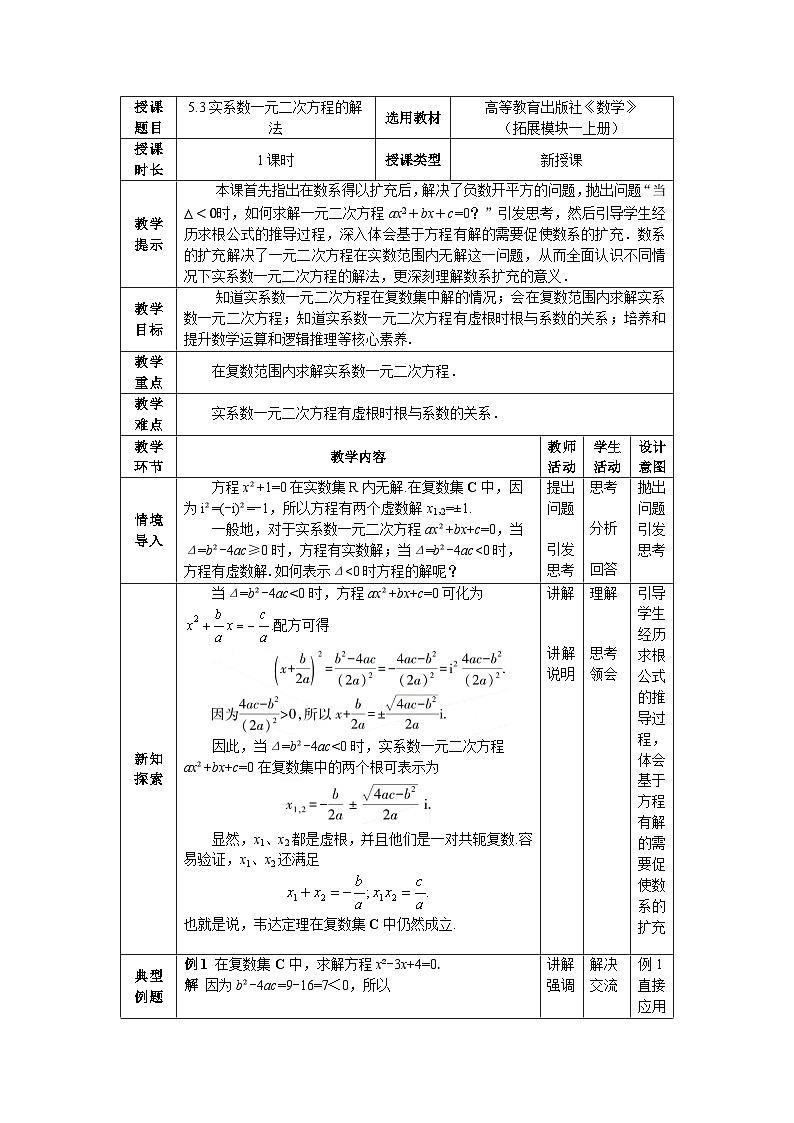
授课题目

5.3实系数一元二次方程的解法

选用教材

高等教育出版社《数学》

（拓展模块一上册）

授课时长

1课时

授课类型

新授课

教学提示

本课首先指出在数系得以扩充后，解决了负数开平方的问题，抛出问题“当时，如何求解一元二次方程ax2＋bx＋c=0？”引发思考，然后引导学生经历求根公式的推导过程，深入体会基于方程有解的需要促使数系的扩充．数系的扩充解决了一元二次方程在实数范围内无解这一问题，从而全面认识不同情况下实系数一元二次方程的解法，更深刻理解数系扩充的意义．

教学目标

知道实系数一元二次方程在复数集中解的情况；会在复数范围内求解实系数一元二次方程；知道实系数一元二次方程有虚根时根与系数的关系；培养和提升数学运算和逻辑推理等核心素养.

教学重点

在复数范围内求解实系数一元二次方程．

教学难点

实系数一元二次方程有虚根时根与系数的关系．

教学环节

教学内容

教师

活动

学生

活动

设计

意图

情境导入

方程 x²+1=0 在实数集R内无解.在复数集C中，因为i²=(-i)²=-1，所以方程有两个虚数解x1,2=±1.

一般地，对于实系数一元二次方程ax²+bx+c=0，当Δ=b²-4ac≥0时，方程有实数解；当Δ=b²-4ac<0时，方程有虚数解.如何表示Δ<0时方程的解呢？

提出

问题

引发

思考

思考

分析

回答

抛出问题引发思考

新知探索

当Δ=b²-4ac<0时，方程ax²+bx+c=0可化为

.配方可得

因此，当Δ=b²-4ac<0时，实系数一元二次方程

ax²+bx+c=0在复数集中的两个根可表示为

显然，x1、x2都是虚根，并且他们是一对共轭复数.容易验证，x1、x2还满足

也就是说，韦达定理在复数集C中仍然成立.

讲解

讲解说明

理解

思考

领会

引导学生经历求根公式的推导过程，体会基于方程有解的需要促使数系的扩充

典型

例题

例1 在复数集C中，求解方程x²-3x+4=0.

解 因为b²-4ac=9-16=7＜0，所以

例2  已知实系数一元二次方程x²+mx+n=0的一个根是

 1+2i，求 它的另一个根和m 、n的值.

解  因为实系数一元二次方程x²+mx+n=0的一个根是虚数 1+2i，所以判别式Δ<0.于是，方程有两个互为共轭复数的根，从而方程 的另一个根是 1-2i. 

由根与系数的关系可得

即        m=-(x1+x2)=-[(1+2i)+](1-2i)] =-2, 

n=x1x2 = (1+2i) (1-2i) = 5.

例3 在复数集中解方程x4-16=0.

解  原方程可化为(x²+4) (x²-4)=0，因此x²+4=0或x²-4=0.由x²+4=0得x1=2i，x2=-2i；

由x²-4=0得x3=2i，x4=-2.

所以原方程的根为x1=2i，x2=-2i，x3=2i，x4=-2.

温馨提示

在复数集C中，实系数一元二次方程ax²+bx+c=0的求根公式为

当Δ=b²-4ac≥0时，；

当Δ=b²-4ac<0时，.

讲解

强调

指导学习

讲解

强调

指导学习

解决

交流

主动

求解

解决

交流

主动

求解

例1直接应用

公式

例2另一种方法是将一个根代入方程整理后求解

例3注意强调解题步骤

巩固练习

练习5.3

1.在复数集中解方程x2=-9.

2.在复数集中解方程x2+4x+5=0.

3.已知实系数一元二次方程x²+bx+c=0的一个根是

3-4i，求另一个根和b、c的值.

提问

巡视

指导

思考

求解

交流

掌握学生情况查漏补缺

归纳总结

引导

提问

回忆

反思

培养

学生

总结

学习

过程

能力

布置作业

1.书面作业：完成课后习题和《学习指导与练习》；

2.查漏补缺：根据个人情况对课堂学习复习与回顾;

3.拓展作业：阅读教材扩展延伸内容.

说明

记录

继续探究

延伸学习