江苏省南京市玄武区三年(2020-2022)九年级上学期期末数学试题汇编

这是一份江苏省南京市玄武区三年(2020-2022)九年级上学期期末数学试题汇编，文件包含江苏省南京市玄武区三年2020-2022九年级上学期期末数学试题汇编-03解答题提升题知识点分类doc、江苏省南京市玄武区三年2020-2022九年级上学期期末数学试题汇编-02填空题知识点分类doc、江苏省南京市玄武区三年2020-2022九年级上学期期末数学试题汇编-01选择题知识点分类doc、江苏省南京市玄武区三年2020-2022九年级上学期期末数学试题汇编-03解答题基础题知识点分类doc等4份试卷配套教学资源，其中试卷共84页， 欢迎下载使用。
江苏省南京市玄武区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类
一．根的判别式（共2小题）
1．（2020秋•玄武区期末）关于x的方程x2﹣2x+m＝p2，无论实数p取何值，该方程总有两个不相等的实数根，则实数m的取值范围为　 　．
2．（2022秋•玄武区期末）关于x的方程x2﹣2x﹣1＝p（p为常数）有两个不相等的正根，则p的取值范围是 　 　．
二．根与系数的关系（共3小题）
3．（2020秋•玄武区期末）若x1，x2是方程x2﹣2x﹣1＝0的两个实数根，则x12+x22+2x1x2的值为　 　．
4．（2021秋•玄武区期末）一元二次方程x2﹣x﹣1＝0的两个实数根分别为x1，x2，则x1x2﹣x1﹣x2的值为 　 　．
5．（2022秋•玄武区期末）设x1，x2是方程x2+5x﹣2＝0的两个根，则+的值是 　 　．
三．由实际问题抽象出一元二次方程（共2小题）
6．（2021秋•玄武区期末）某种药品经过两次降价，由每盒80元调至64元，若设平均每次降价的百分率为x，则由题意可列方程为 　 　．
7．（2022秋•玄武区期末）某公司一月份的产值为200万元，二，三月份的产值总和为720万元，设公司每月产值的平均增长率为x，则可列方程为 　 　．
四．二次函数的性质（共2小题）
8．（2020秋•玄武区期末）已知二次函数y＝ax2+bx+c（a、b、c是常数，且a≠0），函数值y与自变量x的部分对应值如下表：
x
…
﹣1
0
1
2
3
4
…
y
…
10
y1
2
1
2
5
…
当y＜y1时，自变量x的取值范围是　 　．
9．（2021秋•玄武区期末）二次函数y＝2x2﹣4x+3m的图象的顶点在x轴上，则m的值为 　 　．
五．二次函数图象上点的坐标特征（共1小题）
10．（2021秋•玄武区期末）二次函数y＝x2﹣2的图象上横坐标与纵坐标相等的点的坐标为 　 　．
六．二次函数图象与几何变换（共1小题）
11．（2020秋•玄武区期末）在平面直角坐标系中，将函数y＝2x2的图象先向右平移2个单位长度，再向上平移3个单位长度后，所得图象的函数表达式为　 　．
七．勾股定理（共1小题）
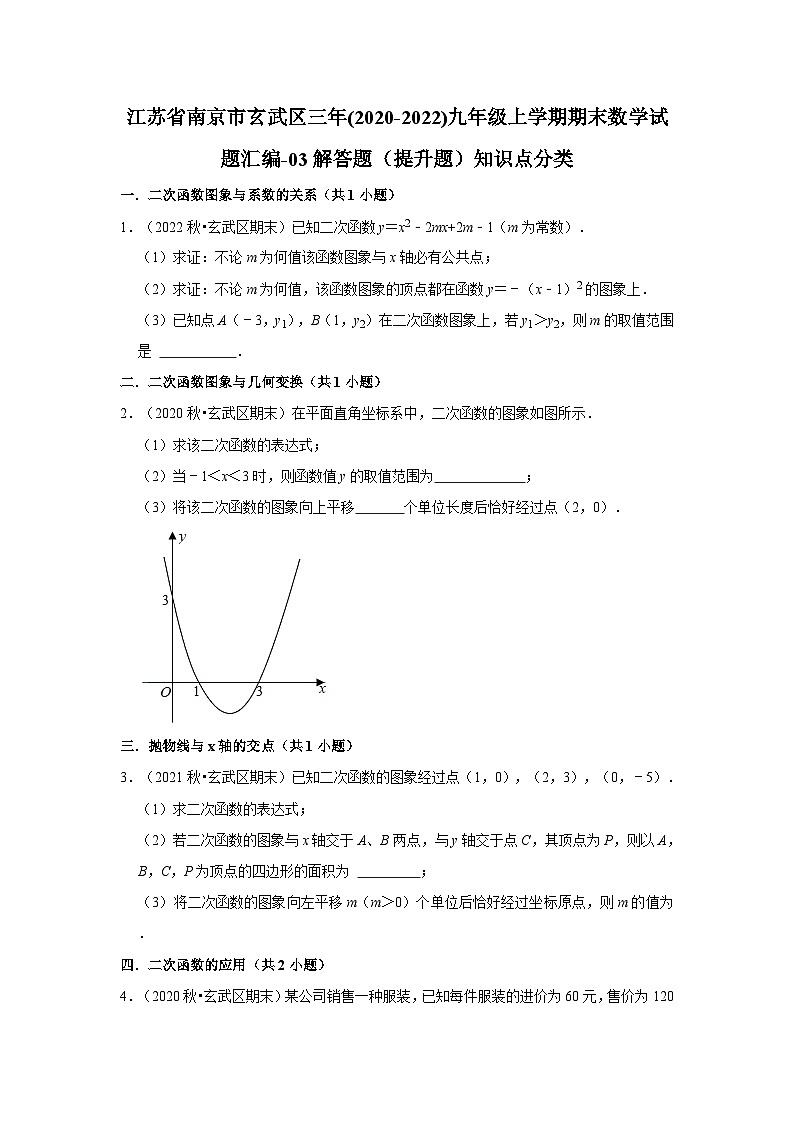
12．（2021秋•玄武区期末）如图，在△ABC中，∠ACB＝90°，AC＝，BC＝2，将△ABC绕点C按逆时针方向旋转得到△DEC，连接AD，BE，直线AD，BE相交于点F，连接CF，在旋转过程中，线段CF的最大值为 　 　．

八．菱形的性质（共1小题）
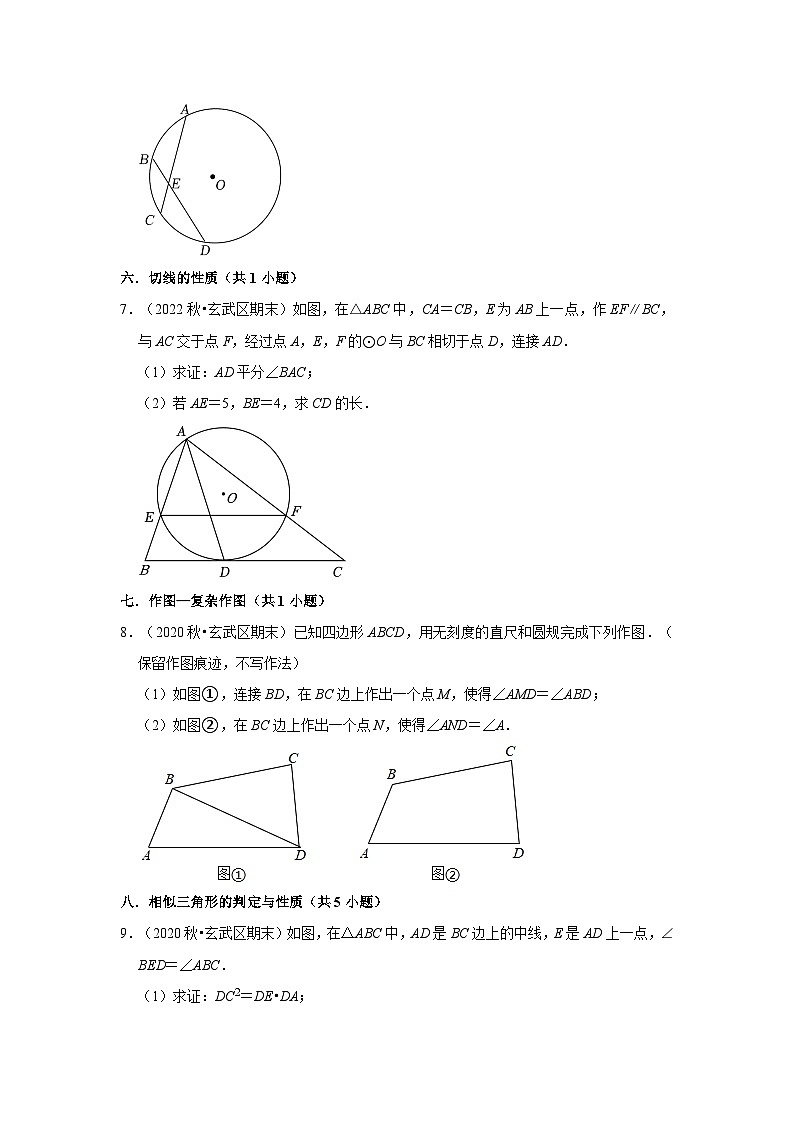
13．（2020秋•玄武区期末）如图，在菱形ABCD中，O是对角线BD上一点，⊙O经过点A，B，C，若⊙O的半径为2，OD＝4，则BC的长为　 　．

九．圆周角定理（共1小题）
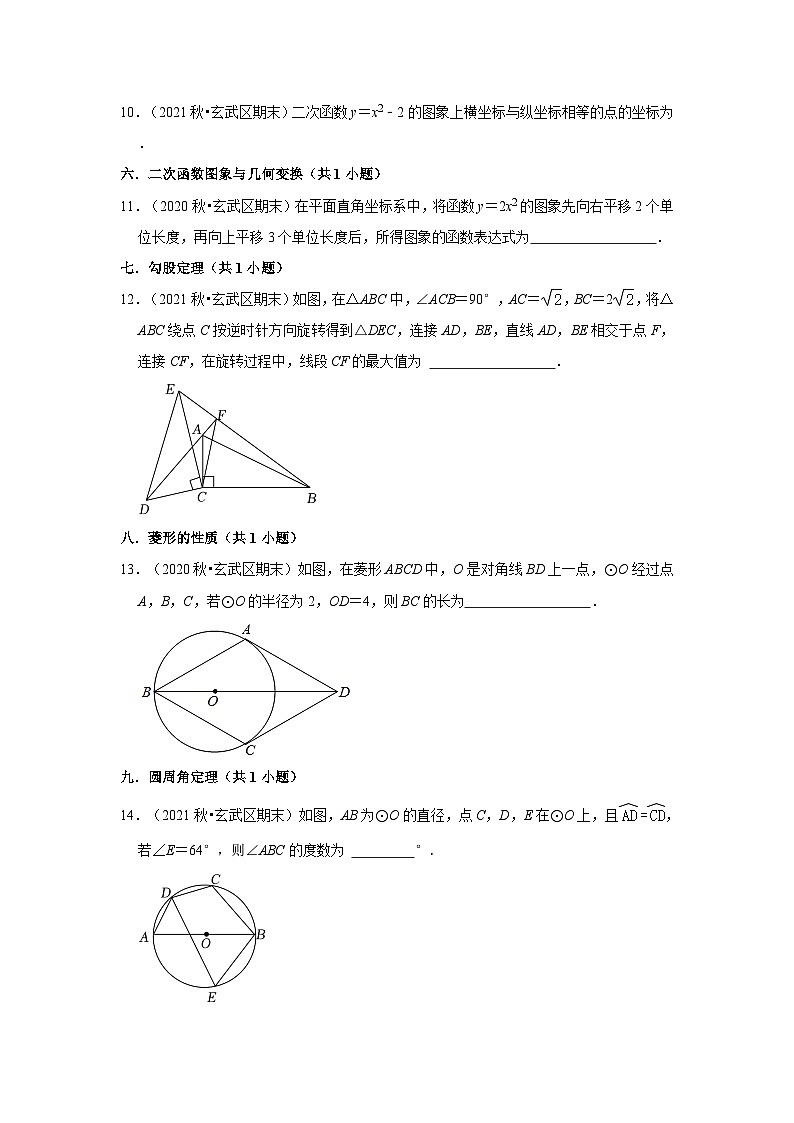
14．（2021秋•玄武区期末）如图，AB为⊙O的直径，点C，D，E在⊙O上，且，若∠E＝64°，则∠ABC的度数为 　 　°．

一十．三角形的外接圆与外心（共1小题）
15．（2020秋•玄武区期末）在△ABC中，AB＝AC＝10，BC＝12，M，N是BC边上两个动点，若AB，AC边上分别存在点P，Q使得∠MPN＝∠MQN＝60°，则线段MN的最小值为　 　．
一十一．切线的性质（共1小题）
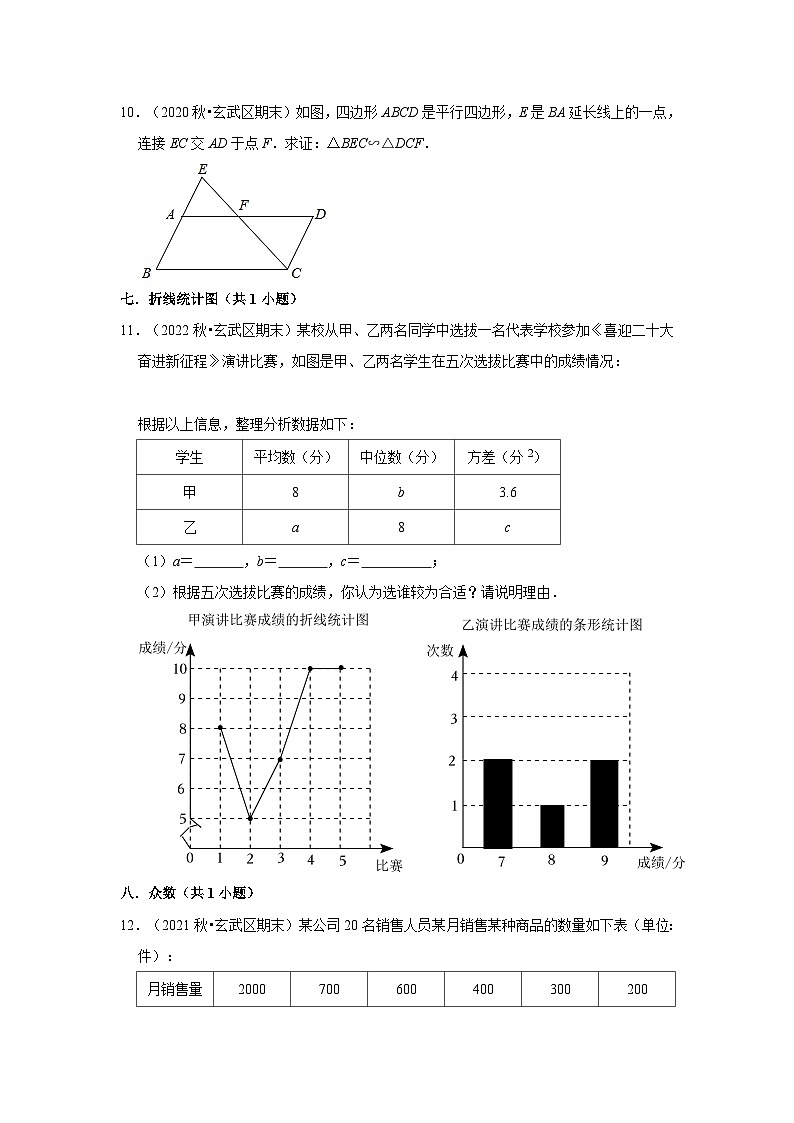
16．（2021秋•玄武区期末）如图，在矩形ABCD中，F是边AD上的点，经过A，B，F三点的⊙O与CD相切于点E．若AB＝6，FD＝2，则⊙O的半径是 　 　．

一十二．三角形的内切圆与内心（共1小题）
17．（2022秋•玄武区期末）Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，则它的内切圆半径是　 　．
一十三．正多边形和圆（共2小题）
18．（2021秋•玄武区期末）已知边长为2的正三角形，能将其完全覆盖的最小圆的面积为 　 　．
19．（2022秋•玄武区期末）如图，正五边形ABCDE内接于⊙O，AF是⊙O的直径，P是⊙O上的一点（不与点B，F重合），则∠BPF的度数为 　 　°．

一十四．圆锥的计算（共3小题）
20．（2020秋•玄武区期末）用一个半径为10cm半圆纸片围成一个圆锥的侧面（接缝忽略不计），则该圆锥的高为　 　．
21．（2021秋•玄武区期末）已知圆锥的母线长为4，其侧面展开图的圆心角的度数为90°，则圆锥的底面圆的半径为 　 　．
22．（2022秋•玄武区期末）用一个圆心角为150°，半径为12的扇形作一个圆锥的侧面，则这个圆锥的底面半径为 　 　．
一十五．比例的性质（共2小题）
23．（2020秋•玄武区期末）若，则＝　 　．
24．（2022秋•玄武区期末）已知，则＝　 　．
一十六．黄金分割（共1小题）
25．（2022秋•玄武区期末）已知B是线段AC的黄金分割点，AB＞BC，若AC＝10，则AB＝　 　．（答案保留根号）
一十七．相似三角形的性质（共1小题）
26．（2021秋•玄武区期末）已知△ABC∽△DEF，且△ABC与△DEF的面积之比为1：2，当BC＝1cm，对应边EF的长是　 　．
一十八．相似三角形的判定与性质（共2小题）
27．（2020秋•玄武区期末）如图，在△ABC中，DE∥FG∥BC，△ADE的面积＝梯形DFGE的面积＝梯形FBCG的面积，则的值为　 　．

28．（2022秋•玄武区期末）如图，在▱ABCD中，以CD为直径作⊙O，⊙O经过点A，且与BD交于点E，连接AE并延长，与BC交于点F，若F是BC的中点，AF＝6，则AB＝　 　．

一十九．概率公式（共1小题）
29．（2022秋•玄武区期末）如图，转盘中有6个面积都相等的扇形，任意转动转盘1次，当转盘停止转动时，“指针所落扇形中的数为奇数”发生的概率为 　 　．

二十．几何概率（共1小题）
30．（2020秋•玄武区期末）如图，一个可以自由转动的圆形转盘被等分成6个相同的扇形区域，并涂上了相应的颜色，随机转动转盘，转盘停止时，指针恰好落在黄色区域的概率是　 　．


江苏省南京市玄武区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类
参考答案与试题解析
一．根的判别式（共2小题）
1．（2020秋•玄武区期末）关于x的方程x2﹣2x+m＝p2，无论实数p取何值，该方程总有两个不相等的实数根，则实数m的取值范围为　m＜1　．
【答案】m＜1．
【解答】解：∵x2﹣2x+m＝p2，
∴x2﹣2x+m﹣p2＝0，
∴Δ＝（﹣2）2﹣4×1×（m﹣p2）＝4﹣4m+4p2，
∵无论实数p取何值，该方程总有两个不相等的实数根，
∴4﹣4m+4p2＞0，
∵4p2＞0，
∴4﹣4m＞0，
∴m＜1，
故答案为：m＜1．
2．（2022秋•玄武区期末）关于x的方程x2﹣2x﹣1＝p（p为常数）有两个不相等的正根，则p的取值范围是 　﹣2＜p＜﹣1　．
【答案】﹣2＜p＜﹣1．
【解答】解：∵x2﹣2x﹣1＝p，
∴x2﹣2x﹣1﹣p＝0，
∵关于x的一元二次方程x2﹣2x﹣1﹣p＝0有两个不相等的正根，
∴Δ＝b2﹣4ac＝4﹣4（﹣p﹣1）＞0，且﹣1﹣p＞0，
解得：﹣2＜p＜﹣1．
故答案为：﹣2＜p＜﹣1．
二．根与系数的关系（共3小题）
3．（2020秋•玄武区期末）若x1，x2是方程x2﹣2x﹣1＝0的两个实数根，则x12+x22+2x1x2的值为　4　．
【答案】4．
【解答】解：∵x1，x2是方程x2﹣2x﹣1＝0的两个实数根，
∴x1+x2＝2，
∴x12+x22+2x1x2
＝（x1+x2）2
＝22
＝4，
故答案为：4．
4．（2021秋•玄武区期末）一元二次方程x2﹣x﹣1＝0的两个实数根分别为x1，x2，则x1x2﹣x1﹣x2的值为 　﹣2　．
【答案】﹣2．
【解答】解：∵一元二次方程x2﹣x﹣1＝0的两个实数根分别为x1，x2，
∴x1+x2＝1，x1•x2＝﹣1，
∴x1x2﹣x1﹣x2＝﹣1﹣1＝﹣2，
故答案为：﹣2．
5．（2022秋•玄武区期末）设x1，x2是方程x2+5x﹣2＝0的两个根，则+的值是 　29　．
【答案】29．
【解答】解：∵设x1，x2是方程x2+5x﹣2＝0的两个根，
∴，
∴
＝（﹣5）2﹣2×（﹣2）
＝25+4
＝29．
故答案为：29．
三．由实际问题抽象出一元二次方程（共2小题）
6．（2021秋•玄武区期末）某种药品经过两次降价，由每盒80元调至64元，若设平均每次降价的百分率为x，则由题意可列方程为 　80（1﹣x）2＝64　．
【答案】80（1﹣x）2＝64．
【解答】解：设平均每次降价的百分率是x，则第二次降价后的价格为80（1﹣x）2元，
根据题意得：80（1﹣x）2＝64，
故答案为：80（1﹣x）2＝64．
7．（2022秋•玄武区期末）某公司一月份的产值为200万元，二，三月份的产值总和为720万元，设公司每月产值的平均增长率为x，则可列方程为 　200（1+x）+200（1+x）2＝720　．
【答案】200（1+x）+200（1+x）2＝720．
【解答】解：由题意得：200（1+x）+200（1+x）2＝720；
故答案为：200（1+x）+200（1+x）2＝720．
四．二次函数的性质（共2小题）
8．（2020秋•玄武区期末）已知二次函数y＝ax2+bx+c（a、b、c是常数，且a≠0），函数值y与自变量x的部分对应值如下表：
x
…
﹣1
0
1
2
3
4
…
y
…
10
y1
2
1
2
5
…
当y＜y1时，自变量x的取值范围是　0＜x＜4　．
【答案】0＜x＜4．
【解答】解：由题意得，抛物线的顶点坐标为（2，1），对称轴是直线x＝2，开口向上，
∴当x＝0时的函数值与x＝4时的函数值相等，
∴当y＜y1时，自变量x的取值范围是0＜x＜4，
故答案为：0＜x＜4．
9．（2021秋•玄武区期末）二次函数y＝2x2﹣4x+3m的图象的顶点在x轴上，则m的值为 　　．
【答案】．
【解答】解：∵y＝2x2﹣4x+3m＝2（x﹣1）2﹣2+3m，
∴顶点（1，3m﹣2），
∵顶点在x轴上，
∴3m﹣2＝0，
∴m＝，
故答案为：．
五．二次函数图象上点的坐标特征（共1小题）
10．（2021秋•玄武区期末）二次函数y＝x2﹣2的图象上横坐标与纵坐标相等的点的坐标为 　（﹣1，﹣1）、（2，2）　．
【答案】（﹣1，﹣1）或（2，2）．
【解答】解：二次函数y＝x2﹣2的图象上，横坐标与纵坐标相等的点的坐标是（a，a），则a＝a2﹣2，即a2﹣a﹣2＝0，
解得a＝2或﹣1．
故符合条件的点的坐标是：（﹣1，﹣1）或（2，2）．
故答案为：（﹣1，﹣1）或（2，2）．
六．二次函数图象与几何变换（共1小题）
11．（2020秋•玄武区期末）在平面直角坐标系中，将函数y＝2x2的图象先向右平移2个单位长度，再向上平移3个单位长度后，所得图象的函数表达式为　y＝2（x﹣2）2+3　．
【答案】y＝2（x﹣2）2+3．
【解答】解：将函数y＝2x2的图象先向右平移2个单位长度得到y＝2（x﹣2）2，
再向上平移3个单位长度后，得到y＝2（x﹣2）2+3，
故答案为：y＝2（x﹣2）2+3．
七．勾股定理（共1小题）
12．（2021秋•玄武区期末）如图，在△ABC中，∠ACB＝90°，AC＝，BC＝2，将△ABC绕点C按逆时针方向旋转得到△DEC，连接AD，BE，直线AD，BE相交于点F，连接CF，在旋转过程中，线段CF的最大值为 　　．

【答案】．
【解答】解：如图，取AB的中点H，连接CH，FH，设EC，DF交于点G，

在△ABC中，∠ACB＝90°，
∵AC＝，BC＝2，
∴AB＝＝＝，
由旋转可知：△DCE≌△ACB，
∴∠DCE＝∠ACB，DC＝AC，CE＝CB，
∴∠DCA＝∠BCE，
∵∠ADC＝（180°﹣∠ACD）÷2，
∠BEC＝（180°﹣∠BCE）÷2，
∴∠ADC＝∠BEC，
∵∠DGC＝∠EGF，
∴∠DCG＝∠EFG＝90°，
∴∠AFB＝90°，
∵H是AB的中点，
∴FH＝AB，
∵∠ACB＝90°，
∴CH＝AB，
∴FH＝CH＝AB＝，
在△FCH中，FH+CH≥CF，
当F，C，H在一条直线上时，CF＝+＝．
∴线段CF的值为．
故答案为：．
八．菱形的性质（共1小题）
13．（2020秋•玄武区期末）如图，在菱形ABCD中，O是对角线BD上一点，⊙O经过点A，B，C，若⊙O的半径为2，OD＝4，则BC的长为　2　．

【答案】见试题解答内容
【解答】解：连接AC，AC交BD于E，连接OC，

∵⊙O的半径为2，OD＝4，
∴OB＝OC＝2，BD＝OB+OD＝2+4＝6，
∵四边形ABCD是菱形，
∴AB＝BC，AC⊥BC，BE＝DE，
∴BE＝DE＝3，∠BEC＝90°，
∴OE＝BE﹣OB＝3﹣2＝1，
在Rt△OEC中，由勾股定理得：CE＝＝＝，
在Rt△BEC中，由勾股定理得：BC＝＝＝2，
故答案为：．
九．圆周角定理（共1小题）
14．（2021秋•玄武区期末）如图，AB为⊙O的直径，点C，D，E在⊙O上，且，若∠E＝64°，则∠ABC的度数为 　52　°．

【答案】52．
【解答】解：连接BD，

∵∠E＝64°，
∴∠DAB＝∠E＝64°，
∵AB是⊙O的直径，
∴∠ADB＝90°，
∴∠ABD＝90°﹣∠DAB＝26°，
∵，
∴∠CBD＝∠ABD＝26°，
∴∠ABC＝∠ABD+∠CBD＝52°，
故答案为：52．
一十．三角形的外接圆与外心（共1小题）
15．（2020秋•玄武区期末）在△ABC中，AB＝AC＝10，BC＝12，M，N是BC边上两个动点，若AB，AC边上分别存在点P，Q使得∠MPN＝∠MQN＝60°，则线段MN的最小值为　　．
【答案】．
【解答】解：如图1，在BC边上取点M、N，以MN为边作等边三角形△MNG，并作△MNG外接圆⊙O，
则所对圆周角＝∠MGN＝60°，⊙O交AB、AC于P、Q时，易知∠MPN＝∠MQN＝60°，
则⊙O与△ABC有交点，且半径最小时MN可取得最小值，
∴⊙O与AB、AC相切时MN最小，如图2，
此时OP⊥AB，OP＝r，OQ⊥AC，OQ＝r，
∴圆心O在∠BAC角平分线上，
即在△ABC底边上的高AD上，
∴BD＝CD＝6，AD＝8，
连接MO，NO，PO，
圆心角∠MON＝2∠MPN＝120°，MO＝NO＝OP＝OQ，
∴∠MOD＝60°，
设半径为r，则，，
∵∠ADB＝∠APO＝90°，∠BAD＝∠BAD，
∴△APO∽△ADB，
∴，即，
解得，
则．
故答案为：．

一十一．切线的性质（共1小题）
16．（2021秋•玄武区期末）如图，在矩形ABCD中，F是边AD上的点，经过A，B，F三点的⊙O与CD相切于点E．若AB＝6，FD＝2，则⊙O的半径是 　　．

【答案】．
【解答】解：设BC与⊙O交于点H，
连接OE、OF、DH，
则FH∥DC，FH＝DC＝6，
∵⊙O与CD相切于点E，
∴OE⊥BC，
∴OE⊥FH，
∴FG＝3，
设⊙O的半径为r，则OG＝r﹣2，
在Rt△OFG中，OF2＝FG2+OG2，即r2＝（r﹣2）2+32，
解得：r＝，
故答案为：．

一十二．三角形的内切圆与内心（共1小题）
17．（2022秋•玄武区期末）Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，则它的内切圆半径是　2　．
【答案】见试题解答内容
【解答】解：如图，⊙O切AC于E，切BC于F，切AB于G，连OE，OF，
∴OE⊥AC，OF⊥BC，
∴四边形CEOF为正方形，
∵∠C＝90°，AC＝6，BC＝8，
∴AB＝10，
设⊙O的半径为r，则CE＝CF＝r，
∴AE＝AG＝6﹣r，BF＝BG＝8﹣r，
∴AB＝AG+BG＝AE+BF，即6﹣r+8﹣r＝10，
∴r＝2．
故答案为2．

一十三．正多边形和圆（共2小题）
18．（2021秋•玄武区期末）已知边长为2的正三角形，能将其完全覆盖的最小圆的面积为 　　．
【答案】．
【解答】解：连接OB、OC，过O作OD⊥BC于D，
∵△ABC是边长为4的等边三角形，BC＝2，
∴∠BOC＝120°，
∴∠BOD＝∠BOC＝60°，BD＝1，
∴OB＝＝，
∴能够完全覆盖这个正三角形的最小圆的面积为：π×（）2＝，
故答案为：．

19．（2022秋•玄武区期末）如图，正五边形ABCDE内接于⊙O，AF是⊙O的直径，P是⊙O上的一点（不与点B，F重合），则∠BPF的度数为 　54或126　°．

【答案】54或126．
【解答】解：连接OC，OD，
∵正五边形ABCDE的五个顶点把圆五等分，
∴＝，
∴∠AOC＝∠AOD，
∴∠COF＝∠DOF，
∵OC＝OD，
∴直径AF⊥CD，
∴＝，
∵∠COD＝×360°＝72°，
∴∠COF＝＝36°，
当P在上时，连接OB，BP，FP，
∵∠BOC＝×360°＝72°，
∴∠BOF＝∠BOC+∠COF＝108°，
∴，
当P在上时，
由圆内接四边形的性质得∠BPF＝180°﹣54°＝126°．
∴∠BPF的度数是54°或126°．
故答案为：54或126．

一十四．圆锥的计算（共3小题）
20．（2020秋•玄武区期末）用一个半径为10cm半圆纸片围成一个圆锥的侧面（接缝忽略不计），则该圆锥的高为　5cm　．
【答案】见试题解答内容
【解答】解：圆锥的侧面展开图的弧长为2π×10÷2＝10π（cm），
∴圆锥的底面半径为10π÷2π＝5（cm），
∴圆锥的高为：＝5（cm）．
故答案为：5cm．

21．（2021秋•玄武区期末）已知圆锥的母线长为4，其侧面展开图的圆心角的度数为90°，则圆锥的底面圆的半径为 　1　．
【答案】1．
【解答】解：设圆锥的底面圆的半径为r，
则2πr＝，
解得：r＝1，即圆锥的底面圆的半径为1，
故答案为：1．
22．（2022秋•玄武区期末）用一个圆心角为150°，半径为12的扇形作一个圆锥的侧面，则这个圆锥的底面半径为 　5　．
【答案】5．
【解答】解：扇形的弧长＝＝10π，
设圆锥的底面半径为R，则2πR＝10π，
所以R＝5．
故答案为：5；
一十五．比例的性质（共2小题）
23．（2020秋•玄武区期末）若，则＝　　．
【答案】见试题解答内容
【解答】解：∵，
∴＝＝，
∴＝．
故答案为：．
24．（2022秋•玄武区期末）已知，则＝　4　．
【答案】4．
【解答】解：∵，
∴设a＝3k，b＝5k，
∴＝＝＝4，
故答案为：4．
一十六．黄金分割（共1小题）
25．（2022秋•玄武区期末）已知B是线段AC的黄金分割点，AB＞BC，若AC＝10，则AB＝　5﹣5　．（答案保留根号）
【答案】5﹣5．
【解答】解：∵B是线段AC的黄金分割点，AB＞BC，AC＝10，
∴AB＝AC＝×10＝5﹣5，
故答案为：5﹣5．
一十七．相似三角形的性质（共1小题）
26．（2021秋•玄武区期末）已知△ABC∽△DEF，且△ABC与△DEF的面积之比为1：2，当BC＝1cm，对应边EF的长是　cm　．
【答案】cm．
【解答】解：∵△ABC∽△DEF，△ABC与△DEF的面积之比为1：2，
∴（BC：EF）2＝1：2，
解得BC：EF＝1：，
∵BC＝1cm，
∴EF＝cm．
故答案为：cm．
一十八．相似三角形的判定与性质（共2小题）
27．（2020秋•玄武区期末）如图，在△ABC中，DE∥FG∥BC，△ADE的面积＝梯形DFGE的面积＝梯形FBCG的面积，则的值为　　．

【答案】见试题解答内容
【解答】解：∵△ADE的面积＝梯形DFGE的面积＝梯形FBCG的面积，
∴＝，
∵DE∥BC，
∴△ADE∽△ABC，
∴＝＝，
故答案为：．
28．（2022秋•玄武区期末）如图，在▱ABCD中，以CD为直径作⊙O，⊙O经过点A，且与BD交于点E，连接AE并延长，与BC交于点F，若F是BC的中点，AF＝6，则AB＝　4　．

【答案】4，
【解答】解：连接AC，CE，
∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∵F是BC中点，
∴BF＝FC，
∵△BEF∽△DEA，
∴EF：EA＝BF：AD＝1：2，
∴EF＝AF＝×6＝2，
∵CD是⊙O的直径，
∴∠DEC＝∠DAC＝90°，
∴∠ACF＝∠DAC＝90°，∠BEC＝180°﹣∠DEC＝90°，
∴EF＝BF＝FC＝2，BC＝2EF＝4，
∵AC2＝AF2﹣FC2＝62﹣22＝32，
∴AB＝＝＝4．
故答案为：4．

一十九．概率公式（共1小题）
29．（2022秋•玄武区期末）如图，转盘中有6个面积都相等的扇形，任意转动转盘1次，当转盘停止转动时，“指针所落扇形中的数为奇数”发生的概率为 　　．

【答案】．
【解答】解：指针指向的可能情况有6种，而其中是奇数的有3种，
∴“指针所落扇形中的数为奇数”发生的概率为，
故答案为：．
二十．几何概率（共1小题）
30．（2020秋•玄武区期末）如图，一个可以自由转动的圆形转盘被等分成6个相同的扇形区域，并涂上了相应的颜色，随机转动转盘，转盘停止时，指针恰好落在黄色区域的概率是　　．

【答案】见试题解答内容
【解答】解：∵圆被等分成6份，其中黄色部分占2份，
∴指针指向黄色区域的概率是＝；
故答案为：．