




模型10 加权逆等线最值模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用)
展开
模型介绍
【模型总结】
R在求形如“QB+kPA”(k≠1)的式子最值问题时,关键是要通过相似三角形构造出与kPA相等的线段(即kPA=QC),将QB +kPA”型问题转化为“QB +QC”型将军饮马问题.当k=1时,加权逆等线就变成了逆等线拼接最值模型,此种情况属于权为1的特殊情况,只需通过全等三角形构造出相等线段即可,然后将问题变为常见的将军饮马问题求解即可.
R需要注意的是这里的QB、PA两条线段的延长线方向必须要有交叉,方能通过相似或全等三角形得到kPA的等线段.
【解题方法】
R利用比例线段构造相似三角形转化线段,把双动点问题转化为单动点将军饮马问题,利用“两点之间线段最短”从而解出答案.
例题精讲
考点一:直角三角形中的加权逆等线模型
【例1】.如图,已知BC⊥AB,BC=AB=3,E为BC边上一动点,连接AE,D点在AB延长线上,且CE=2BD,则AE+2CD的最小值为多少?
解:作CF⊥CB,且使得CF=6,连接EF
过点A做AG⊥CF,交FC延长线于点G
∵CFCB=CEBD=2 ,
∴△FCE∽△CBD,EF=2CD
∴AE+2CD=AE+EF
当A、E、F三点一线时,AE+EF取到最小值,此时AE+EF=AF
易知:四边形ABCG为正方形 AG=3,CG=3
FG=9 在Rt△FAG中,由勾股定理得 AF=310
AE+2CD的最小值为310
Ø变式训练
【变式1-1】.如图,等腰直角△ABC中,斜边BC=2,点D、E分别为线段A B和B C上的动点, ,求的最小值.
解:作BF⊥BC 并且使得BF=2,连接EF
∵BEAD=BFAC=22=2 ∴△BEF∽△ADC
∴EF=2 CD ∴AE+2CD=AE+EF
当A、E、F三点共线时,AE+EF取到最小值,此时AE+EF=AF
反向延长BF,过点A作AH⊥BF于点H
在Rt△AHF中,由勾股定理易得:AF=10
∴AE+2CD的最小值为10
【变式1-2】.如图, 在Rt△ABC中, AC=6,BC=8,∠ACB=90。,点E、F分别是A B 、B C边上的动点, 且, 求12CE+AF的最小值.
解:过点A作AD⊥AB,并且使得AD=12,连接DE,CD
过点C作CH⊥AB于点H,CG⊥AD延长线与点G
∵ADCF=AECF=2 ,∠DAE=∠ACF
∴△DAE∽△ACF ,DE=2AF, CE+2AF=CE+DE
当C、E、D三点共线时,取到最小值,此时CE+2AF=CE+DE=CD
由等面积法可得:CH=245 四边形AGCH为矩形, AG=CH=245 ,DG=AD+AG=845
在Rt△CAH中 由勾股定理得:AH=185
CG=AH=185
在Rt△DCG中, 由勾股定理得:CD=6205
12CE+AF=12(CE+2AF);12CE+AF的最小值为3205
考点二:特殊平行四边形中的加权逆等线模型
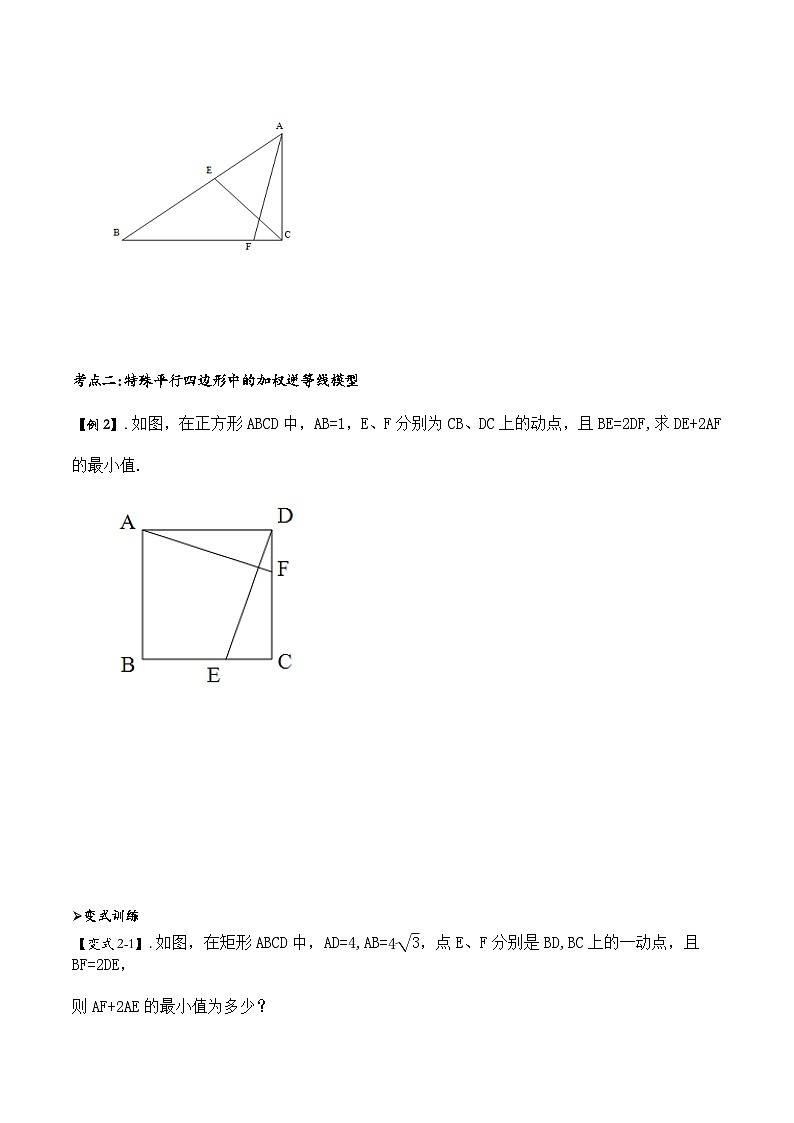
【例2】.如图,在正方形ABCD中,AB=1,E、F分别为CB、DC上的动点,且BE=2DF,求DE+2AF的最小值.
解:如图,延长BA至点,使得A=1;作点D
关于BC的对称点连接E,E 易知B=2
DE=E
∴E=2AF ∵DE=E ∴DE+2AF=E+E
当、E、 三点一线时,E+E取到最小值.
此时E+E=10 ∴ DE+2AF最小值为10
Ø变式训练
【变式2-1】.如图,在矩形ABCD中,AD=4,AB=43,点E、F分别是BD,BC上的一动点,且BF=2DE,则AF+2AE的最小值为多少?
解: 连接 D F, 延长D C至点 , 使 , 连接A G, 易证的最小值是 .
【变式2-2】.如图,在菱形ABCD中,∠BAD=120°,CD=4,M,N分别是边AB,AD的动点,满足AM=DN,连接CM、CN,E是边CM上的动点,F是CM上靠近C的四等分点,连接AE、BE、NF,当△CFN面积最小时,BE+AE的最小值为 .
解:如图,连接MN、AC,
∵四边形ABCD是菱形,∠BAD=120°,
∴AB=AD=CD,∠BAC=∠DAC=∠ADC=60°,
∴△ADC和△ABC为等边三角形,∴AC=DC,∠ACD=60°,
∵AM=DN,∴△AMC≌△DNC(SAS),
∴CM=CN,∠DCN=∠ACM,
∴∠MCN=∠MCA+∠ACN=∠DCN+∠ACN=∠ACD=60°,
∴△CMN为等边三角形,
∵点F是CM上靠近点C的四等分点,∴S△CFN=S△CMN,
∴△CMN的面积最小时,△CFN的面积也最小,
∵S△CMN=,
∴当CN和CM长度最短时,S△CMN的面积最小,即CN⊥AD,CM⊥AB时△CFN的面积最小,
取BE的中点为点G,连接MG,
∵△ABC为等边三角形,CM⊥AB,∴点M是AB的中点,
∴AE=BE,∴MG=AE=BE,∴BE+AE=AE+AE=AE,
∵点E是CM上的动点,∠AME=90°,∴AE的最小值即为AM的长度,
∵CD=4,∴AM=AB=2,∴(BE+AE)最小值=×2=3,故答案为:3.
实战演练
1.如图,等腰 ,D、E分别是 AB、BC边上的动点,且满足 , 求的最小值.
解:首先需要构建出,其次需要将AE和放到同一直线上.
如图所示,构建,且相似比为 ,则
此时 即最小值为M N;
如图所示,当A、 E 、F三点共线时,取得最小值为AF;
接下来,我们求解AF的长度.
∴CD的最小值为.
2.如图,M为矩形ABCD中AD边中点,E、F分别为BC、CD上的动点,且BE=2DF,若AB=1,BC=2,则ME+2AF的最小值为 .
方法一
解:如图,过点M作MH⊥BC于H.设DF=x,则BE=2x.
∵四边形ABCD是矩形,
∴∠BAD=∠B=∠D=90°,
∵MH⊥BC,
∴∠MHB=90°,
∴四边形ABHM是矩形,
∴AM=DM=BH=1,AB=MH=1,
∴EH=1﹣2x,
∴ME+2AF=+2=+,
欲求ME+2AF的最小值,相当于在x轴上找一点Q(2x,0),使得点Q到J(0,4),和K(1,1)的距离之和最小(如下图),
作点J关于x轴的对称点J′,连接KJ′交x轴于Q,连接JQ,此时JQ+QK的值最小,最小值=KJ′,
∵J′(0,﹣4),K(1,1),
∴KJ′==,
∴ME+2AF的最小值为, 故答案为.
方法二
延长AB至点G,使得BG=4,连接GE
作点G关于直线BC的对称点N,连接EN,MN
∴GE=NE
易证△BGE∽△DAF,∴GE=2AF
故 ME+2AF=ME+GE=ME+NE
当M 、E、 N三点共线时,ME+NE取到最小值
此时ME+NE=MN
在Rt△MNA中,由勾股定理可得:MN=26
3.如图,在正方形ABCD中,P为AD上一点,且APPD=21,E、F分别为CD、BC上的动点,且BF=3DE,若AD=3,求PF+3AE的最小值.
解:延长BA到点G,使得BG=3AD=9,作点G关于直线BC的对称点H
连接GF,FH,由对称原理可知:FH=GF
易证△GBF∽△ADE ∴GF=3AE 故PF+3AE=PF+GF=PF+FH
当P、F、H三点共线时,PF+FH取到最小值
此时PF+FH=PH
在Rt△ABP中,由勾股定理可得:PH=237
∴PF+3AE最小值为237
4.如图,在Rt△ACB,∠BCA=90°,∠A=30°,AC=,点D在线段AB上,点E在线段AB的延长线上,且BE=AD,则CE+CD的最小值是 .
解:如图所示,作点C关于AB的对称点G,连接CG,DG,AG,
则CD=GD,AC=AG,∠CAG=2∠CAB=60°,CG⊥AB,
∴△ACG是等边三角形,
∴CG=AC=,
如图,以DE,DG为边作平行四边形DEHG,则DG=EH,HG∥DE,
∴EH=CD,CG⊥GH,
∴CD+CE=HE+CE,
∴当C,E,H在同一直线上时,连接CH,CE+CD的最小值等于CH的长,
∵Rt△ACB中,∠BCA=90°,∠A=30°,AC=,
∴BC=tan30°×AC=1,AB=2BC=2,
∵DA=BE,
∴AB=DE=2,
∴平行四边形DEHG中,HG=2,
∴Rt△CGH中,CH===,
∴CE+CD的最小值等于,
故答案为:.
5.如图,在矩形ABCD中,AB=4,AD=6,点P在边AD上,点Q在边BC上,且AP=CQ,连接CP,QD,则PC+QD的最小值等于 10 .
解:如图,连接BP,
在矩形ABCD中,AD∥BC,AD=BC=6,
∵AP=CQ,
∴AD﹣AP=BC﹣CQ,
∴DP=QB,DP∥BQ,
∴四边形DPBQ是平行四边形,
∴PB∥DQ,PB=DQ,
则PC+QD=PC+PB,则PC+QD的最小值转化为PC+PB的最小值,
在BA的延长线上截取AE=AB=4,连接PE,
则BE=2AB=8,
∵PA⊥BE,
∴PA是BE的垂直平分线,
∴PB=PE,
∴PC+PB=PC+PE,
连接CE,则PC+QD=PC+PB=PC+PE≥CE,
∴CE===10,
∴PC+PB的最小值为10,
即PC+QD的最小值为10,
故答案为:10.
6.如图,平行四边形ABCD,AB>AD,AD=4,∠ADB=60°,点E、F为对角线BD上的动点,DE=2BF,连接AE、CF,则AE+2CF的最小值为 .
解:如图,在直线DB的上方作∠BDT=60°,且使得DT=2BC.过点T作TH⊥AD交AD的延长线于H.
∵四边形ABCD是平行四边形,
∴BC∥AD,AD=BC=4,
∴∠ADB=∠DBC=60°,
∴∠CBF=∠TDE,
∵BCDT=BFDE=12,
∴△CBF∽△TDE,
∴CFET=BCDT=12,
∴ET=2CF,
∵∠TDH=180°﹣60°﹣60°=60°,∠H=90°,DT=2BC=8,
∴DH=DT•cos60°=4,HT=3DH=43,
∴AH=AD+DH=8,
∴AT=AH2+HT2=82+(43)2=47,
∵AE+2CF=AE+ET,AE+ET≥AT,
∴AE+2CF≥47,
∴AE+2CF的最小值为47. 故答案为:47.
7.问题提出:
(1)如图①,在正方形ABCD中,E为边AB上一点(点E不与点A、B重合),连接DE,过点A作AF⊥DE,交BC于点F,则DE与AF的数量关系是:DE = AF;
问题探究:
(2)如图②,在矩形ABCD中,AB=4,AD=6,点E、F分别在边AB、CD上,点M为线段EF上一动点,过点M作EF的垂线分别交边AD、BC于点G、点H.若线段EF恰好平分矩形ABCD的面积,且DF=1,求GH的长;
问题解决:
(3)如图③,在正方形ABCD中,M为AD上一点,且,E、F分别为BC、CD上的动点,且BE=2DF,若AB=4,求ME+2AF的最小值.
解:(1)如图1,
DE=AF,理由如下:
在正方形ABCD中,
∠ABC=∠BAD=90°,AD=AB,∴∠BAF+∠AFB=90°,
∵AF⊥DE,
∴∠AOE=90°,∴∠BAF+∠AED=90°,∴∠AFB=∠AED,
∴△ABF≌△DAE(AAS),∴DE=AF,
故答案是“=”;
(2)如图2,
连接AC,交EF于O,
∵线段EF恰好平分矩形ABCD的面积,∴O是矩形的对称中心,∴BE=DF=1,
作DI∥EF,AJ∥GH,
∵四边形ABCD是矩形,∴DF∥IE,
∴四边形DIEF是平行四边形,∴EI=DF=1,∴AI=AB﹣BE﹣EI=2,
同理可得,
AJ=GH,
∵EF⊥GH,∴DI⊥AJ,
由(1)得,
∠AID=∠AJB,
∴△ADI∽△BAJ,∴=,∴=,∴BJ=,
在Rt△ABJ中由勾股定理得,
AJ===,∴GH=;
(3)如图3,
作EG⊥AD于G,∵,AD=4,∴AM=3,
设DF=a,则BE=2a,∴GM=AM﹣AG=3﹣2a,
在Rt△ADF中,AF==,
在Rt△EGM中,
ME==,
∴ME+2AF=+
=+
ME+2AF最小值可以看作在平面直角坐标系中,
点H(2a,0)到定点I(3,4),J(0,8)的距离之和最小,
如图4,
作J的对称点K,连接KI,
则KI与x轴的交点是H点,此时ME最小,
作IK⊥y轴于T,∴(ME+2AF)最小=KI===3.
8.如图,在△ABC中,∠ABC=60°,BC=6,AC=8,D、E分别为边AC、AB上两个动点.
(1)如图1,若D为AC中点,且DE平分△ABC的周长;
ⅰ)求AE﹣BE的值;
ⅱ)求证:∠AED=30°,并直接写出DE的值;
(2)如图2,若AE=CD,连接BD、CE,求BD+CE的最小值.
解:(1)ⅰ)∵AC=8,D为AC中点,∴AD=CD=4,
∵BC=6,DE平分△ABC的周长,∴AD+AE=CD+BC+BE,
∴4+AE=4+6+BE,∴AE﹣BE=6;
ⅱ)如图1,取AB的中点F,连接DF,
∵D为AC中点,∴DF∥BC,DF=BC=×6=3,∴∠AFD=∠B=60°,
∵∠AFD=∠AED+∠FDE,∠AED=30°,∴∠FDE=30°,
∴∠AED=∠FDE,∴EF=DF=3,
过F作FH⊥DE于H,∴FH=EF=,EH=DH,
∴EH==,∴DE=2EH=3;
(2)证明:过点C向上作CM∥AB,使CM=AC,连接BM,
过点M作MN⊥BC交BC的延长线于点N,
∵CM∥AB,∴∠A=∠ACM,
在△EAC和△DCM中,,
∴△EAC≌△DCM(SAS),∴CE=MD,
当点B,D,M三点在同一条直线上时,BD+MD的值最小为线段BM的长,
即BD+CE的最小值为BM的长,
∵CM∥AB,∴∠MCN=∠ABC=60°,
∵∠N=90°,CM=AC=8,∴∠CMN=30°,
∴CN=CM=4,∴MN=4,
∵BC=6,∴BN=BC+CN=6+4=10,
∴BM===2,∴BD+CE的最小值为2.
9.如图1,在▱ABCD中.AB=6.AC与BD交于点O,点E,F分别是线段AC,CD上的动点(点E,F不与A,C,D重合).AE=CF.设∠ACD=a,将线段AD绕点A按逆时针方向旋转a得到AP,连接PE,BE,BF.
(1)求证:△APE≌△CBF:
(2)如图2,若∠BOA=90°,∠ACD=40°,且点B、E、P在一条直线上,求BE+BF的值;
(3)当OB=OC,∠ACD=60°时,BE+BF长的最小值是 .
解:(1)∵∠ACD=∠PAD,∠DAC=∠ACB ∴∠PAE=∠BCF
∵AP=BC,AE=CF∴△APE≌△CBF(SAS)
(2)由(1)可知△APE≌△CBF
∴EP=BF ∴BP=BE+PF=BE+BF
∵∠BOA=90° ∴平行四边形ABCD为菱形 ∴AP=AD=AB
∵∠PAD=40° ∴∠PAB=120° ∴∠P=30°
如图,作AH⊥PB,垂足为H
在Rt△AHP中 AP=6 ∴HP=3 ∴BP=6 ∴BE+BF=6
(3)如图,PH垂直BA的延长线于H
∵OB=OC ∴▱ABCD为矩形
由(1)可知△APE≌△CBF ∴BE+BF的最小值即为BP长
在Rt△AHP中,AP=6,∠PAH=30° ∴HP=3,AH=9
在Rt△BHP中,BH=15,HP=3
∴BP==6 ∴BE+BF的最小值6
10.平行四边形ABCD中,N为线段CD上一动点.
(1)如图1,已知∠ADC<90°.若DR=BN,求证:四边形DRBN为平行四边形;
(2)如图2,已知∠ABC=60°.若BN为∠ABC的角平分线,T为线段BN上一点,DT的延长线交线段BC于点M,满足:tan∠BTM=且DN=BM.请认真思考(1)中图形,探究的值.
(3)如图3,平行四边形ABCD中,∠ABC=60°,AB=BC=2,P在线段BD上,Q在线段CD上,满足:BP=2CQ.直接写出(2QA+AP)的最小值为 2 .
(1)证明:如图1中,过点D作DE⊥BA交BA的延长线于E,过点B作BF⊥DC交DC的延长线于F.
∵四边形ABCD是平行四边形,
∴AD=BC,∠BAD=∠BCD,AB=CD, ∴∠DAE=∠BCF,
∵∠DEA=∠BFC=90°, ∴△ADE≌△CBF(AAS), ∴DE=BF,AE=CF,
∵DR=BN, ∴Rt△DER≌Rt△BFN(HL), ∴ER=FN, ∴AR=CN,
∵AB=CD, ∴BR=DN,
∵DR=BN, ∴四边形DRBN为平行四边形.
(2)解:如图2中,作DR∥BN交AB于R,连RM交BN于点P,
∵BR∥DN,RD∥BN,
∴四边形RBND是平行四边形, ∴BR=DN,
∵DN=BM, ∴BR=BM,
∵∠ABC=60°,BN为∠ABC的角平分线, ∴∠RBP=∠PBM=30°,
∴∠BPR=90°,
∵RD∥BN, ∴∠PRD=∠BPR=90°,
∵RD∥BN, ∴∠BTM=∠RDM,
∵tan∠BTM=, ∴tan∠RDM=,
设BM=a,则RM=a,
,
过点A作AK⊥RD于点K,
∵∠BRM=60°, ∴∠ARD=30°=∠ADR,
∴DK=RK=a, ∴AD===a,
在Rt△RDM中,RM2+RD2=MD2,
∴MD=a, ∴==.
(3)解:如图3中,连接AC,作CM∥BD,使得CM=AB,连接MQ,AM.
∵四边形ABCD是平行四边形,AB=BC=2,∠ABC=60°, ∴四边形ABCD是菱形,
∴△ABC,△ACD都是等边三角形,∠ABD=∠DBC=∠BDC=∠ABC=30°,
∴AC=AB=2,∠ACB=∠ACD=60°,
∵CM∥BD, ∴∠DCM=∠BDC=30°, ∴∠ABP=∠MCQ,
∵==2, ∴△ABP∽△MCQ, ∴==2, ∴QM=PA,
∴2QA+PA=2(AQ+AP)=2(AQ+QM),
∵AQ+QM≥AM,AM===,
∴AQ+QM的最小值为, ∴2AQ+PA的最小值为2. 故答案为:.
11.如图,在菱形ABCD中,∠BAD=120°,AB=6,连接BD.
(1)求BD的长;
(2)点E为线段BD上一动点(不与点B,D重合),点F在边AD上,且BE=DF.
①当CE⊥AB时,求四边形ABEF的面积;
②当四边形ABEF的面积取得最小值时,CE+CF的值是否也最小?如果是,求CE+CF的最小值;如果不是,请说明理由.
解:(1)过点D作DH⊥AB交BA的延长线于H,如图:
∵四边形ABCD是菱形, ∴AD=AB=6,
∵∠BAD=120°, ∴∠DAH=60°,
在Rt△ADH中, DH=AD•sin∠DAH=6×=3,
AH=AD•cos∠DAH=6×=3, ∴BD===6;
(2)①设CE⊥AB交AB于M点,过点F作FN⊥AB交BA的延长线于N,如图:
菱形ABCD中,
∵AB=BC=CD=AD=6,AD∥BC,∠BAD=120°, ∴∠ABC+∠BAD=180°,
∴∠ABC=180°﹣∠BAD=60°,
在Rt△BCM中,BM=BC•cos∠ABC=6×=3,
∵BD是菱形ABCD的对角线,
∴∠DBA=ABC=30°,
在Rt△BEM中,
ME=BM•tan∠DBM=3×=,
BE===2,
∵BE=DF, ∴DF=2, ∴AF=AD﹣DF=4,
在Rt△AFN中, ∠FAN=180°﹣∠BAD=60°, ∴FN=AF•sin∠FAN=4×=2,
AN=AF•cos∠FAN=4×=2,
∴MN=AB+AN﹣BM=6+2﹣3=5,
∴S四边形ABEF=S△BEM+S梯形EMNF﹣S△AFN
=EM•BM+(EM+FN)•MN﹣AN•FN
=3+(+2)×5﹣2×2
=+﹣2 =7;
②当四边形ABEF的面积取最小值时,CE+CF的值是最小,
理由:设DF=x,则BE=DF=x,过点C作CH⊥AB于点H,过点F作FG⊥CH于点G,
过点E作EY⊥CH于点Y,作EM⊥AB于M点,过点F作FN⊥AB交BA的延长线于N,如图:
∴EY∥FG∥AB,FN∥CH,
∴四边形EMHY、FNHG是矩形,
∴FN=GH,FG=NH,EY=MH,EM=YH,
由①可知:ME=BE=x,
BM=BE=x,
AN=AF=(AD﹣DF)=3﹣x,
FN=AF=,
CH=BC=3,BH=BC=3,
∴AM=AB﹣BM=6﹣x,
AH=AB﹣BH=3,
YH=ME=x,
GH=FN=,
EY=MH=BM﹣BH=x﹣3,
∴CY=CH﹣YH=3﹣x,
FG=NH=AN+AH=6﹣,CG=CH﹣GH=3﹣=x,
∴MN=AB+AN﹣BM=6+3﹣x﹣x=9﹣2x,
∴S四边形ABEF=S△BEM+S梯形EMNF﹣S△AFN
=EM•BM+(EM+FN)•MN﹣AN•FN
=x×x+(x+)•(9﹣2x)﹣(3﹣x)•
=x2﹣x+9
=(x﹣3)2+,
∵>0,
∴当x=3时,四边形ABEF的面积取得最小值,
方法一:CE+CF=+•
=+
=+×
=+×
=+,
∵(x﹣3)2≥0,当且仅当x=3时,(x﹣3)2=0,
∴CE+CF=+≥12,
当且仅当x=3时,CE+CF=12,即当x=3时,CE+CF的最小值为12,
∴当四边形ABEF的面积取最小值时,CE+CF的值也最小,最小值为12.
方法二:
如图:将△BCD绕点B逆时针旋转60°至△BAG,连接CG,
在Rt△BCG中,CG=2BC=12,
∵==,∠CDF=∠GBE=60°,
∴△BEG∽△DFC,
∴===,即GE=CF,
∴CE+CF=CE+GE≥CG=12,
即当且仅当点C、E、G三点共线时,CE+CF的值最小,
此时点E为菱形对角线的交点,BD中点,BE=3,DF=3,
∴当四边形ABEF的面积取最小值时,CE+CF的值也最小,最小值为12.
解法二:如图,在BD上截取DM,使得DM=2,在DA上取点F,连接DF,使得△DFM∽△BEC.
则有CE=FM,作点M关于AD阿德对称点M′,
∴CE+CF=FM+CF=(CF+FM)=(CF+FM′),
∴C,F,M′共线时,最小,
此时DF=3,可得CE+CF的值也最小,最小值为12.
模型24 辅助圆系列最值模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用): 这是一份模型24 辅助圆系列最值模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用),文件包含模型24辅助圆系列最值模型原卷版docx、模型24辅助圆系列最值模型解析版docx等2份试卷配套教学资源,其中试卷共53页, 欢迎下载使用。
模型48 梯子最值与斜边中点模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用): 这是一份模型48 梯子最值与斜边中点模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用),文件包含模型48梯子最值与斜边中点模型原卷版docx、模型48梯子最值与斜边中点模型解析版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
模型24 辅助圆系列最值模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用): 这是一份模型24 辅助圆系列最值模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用),文件包含模型24辅助圆系列最值模型原卷版docx、模型24辅助圆系列最值模型解析版docx等2份试卷配套教学资源,其中试卷共53页, 欢迎下载使用。












