【同步讲义】（人教A版2019）高中数学选修第三册：拓展一：近八年统计案例高考真题分类汇编 讲义

这是一份【同步讲义】（人教A版2019）高中数学选修第三册：拓展一：近八年统计案例高考真题分类汇编 讲义，文件包含同步讲义人教A版2019高中数学选修第三册拓展一近八年统计案例高考真题分类汇编原卷版docx、同步讲义人教A版2019高中数学选修第三册拓展一近八年统计案例高考真题分类汇编解析版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。

拓展一：近八年统计案例高考真题分类汇编

考点一 变量间的相关关系
考点二 相关系数
考点三 线性回归方程
考点四 独立性检验

考点一 变量间的相关关系
1．（2015•湖北）已知变量和满足关系，变量与正相关，下列结论中正确的是　　
A．与负相关，与负相关 B．与正相关，与正相关
C．与正相关，与负相关 D．与负相关，与正相关
【解析】因为变量和满足关系，一次项系数为，所以与负相关；
变量与正相关，设，，，所以，得到，一次项系数小于0，所以与负相关；
故选：．
2．（2015•北京）高三年级267位学生参加期末考试，某班37位学生的语文成绩，数学成绩与总成绩在全年级的排名情况如图所示，甲、乙、丙为该班三位学生．
从这次考试成绩看，
①在甲、乙两人中，其语文成绩名次比其总成绩名次靠前的学生是　　；
②在语文和数学两个科目中，丙同学的成绩名次更靠前的科目是　　．

【解析】①在甲、乙两人中，其语文成绩名次比其总成绩名次靠前的学生是乙；
②观察散点图，发现丙的总成绩在年级中的名次倒数第5，数学成绩的名次倒数第11，
语文成绩的名次倒数第4，丙同学的成绩名次更靠前的科目是数学．
故答案为：乙；数学．

考点二 相关系数
3．（2020•新课标Ⅱ）某沙漠地区经过治理，生态系统得到很大改善，野生动物数量有所增加．为调查该地区某种野生动物的数量，将其分成面积相近的200个地块，从这些地块中用简单随机抽样的方法抽取20个作为样区，调查得到样本数据，，2，，，其中和分别表示第个样区的植物覆盖面积（单位：公顷）和这种野生动物的数量，并计算得，，，，．
（1）求该地区这种野生动物数量的估计值（这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数）；
（2）求样本，，2，，的相关系数（精确到；
（3）根据现有统计资料，各地块间植物覆盖面积差异很大．为提高样本的代表性以获得该地区这种野生动物数量更准确地估计，请给出一种你认为更合理的抽样方法，并说明理由．
附：相关系数，．
【解析】（1）由已知，，
个样区野生动物数量的平均数为，
该地区这种野生动物数量的估计值为；
（2），，，
；
（3）更合理的抽样方法是分层抽样，根据植物覆盖面积的大小对地块分层，再对200个地块进行分层抽样．
理由如下：由（2）知各样区的这种野生动物数量与植物覆盖面积有很强的正相关．由于各地块间植物覆盖面积差异很大，从而各地块间这种野生动物数量差异也很大，采用分层抽样的方法较好地保持了样本结构与总体结构的一致性，提高了样本的代表性，从而可以获得该地区这种野生动物数量更准确地估计．
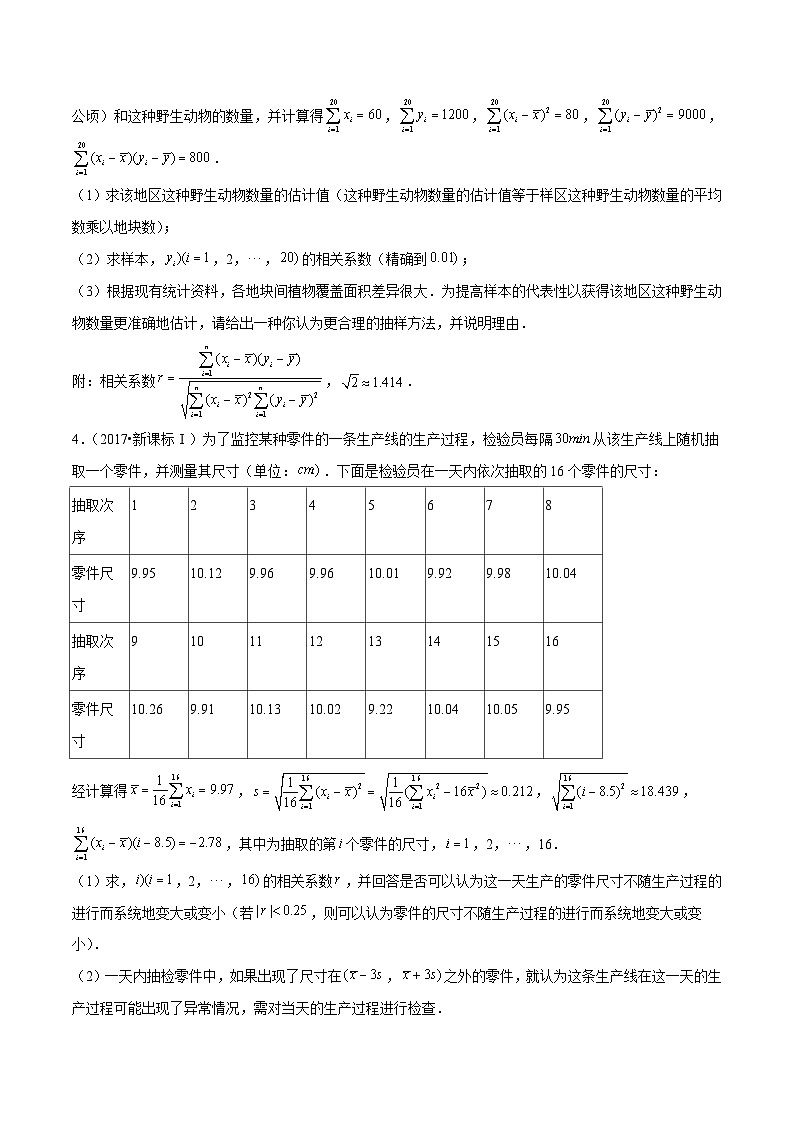
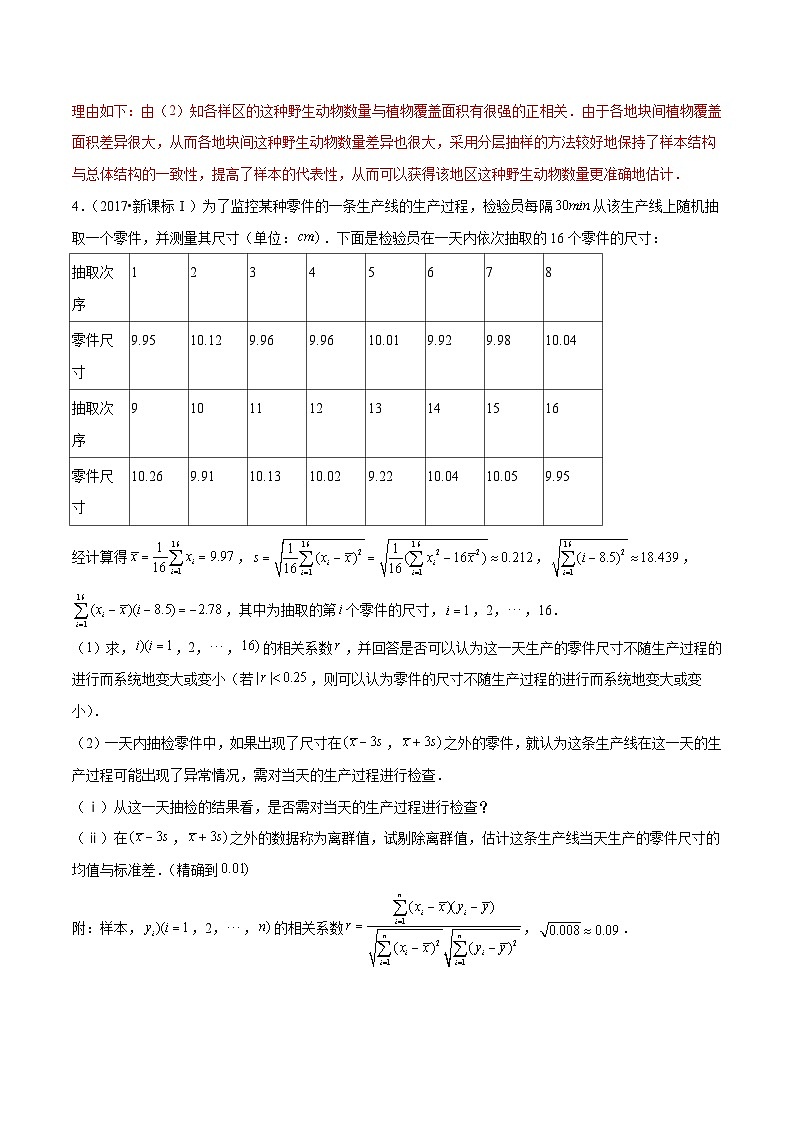
4．（2017•新课标Ⅰ）为了监控某种零件的一条生产线的生产过程，检验员每隔从该生产线上随机抽取一个零件，并测量其尺寸（单位：．下面是检验员在一天内依次抽取的16个零件的尺寸：
抽取次序
1
2
3
4
5
6
7
8
零件尺寸
9.95
10.12
9.96
9.96
10.01
9.92
9.98
10.04
抽取次序
9
10
11
12
13
14
15
16
零件尺寸
10.26
9.91
10.13
10.02
9.22
10.04
10.05
9.95
经计算得，，，，其中为抽取的第个零件的尺寸，，2，，16．
（1）求，，2，，的相关系数，并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小（若，则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小）．
（2）一天内抽检零件中，如果出现了尺寸在，之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．
（ⅰ）从这一天抽检的结果看，是否需对当天的生产过程进行检查？
（ⅱ）在，之外的数据称为离群值，试剔除离群值，估计这条生产线当天生产的零件尺寸的均值与标准差．（精确到
附：样本，，2，，的相关系数，．
【解析】（1）．
，可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小．
（2），，合格零件尺寸范围是，
显然第13号零件尺寸不在此范围之内，
需要对当天的生产过程进行检查．
剔除离群值后，剩下的数据平均值为，
，
剔除离群值后样本方差为，
剔除离群值后样本标准差为．

考点三 线性回归方程
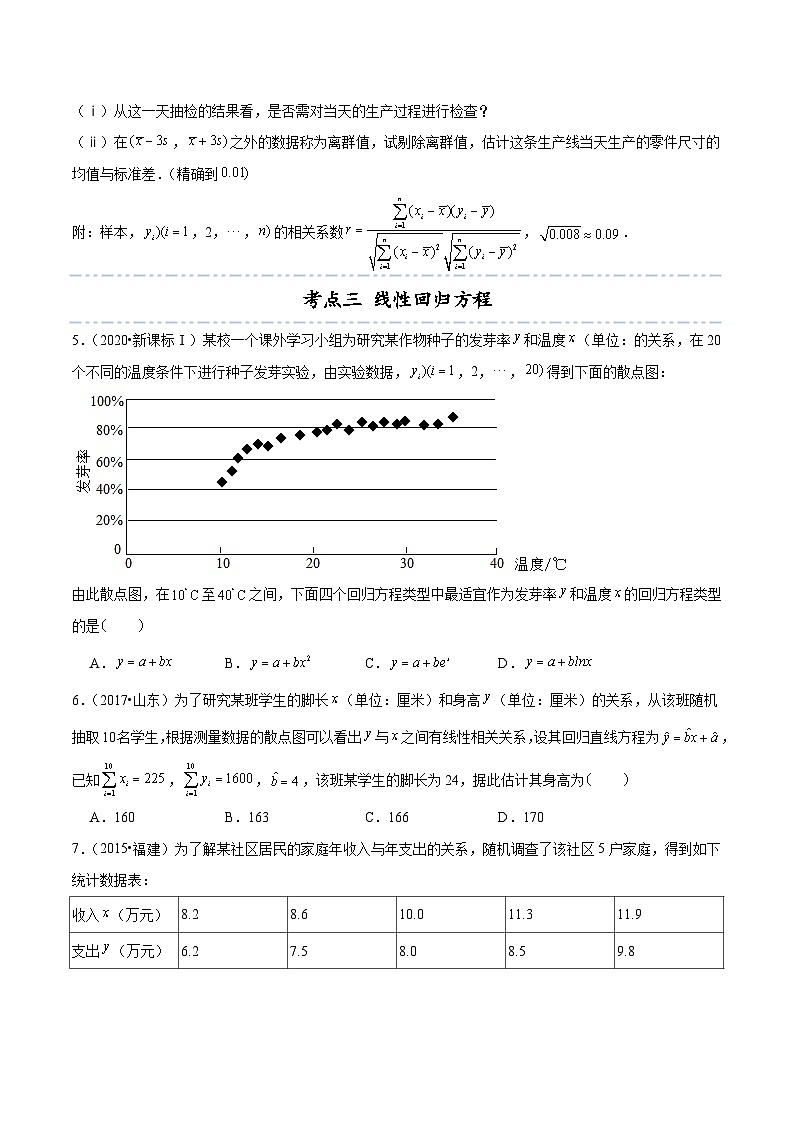
5．（2020•新课标Ⅰ）某校一个课外学习小组为研究某作物种子的发芽率和温度（单位：的关系，在20个不同的温度条件下进行种子发芽实验，由实验数据，，2，，得到下面的散点图：

由此散点图，在至之间，下面四个回归方程类型中最适宜作为发芽率和温度的回归方程类型的是　　
A． B． C． D．
【解析】由散点图可知，在至之间，发芽率和温度所对应的点在一段对数函数的曲线附近，
结合选项可知，可作为发芽率和温度的回归方程类型．
故选：．
6．（2017•山东）为了研究某班学生的脚长（单位：厘米）和身高（单位：厘米）的关系，从该班随机抽取10名学生，根据测量数据的散点图可以看出与之间有线性相关关系，设其回归直线方程为，已知，，，该班某学生的脚长为24，据此估计其身高为　　
A．160 B．163 C．166 D．170
【解析】由线性回归方程为，
则，，
则数据的样本中心点，
由回归直线方程样本中心点，则，
回归直线方程为，
当时，，
则估计其身高为166，
故选：．
7．（2015•福建）为了解某社区居民的家庭年收入与年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：
收入（万元）
8.2
8.6
10.0
11.3
11.9
支出（万元）
6.2
7.5
8.0
8.5
9.8
根据上表可得回归直线方程，其中，据此估计，该社区一户收入为15万元家庭年支出为　　
A．11.4万元 B．11.8万元 C．12.0万元 D．12.2万元
【解析】由题意可得，
，
代入回归方程可得，
回归方程为，
把代入方程可得，
故选：．
8．（2022•乙卷）某地经过多年的环境治理，已将荒山改造成了绿水青山．为估计一林区某种树木的总材积量，随机选取了10棵这种树木，测量每棵树的根部横截面积（单位：和材积量（单位：，得到如下数据：
样本号
1
2
3
4
5
6
7
8
9
10
总和
根部横截面积
0.04
0.06
0.04
0.08
0.08
0.05
0.05
0.07
0.07
0.06
0.6
材积量
0.25
0.40
0.22
0.54
0.51
0.34
0.36
0.46
0.42
0.40
3.9
并计算得，，．
（1）估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量；
（2）求该林区这种树木的根部横截面积与材积量的样本相关系数（精确到；
（3）现测量了该林区所有这种树木的根部横截面积，并得到所有这种树木的根部横截面积总和为．已知树木的材积量与其根部横截面积近似成正比．利用以上数据给出该林区这种树木的总材积量的估计值．
附：相关系数，．
【解析】（1）设这种树木平均一棵的根部横截面积为，平均一棵的材积量为，
则根据题中数据得：，；
（2）由题可知，；
（3）设总根部面积和，总材积量为，则，故．
9．（2018•新课标Ⅱ）如图是某地区2000年至2016年环境基础设施投资额（单位：亿元）的折线图．

为了预测该地区2018年的环境基础设施投资额，建立了与时间变量的两个线性回归模型．根据2000年至2016年的数据（时间变量的值依次为1，2，，建立模型①：；根据2010年至2016年的数据（时间变量的值依次为1，2，，建立模型②：．
（1）分别利用这两个模型，求该地区2018年的环境基础设施投资额的预测值；
（2）你认为用哪个模型得到的预测值更可靠？并说明理由．
【解析】（1）根据模型①：，
计算时，；
利用这个模型，求出该地区2018年的环境基础设施投资额的预测值是226.1亿元；
根据模型②：，
计算时，；
利用这个模型，求该地区2018年的环境基础设施投资额的预测值是256.5亿元；
（2）解法1：模型②得到的预测值更可靠，因为从总体数据看，该地区从2000年到2016年的环境基础设施投资额是逐年上升的，从2000年到2009年间递增的幅度较小些，从2010年到2016年间递增的幅度较大些，所以利用模型②的预测值更可靠些．
解法2，模型②对应的7个点分布宽度小于模型①对应的17个点的分布宽度，则，所以模型②较好；
解法3，选择与2018邻近的三个年份，2015，计算模型②对应的残差绝对值之和，模型①对应的残差绝对值之和；且，所以模型②较好；
所以利用模型②的预测值更可靠些．
10．（2016•新课标Ⅲ）如图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图．
注：年份代码分别对应年份．
（Ⅰ）由折线图看出，可用线性回归模型拟合与的关系，请用相关系数加以证明；
（Ⅱ）建立关于的回归方程（系数精确到，预测2016年我国生活垃圾无害化处理量．
附注：
参考数据：，，，．
参考公式：相关系数，
回归方程中斜率和截距的最小二乘估计公式分别为：
，．

【解析】（1）由折线图看出，与之间存在较强的正相关关系，理由如下：
，
，
故与之间存在较强的正相关关系；
（2），
，
关于的回归方程，
2016年对应的值为9，
故，
预测2016年我国生活垃圾无害化处理量为1.83亿吨．
11．（2015•重庆）随着我国经济的发展，居民的储蓄存款逐年增长．设某地区城乡居民人民币储蓄存款（年底余额）如下表：
年份
2010
2011
2012
2013
2014
时间代号
1
2
3
4
5
储蓄存款（千亿元）
5
6
7
8
10
（Ⅰ）求关于的回归方程．
（Ⅱ）用所求回归方程预测该地区2015年的人民币储蓄存款．
附：回归方程中
．
【解析】（Ⅰ）
由题意，，，
，，
，，
关于的回归方程．
（Ⅱ）时，（千亿元）．
12．（2015•新课标Ⅰ）某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费（单位：千元）对年销售量（单位：和年利润（单位：千元）的影响，对近8年的年宣传费和年销售量，2，，数据作了初步处理，得到下面的散点图及一些统计量的值．








46.6
563
6.8
289.8
1.6
1469
108.8
表中，
（Ⅰ）根据散点图判断，与哪一个适宜作为年销售量关于年宣传费的回归方程类型？（给出判断即可，不必说明理由）
（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立关于的回归方程；
（Ⅲ）已知这种产品的年利润与、的关系为．根据（Ⅱ）的结果回答下列问题：
年宣传费时，年销售量及年利润的预报值是多少？
年宣传费为何值时，年利润的预报值最大？
附：对于一组数据，，，，，，，其回归线的斜率和截距的最小二乘估计分别为：，．
【解析】（Ⅰ）由散点图可以判断，适宜作为年销售量关于年宣传费的回归方程类型；
（Ⅱ）令，先建立关于的线性回归方程，由于，
，
所以关于的线性回归方程为，
因此关于的回归方程为，
（Ⅲ）由（Ⅱ）知，当时，年销售量的预报值，
年利润的预报值，
根据（Ⅱ）的结果可知，年利润的预报值，
当时，即当时，年利润的预报值最大．
考点四 独立性检验
13．（2022•甲卷）甲、乙两城之间的长途客车均由和两家公司运营．为了解这两家公司长途客车的运行情况，随机调查了甲、乙两城之间的500个班次，得到下面列联表：

准点班次数
未准点班次数

240
20

210
30
（1）根据上表，分别估计这两家公司甲、乙两城之间的长途客车准点的概率；
（2）能否有的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关？
附：．

0.100
0.050
0.010

2.706
3.841
6.635
【解析】（1）公司一共调查了260辆车，其中有240辆准点，故公司准点的概率为；
公司一共调查了240辆车，其中有210辆准点，故公司准点的概率为；
（2）由题设数据可知，准点班次数共450辆，未准点班次数共50辆，公司共260辆，公司共240辆，
，
有的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关．
14．（2022•新高考Ⅰ）一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯（卫生习惯分为良好和不够良好两类）的关系，在已患该疾病的病例中随机调查了100例（称为病例组），同时在未患该疾病的人群中随机调查了100人（称为对照组），得到如下数据：

不够良好
良好
病例组
40
60
对照组
10
90
（1）能否有的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异？
（2）从该地的人群中任选一人，表示事件“选到的人卫生习惯不够良好”， 表示事件“选到的人患有该疾病”， 与的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标，记该指标为．
（ⅰ）证明：；
（ⅱ）利用该调查数据，给出，的估计值，并利用（ⅰ）的结果给出的估计值．
附：．

0.050
0.010
0.001

3.841
6.635
10.828
【解析】（1）补充列联表为：

不够良好
良好
合计
病例组
40
60
100
对照组
10
90
100
合计
50
150
200
计算，
所以有的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异．
（2）证明：；
（ⅱ）利用调查数据，，，，，
所以．
15．（2021•甲卷）甲、乙两台机床生产同种产品，产品按质量分为一级品和二级品，为了比较两台机床产品的质量，分别用两台机床各生产了200件产品，产品的质量情况统计如下表：

一级品
二级品
合计
甲机床
150
50
200
乙机床
120
80
200
合计
270
130
400
（1）甲机床、乙机床生产的产品中一级品的频率分别是多少？
（2）能否有的把握认为甲机床的产品质量与乙机床的产品质量有差异？
附：．

0.050
0.010
0.001

3.841
6.635
10.828
【解析】（1）由题意可得，甲机床、乙机床生产总数均为200件，
因为甲的一级品的频数为150，所以甲的一级品的频率为；
因为乙的一级品的频数为120，所以乙的一级品的频率为；
（2）根据列联表，可得
．
所以有的把握认为甲机床的产品质量与乙机床的产品质量有差异．
16．（2020•山东）为加强环境保护，治理空气污染，环境监测部门对某市空气质量进行调研，随机抽查了100天空气中的和浓度（单位：，得下表：

，
，
，
，
32
18
4
，
6
8
12
，
3
7
10
（1）估计事件“该市一天空气中浓度不超过75，且浓度不超过150”的概率；
（2）根据所给数据，完成下面的列联表：

，
，
，


，


（3）根据（2）中的列联表，判断是否有的把握认为该市一天空气中浓度与浓度有关？
附：

0.050
0.010
0.001

3.841
6.635
10.828


【解析】（1）用频率估计概率，从而得到“该市一天空气中浓度不超过75，且浓度不超过150”的概率；
（2）根据所给数据，可得下面的列联表：

（3）根据（2）中的列联表，
由，
；
故有的把握认为该市一天空气中浓度与浓度有关，
17．（2020•新课标Ⅲ）某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次，整理数据得到下表（单位：天）
锻炼人次
空气质量等级
，
，
，
1（优
2
16
25
2（良
5
10
12
3（轻度污染）
6
7
8
4（中度污染）
7
2
0
（1）分别估计该市一天的空气质量等级为1，2，3，4的概率；
（2）求一天中到该公园锻炼的平均人次的估计值（同一组中的数据用该组区间的中点值为代表）；
（3）若某天的空气质量等级为1或2，则称这天“空气质量好”；若某天的空气质量等级为3或4，则称这天“空气质量不好”．根据所给数据，完成下面的列联表，并根据列联表，判断是否有的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关？

人次
人次
空气质量好


空气质量不好


附：

0.050
0.010
0.001

3.841
6.635
10.828
【解析】（1）该市一天的空气质量等级为1的概率为：；
该市一天的空气质量等级为2的概率为：；
该市一天的空气质量等级为3的概率为：；
该市一天的空气质量等级为4的概率为：；
（2）由题意可得：一天中到该公园锻炼的平均人次的估计值为：
，
（3）根据所给数据，可得下面的列联表，

人次
人次
总计
空气质量好
33
37
70
空气质量不好
22
8
30
总计
55
45
100
由表中数据可得：，
所以有的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关．
18．（2019•新课标Ⅰ）某商场为提高服务质量，随机调查了50名男顾客和50名女顾客，每位顾客对该商场的服务给出满意或不满意的评价，得到下面列联表：

满意
不满意
男顾客
40
10
女顾客
30
20
（1）分别估计男、女顾客对该商场服务满意的概率；
（2）能否有的把握认为男、女顾客对该商场服务的评价有差异？
附：．

0.050
0.010
0.001

3.841
6.635
10.828
【解析】（1）由题中数据可知，男顾客对该商场服务满意的概率，
女顾客对该商场服务满意的概率；
（2）由题意可知，，
故有的把握认为男、女顾客对该商场服务的评价有差异．
19．（2018•新课标Ⅲ）某工厂为提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的生产方式．为比较两种生产方式的效率，选取40名工人，将他们随机分成两组，每组20人．第一组工人用第一种生产方式，第二组工人用第二种生产方式．根据工人完成生产任务的工作时间（单位：绘制了如下茎叶图：

（1）根据茎叶图判断哪种生产方式的效率更高？并说明理由；
（2）求40名工人完成生产任务所需时间的中位数，并将完成生产任务所需时间超过和不超过的工人数填入下面的列联表：

超过
不超过
第一种生产方式


第二种生产方式


（3）根据（2）中的列联表，能否有的把握认为两种生产方式的效率有差异？
附：，

0.050
0.010
0.001

3.841
6.635
10.828
【解析】（1）根据茎叶图中的数据知，
第一种生产方式的工作时间主要集中在之间，
第二种生产方式的工作时间主要集中在之间，
所以第二种生产方式的工作时间较少些，效率更高；
（2）这40名工人完成生产任务所需时间按从小到大的顺序排列后，
排在中间的两个数据是79和81，计算它们的中位数为；
由此填写列联表如下；

超过
不超过
总计
第一种生产方式
15
5
20
第二种生产方式
5
15
20
总计
20
20
40
（3）根据（2）中的列联表，计算
，
能有的把握认为两种生产方式的效率有差异．
20．（2017•新课标Ⅱ）海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：，其频率分布直方图如图：

（1）设两种养殖方法的箱产量相互独立，记表示事件“旧养殖法的箱产量低于，新养殖法的箱产量不低于”，估计的概率；
（2）填写下面列联表，并根据列联表判断是否有的把握认为箱产量与养殖方法有关：

箱产量
箱产量
旧养殖法


新养殖法


（3）根据箱产量的频率分布直方图，求新养殖法箱产量的中位数的估计值（精确到．
附：

0.050
0.010
0.001

3.841
6.635
10.828
．
【解析】（1）记表示事件“旧养殖法的箱产量低于”， 表示事件“新养殖法的箱产量不低于”，
由（A）（B）（C），
则旧养殖法的箱产量低于，
故（B）的估计值0.62，
新养殖法的箱产量不低于，
故（C）的估计值为，
则事件的概率估计值为（A）（B）（C）；
发生的概率为0.4092；
（2）列联表：

箱产量
箱产量
总计
旧养殖法
62
38
100
新养殖法
34
66
100
总计
96
104
200
则，
由，
有的把握认为箱产量与养殖方法有关；
（3）由新养殖法的箱产量频率分布直方图中，箱产量低于的直方图的面积：
，
箱产量低于的直方图面积为：
，
故新养殖法产量的中位数的估计值为：，
新养殖法箱产量的中位数的估计值．