2024版新教材高考数学全程一轮总复习课时作业四十二直线平面平行的判定与性质

这是一份2024版新教材高考数学全程一轮总复习课时作业四十二直线平面平行的判定与性质，共10页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

1．已知直线a、b和平面α，下面说法正确的是( )
A．若a∥b，b∥α，则a∥α
B．若a∥b，b⊂α，则a∥α
C．若a∥b，b⊂α，a⊄α，则a∥α
D．若a∥α，b∥α，则a∥b
2．[2023·湖北恩施期末]设a是直线，α是平面，则能推出a∥α的条件是( )
A．存在一条直线b，a∥b，b⊂α
B．存在一条直线b，a⊥b，b⊥α
C．存在一个平面β，a⊂β，α∥β
D．存在一个平面β，a⊥β，α⊥β
3．已知α，β是两个不重合的平面，在下列条件中，可确定α∥β的是( )
A．α，β都平行于直线l
B．l，m是两条异面直线，且l∥β，m∥β，l∥α，m∥α
C．α内有三个不共线的点到β的距离相等
D．l，m是α内两条直线，且l∥β，m∥β
4．如图，在四棱柱ABCD­A1B1C1D1中，平面ABB1A1∥平面CDD1C1，且AF∥EC1，则四边形AEC1F的形状是( )
A．平行四边形B．矩形
C．菱形D．正方形
5.
如图，已知P为四边形ABCD外一点，E，F分别为BD，PD上的点，若EF∥平面PBC，则( )
A．EF∥PAB．EF∥PB
C．EF∥PCD．以上均有可能
6．已知直线l∥平面α，点P∈平面α，那么过点P且平行于直线l的直线( )
A．有无数条，仅有一条在平面α内
B．只有一条，且不在平面α内
C．有无数条，均不在平面α内
D．只有一条，且在平面α内
7．(能力题)[2023·湖南湘潭模拟]已知直三棱柱ABC­A1B1C1的侧棱和底面边长均为1，M，N分别是棱BC，A1B1上的点，且CM＝2B1N＝λ，当MN∥平面AA1C1C时，λ的值为( )
A．eq \f(3,4) B．eq \f(2,3) C．eq \f(1,2) D．eq \f(1,3)
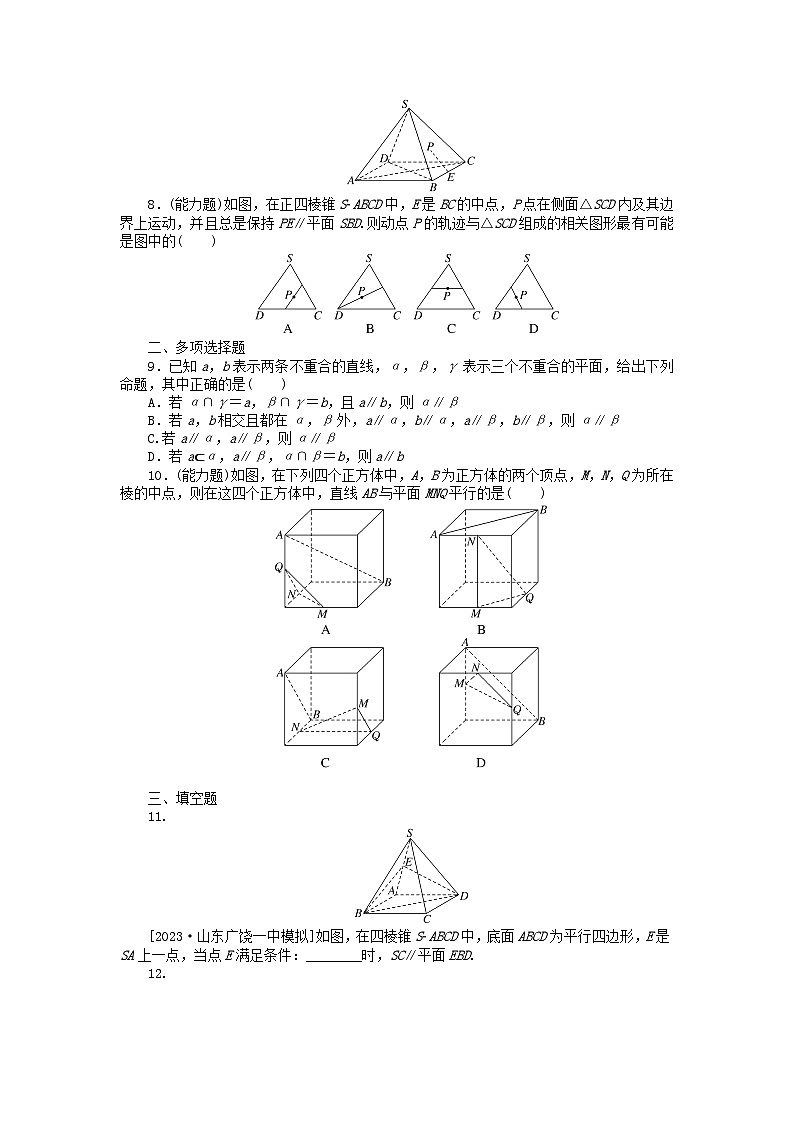
8．(能力题)如图，在正四棱锥S­ABCD中，E是BC的中点，P点在侧面△SCD内及其边界上运动，并且总是保持PE∥平面SBD.则动点P的轨迹与△SCD组成的相关图形最有可能是图中的( )
二、多项选择题
9．已知a，b表示两条不重合的直线，α，β，γ表示三个不重合的平面，给出下列命题，其中正确的是( )
A．若α∩γ＝a，β∩γ＝b，且a∥b，则α∥β
B．若a，b相交且都在α，β外，a∥α，b∥α，a∥β，b∥β，则α∥β
C.若a∥α，a∥β，则α∥β
D．若a⊂α，a∥β，α∩β＝b，则a∥b
10．(能力题)如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ平行的是( )
三、填空题
11.
[2023·山东广饶一中模拟]如图，在四棱锥S­ABCD中，底面ABCD为平行四边形，E是SA上一点，当点E满足条件：________时，SC∥平面EBD.
12.
(能力题)如图，在长方体ABCD­A1B1C1D1中，过BB1的中点E作一个与平面ACB1平行的平面交AB于点M，交BC于点N，则eq \f(MN,AC)＝________．
四、解答题
13．如图，在棱长为2的正方体ABCD­A1B1C1D1中，M为棱BB1的中点，P为棱A1D1的中点，平面DA1MN与平面CB1PQ将该正方体截成三个多面体，其中N，Q分别在棱BC，DD1上．
(1)求证：MN∥平面CB1PQ；
(2)求证：平面MNDA1∥平面CB1PQ.
14.
(能力题)如图所示的几何体中，底面ABCD是等腰梯形，AB∥CD，∠ABC＝60°，AA1⊥平面ABCD，CC1＝AA1，CC1∥AA1，且CD＝BC＝eq \f(1,2)AB＝eq \f(1,2)AA1，E，F分别为A1D，CC1的中点．证明：EF∥平面ABCD.
优生选做题
15.
[2023·安徽蚌埠模拟]如图，正方体ABCD­A1B1C1D1的一个截面经过顶点A，C及棱A1B1上一点K，截面将正方体分成体积比为2∶1的两部分，则eq \f(A1K,KB1)的值为( )
A．eq \f(2,3)B．eq \f(\r(5)＋1,2)
C．eq \f(\r(5)－1,2)D．eq \f(3－\r(5),2)
16.
如图，在四棱锥P­ABCD中，底面ABCD为平行四边形，E为棱PC的中点，平面ABE与棱PD交于点F．
(1)求证：PA∥平面BDE；
(2)求证：F为PD的中点；
(3)在棱AB上是否存在点N，使得FN∥平面BDE？若存在，求出eq \f(AN,NB)的值；若不存在，说明理由．
课时作业（四十二） 直线、平面平行的判定与性质
1．解析：对于A，若a∥b，b∥α，则a∥α或a⊂α，故A错误；
对于B，若a∥b，b⊂α，则a∥α或a⊂α，故B错误；
对于C，若a∥b，b⊂α，a⊄α，则a∥α，故C正确；
对于D，若a∥α，b∥α，则a∥b，a与b相交，或a与b异面，故D错误．
故选C.
答案：C
2．解析：对于A，若a⊂α，可满足a∥b，b⊂α，但无法得到a∥α，A错误；
对于B，若a⊂α，可满足a⊥b，b⊥α，但无法得到a∥α，B错误；
对于C，由面面平行的性质知：若α∥β，a⊂β，则a∥α，C正确；
对于D，若a⊂α，可满足a⊥β，α⊥β，但无法得到a∥α，D错误．
故选C.
答案：C
3．解析：
对于A，
平面ABCD与平面AA1B1B都平行于CD，但相交于AB，故A错误；
对于B，由于l，m是异面直线，所以l，m不平行，过m上的一点作l的平行线l′，
设m与l′共同确定的平面为γ，则由题意α∥γ，β∥γ，∴α∥β，
故B正确；
对于C，如图：
α∩β＝l，在β平面两侧α平面上分别存在A，B，C三个点到β的距离相等，
故C错误；
对于D，如果l∥m，则不能判定α∥β，故D错误．
故选B.
答案：B
4．解析：∵AF∥C1E，∴A，F，C1，E四点共面；
∵平面ABB1A1∥平面CDD1C1，平面ABB1A1∩平面AFC1E＝AE，平面CDD1C1∩平面AFC1E＝C1F，∴AE∥C1F，
∴四边形AEC1F为平行四边形．
故选A.
答案：A
5．解析：
因为EF∥平面PBC，且平面PBD∩平面PBC＝PB，EF⊂平面PBD，所以EF∥PB，故B正确．
若EF∥PA，则PA∥PB，这与PA∩PB＝P矛盾，∴EF与PA不平行，同理可得EF与PC不平行．
故选B.
答案：B
6．解析：过直线l与点P的平面有且只有一个，记该平面为β.
又因直线l∥平面α，点P∈平面α，
所以过点P且平行于直线l的直线只有一条，且这条线为平面α与平面β的相交线．
故选D.
答案：D
7．解析：
过N作NP∥B1C1交A1C1于P，连接CP，
因为MC∥B1C1，∴NP∥MC，故N，P，C，M共面，
因为MN∥平面AA1C1C，平面MNPC∩平面AA1C1C＝CP，MN⊂平面MNPC，
所以MN∥CP，又NP∥MC，
∴四边形MNPC为平行四边形，
又CM＝2B1N＝λ，
∴NP＝1－eq \f(λ,2)＝λ＝CM，
所以λ＝eq \f(2,3).
故选B.
答案：B
8．解析：
分别取CD、SC的中点M、N，连接MN，ME，NE，
又∵E是BC的中点，∴EM∥BD，EN∥SB，
又∵EM，EN⊄平面SBD，BD，SB⊂平面SBD，∴EM∥平面SBD，EN∥平面SBD，
又∵EM∩EN＝E，EM，EN⊂平面EMN，∴平面EMN∥平面SBD，
∴当P在MN上移动时，PE⊂平面EMN，此时能够保持PE∥平面SBD，
则动点P的轨迹与△SCD组成的相关图形是选项A.
故选A.
答案：A
9．解析：对于A，当α∩γ＝a，β∩γ＝b，且a∥b时，α与β有可能平行，也可能相交，所以A错误，
对于B，设a，b确定的平面为γ，因为a∥α，b∥α，a∥β，b∥β，a，b是相交直线，所以γ∥α，γ∥β，故α∥β，所以B正确，
对于C，当a∥α，a∥β时，α与β可能平行，也可能相交，所以C错误，
对于D，当a⊂α，a∥β，α∩β＝b时，由线面平行的性质定理可知a∥b，所以D正确．
故选BD.
答案：BD
10．解析：
对A，如图，易得平面MNQ∥平面ACD，但平面ACD与AB相交，故直线AB与平面MNQ不平行；
对B，如图，C为所在棱的中点，根据中位线的性质有NC∥AB，且MN∥CQ，MN＝CQ，故四边形MNCQ是平行四边形，故NC∥MQ，故AB∥MQ，故直线AB与平面MNQ平行；
对C，根据中位线与平行四边形的性质，同理可得AB∥MQ，直线AB与平面MNQ平行；
对D，根据中位线与平行四边形的性质，同理可得AB∥NQ，直线AB与平面MNQ平行．
故选BCD.
答案：BCD
11．解析：
连接AC交BD于O，连接OE，
∵SC∥平面EBD，SC⊂平面SAC，平面SAC∩平面EBD＝OE，
∴SC∥OE.
又∵底面ABCD为平行四边形，O为对角线AC与BD的交点，
故O为AC的中点，∴E为SA的中点，
故当E满足条件：SE＝AE时，SC∥平面EBD.
答案：SE＝AE（答案表述不唯一）
12．解析：∵平面MNE∥平面ACB1，平面MNE∩平面ABB1A1＝EM，平面ACB1∩平面ABB1A1＝B1A，平面MNE∩平面CBB1C1＝EN，平面ACB1∩平面CBB1C1＝B1C，
∴由两个平面平行的性质定理可得EN∥B1C，EM∥B1A.
∴eq \f(BE,EB1)＝eq \f(BM,AM)，eq \f(BE,EB1)＝eq \f(BN,NC)，
又∵E为BB1的中点，
∴M，N分别为BA，BC的中点，
∴MN＝eq \f(1,2)AC，即eq \f(MN,AC)＝eq \f(1,2).
答案：eq \f(1,2)
13．证明：（1）由题意得平面BCC1B1∥平面ADD1A1，
又∵平面MNDA1∩平面BCC1B1＝MN，
平面MNDA1∩平面ADD1A1＝A1D，∴A1D∥MN，
同理PQ∥B1C，又∵A1B1∥AB且A1B1＝AB，AB∥CD且AB＝CD，
∴A1B1∥CD且A1B1＝CD，∴四边形A1B1CD为平行四边形，∴A1D∥B1C，∴MN∥PQ，又∵MN⊄平面CB1PQ，PQ⊂平面CB1PQ，
∴MN∥平面CB1PQ.
（2）由（1）MN∥B1C，∵M为BB1中点，∴N为BC中点，
同理Q为DD1中点，
连接B1Q，MD，∵BB1∥DD1，B1M＝eq \f(1,2)B1B＝eq \f(1,2)DD1＝QD，
∴四边形B1QDM为平行四边形，∴B1Q∥MD，又∵B1Q⊂平面CB1PQ，
且DM⊄平面CB1PQ，∴DM∥平面CB1PQ，又∵MN∥平面CB1PQ.
且DM∩MN＝M，DM，MN⊂平面MNDA1，
∴平面MNDA1∥平面CB1PQ.
14．证明：
取AA1的中点G，连接EG，FG，AC，
因为EG∥AD，EG⊄平面ABCD，AD⊂平面ABCD，
所以EG∥平面ABCD.
因为AG∥CF，AG＝CF，所以四边形AGFC是平行四边形，
FG∥AC，又FG⊄平面ABCD，AC⊂平面ABCD，
所以FG∥平面ABCD.
因为FG∩EG＝G，FG，EG⊂平面EFG，
所以平面EFG∥平面ABCD.
因为EF⊂平面ABCD，所以EF∥平面ABCD.
15．解析：
设正方体棱长为1，KB1＝x，
如图所示，该截面把正方体分为几何体ABC­KB1M和另一几何体，
由面面平行的性质可知：KM∥AC，
延长AK，CM，相交于点O，则O∈平面ABB1A1，且O∈平面BCC1B1，
又平面ABB1A1∩平面BCC1B1＝BB1，
所以O在直线BB1上，即AK，CM，BB1三线共点，
所以几何体ABC­KB1M为三棱台，
其中三棱台ABC­KB1M上底面积是eq \f(1,2)x2，下底面积为eq \f(1,2)，高等于1，
所以V＝eq \f(1,3)（eq \f(1,2)＋eq \f(1,2)x2＋eq \r(\f(1,2)×\f(1,2)x2)）×1＝eq \f(1,3)，解得：x＝eq \f(\r(5)－1,2)，
所以A1K＝1－eq \f(\r(5)－1,2)＝eq \f(3－\r(5),2)，eq \f(A1K,KB1)＝eq \f(3－\r(5),2)×eq \f(2,\r(5)－1)＝eq \f(\r(5)－1,2).
故选C.
答案：C
16．证明：
（1）连接AC、BD交于G，连接GE，如图：
由ABCD为平行四边形，则G为AC中点，又E为棱PC的中点，
所以GE为中位线，则GE∥PA，
又GE⊂平面BDE，PA⊄平面BDE，故PA∥平面BDE.
（2）由题设知：CD∥AB，AB⊂平面ABEF，CD⊄平面ABEF，
所以CD∥平面ABEF，又CD⊂平面PDC，平面PDC∩平面ABEF＝EF，
所以CD∥EF，又E为棱PC的中点，即EF是△PDC的中位线，
故F为PD的中点．
（3）存在N使得FN∥平面BDE且eq \f(AN,NB)＝1，理由如下：
H为AB中点，连接FH，
由题设BH＝eq \f(1,2)AB＝eq \f(1,2)CD且BH∥CD，由（2）知CD∥EF且EF＝eq \f(1,2)CD，
所以BH∥EF且BH＝EF，即BHFE为平行四边形，
所以FH∥BE，而BE⊂平面BDE，FH⊄平面BDE，
所以FH∥平面BDE，故所求N点即为H点，
则AB上存在点N使得FN∥平面BDE，且eq \f(AN,NB)＝1.