(新高考)高考数学一轮复习课时练习8.3《直线、平面平行的判定与性质》(含解析)

这是一份(新高考)高考数学一轮复习课时练习8.3《直线、平面平行的判定与性质》(含解析)，共22页。试卷主要包含了平行关系中的三个重要结论等内容，欢迎下载使用。
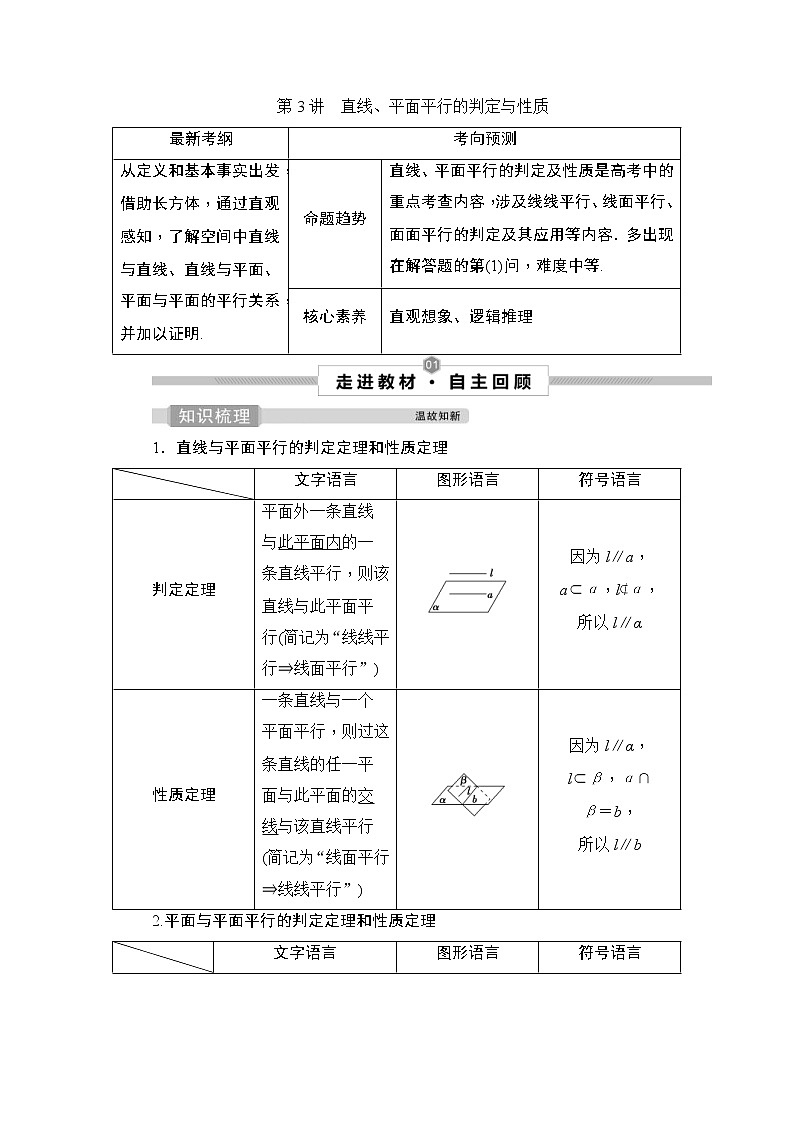
第3讲　直线、平面平行的判定与性质
最新考纲
考向预测
从定义和基本事实出发，借助长方体，通过直观感知，了解空间中直线与直线、直线与平面、平面与平面的平行关系，并加以证明.
命题趋势
直线、平面平行的判定及性质是高考中的重点考查内容，涉及线线平行、线面平行、面面平行的判定及其应用等内容．多出现在解答题的第(1)问，难度中等.
核心素养
直观想象、逻辑推理


1．直线与平面平行的判定定理和性质定理

文字语言
图形语言
符号语言
判定定理
平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行(简记为“线线平行⇒线面平行”)

因为l∥a，
a⊂α，l⊄α，
所以l∥α
性质定理
一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行⇒线线平行”)

因为l∥α，
l⊂β，α∩
β＝b，
所以l∥b
2.平面与平面平行的判定定理和性质定理

文字语言
图形语言
符号语言
判定定理
一个平面内的两条相交直线与另一个平面平行，则这两个平面平行(简记为“线面平行⇒面面平行”)

因为a∥β，
b∥β，a∩
b＝P，
a⊂α，b⊂α，
所以α∥β
性质定理
如果两个平行平面同时和第三个平面相交，那么它们的交线平行

因为α∥β，
α∩γ＝a，
β∩γ＝b，
所以a∥b
常用结论
1．三种平行关系的转化：
线线平行线面平行面面性质定理平行
线线平行、线面平行、面面平行的相互转化是解决与平行有关的证明题的指导思想．
2．平行关系中的三个重要结论
(1)垂直于同一条直线的两个平面平行，即若a⊥α，a⊥β，则α∥β.
(2)垂直于同一个平面的两条直线平行，即若a⊥α，b⊥α，则a∥b.
(3)平行于同一个平面的两个平面平行，即若α∥β，β∥γ，则α∥γ.
常见误区
1．在推证线面平行时，一定要强调直线不在平面内，否则会出现错误．
2．解题中注意符号语言的规范应用．

1．判断正误(正确的打“√”，错误的打“×”)
(1)直线l平行于平面α内的无数条直线，则l∥α.(　　)
(2)若直线l在平面α外，则l∥α.(　　)
(3)若直线l∥b，直线b⊂α，则l∥α.(　　)
(4)若直线l∥b，直线b⊂α，那么直线l就平行于平面α内的无数条直线．(　　)
答案：(1)×　(2)×　(3)×　(4)√
2．(易错题)平面α∥平面β的一个充分条件是(　　)
A．存在一条直线a，a∥α，a∥β
B．存在一条直线a，a⊂α，a∥β
C．存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥α
D．存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α
解析：选D.若α∩β＝l，a∥l，a⊄α，a⊄β，a∥α，a∥β，故排除A.若α∩β＝l，a⊂α，a∥l，则a∥β，故排除B.若α∩β＝l，a⊂α，a∥l，b⊂β，b∥l，则a∥β，b∥α，故排除C.
3．如图，长方体ABCD­A1B1C1D1中，E为DD1的中点，则BD1与平面AEC的位置关系为________．

解析：连接BD，设BD∩AC＝O，连接EO，

在△BDD1中，E为DD1的中点，O为BD的中点，
所以EO为△BDD1的中位线，则BD1∥EO，
而BD1⊄平面ACE，EO⊂平面ACE，
所以BD1∥平面ACE.
答案：平行
4．如图是长方体被一平面所截得的几何体，四边形EFGH为截面，则四边形EFGH的形状为________．
解析：因为平面ABFE∥平面DCGH，又平面EFGH∩平面ABFE＝EF，平面EFGH∩平面DCGH＝HG，所以EF∥HG.同理EH∥FG，所以四边形EFGH是平行四边形．
答案：平行四边形


与线、面平行相关命题的判定
[题组练透]
1．已知a，b表示直线，α，β，γ表示平面，则下列推理正确的是(　　)
A．α∩β＝a，b⊂α⇒a∥b
B．α∩β＝a，a∥b⇒b∥α且b∥β
C．a∥β，b∥β，a⊂α，b⊂α⇒α∥β
D．α∥β，α∩γ＝a，β∩γ＝b⇒a∥b
解析：选D.选项A中，α∩β＝a，b⊂α，则a，b可能平行也可能相交，故A不正确；
选项B中，α∩β＝a，a∥b，则可能b∥α且b∥β，也可能b在平面α或平面β内，故B不正确；
选项C中，a∥β，b∥β，a⊂α，b⊂α，根据面面平行的判定定理，再加上条件直线a与直线b相交，才能得出α∥β，故C不正确；选项D为面面平行性质定理的符号语言．
2．(多选)已知m，n为两条不重合的直线，α，β为两个不重合的平面，则下列说法正确的是(　　)
A．若m∥α，n∥β且α∥β，则m∥n
B．若m∥n，m⊥α，n⊥β，则α∥β
C．若m∥n，n⊂α，α∥β，m⊄β，则m∥β
D．若m∥n，n⊥α，α⊥β，则m∥β
解析：选BC.若m∥α，n∥β且α∥β，则m，n也可能异面或相交，故A错误；若m∥n，m⊥α，则n⊥α，又n⊥β，故α∥β，B正确；若m∥n，n⊂α，则m∥α或m⊂α，又α∥β，m⊄β，故m∥β，C正确；若m∥n，n⊥α，则m⊥α，又α⊥β，则m∥β或m⊂β，D错误．故选BC.
3．(多选)如图，若Ω是长方体ABCD­A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体，其中E为线段A1B1上异于B1的点，F为线段BB1上异于B1的点，且EH∥A1D1，则下列结论正确的是(　　)

A．EH∥FG
B．四边形EFGH是矩形
C．Ω是棱柱
D．四边形EFGH可能为梯形
解析：选ABC.因为EH∥A1D1，A1D1∥B1C1，所以EH∥B1C1，由EH⊄平面BCC1B1，B1C1⊂平面BCC1B1，所以EH∥平面BCC1B1，又EH⊂平面EFGH，平面EFGH∩平面BCC1B1＝FG，所以EH∥FG，所以A正确．由EH⊥平面A1ABB1，得EH⊥EF.由A项知FG∥EH，则FG⊥EF，同理，EH⊥HG，FG⊥HG，所以四边形EFGH为矩形，所以B正确，D错误．Ω是一个五棱柱，C正确．故选ABC.

直线、平面平行的判定方法
(1)关注是否符合判定定理与性质定理，并注意定理中易忽视的条件．
(2)结合题意构造或绘制图形，结合图形作出判断．
(3)利用实物进行空间想象，比较判断．

线面平行的判定与性质
角度一　线面平行的证明
如图，四边形ABCD为矩形，ED⊥平面ABCD，AF∥ED.求证：BF∥平面CDE.

【证明】　方法一：如图，在ED上取点N，使DN＝AF，连接NC，NF，
因为AF∥DN且AF＝DN，
所以四边形ADNF为平行四边形，
所以AD∥FN且AD＝FN，
又四边形ABCD为矩形，AD∥BC
且AD＝BC，所以FN∥BC且FN＝BC，
所以四边形BCNF为平行四边形，所以BF∥NC，
因为BF⊄平面CDE，NC⊂平面CDE，所以BF∥平面CDE.
方法二：因为四边形ABCD为矩形，所以AB∥CD，
因为AB⊄平面CDE，CD⊂平面CDE，
所以AB∥平面CDE；
又AF∥ED，因为AF⊄平面CDE，ED⊂平面CDE，
所以AF∥平面CDE；
因为AF∩AB＝A，AB⊂平面ABF，AF⊂平面ABF，
所以平面ABF∥平面CDE，
又BF⊂平面ABF，
所以BF∥平面CDE.

证明直线与平面平行的常用方法
(1)利用线面平行的定义．
(2)利用线面平行的判定定理：关键是找到平面内与已知直线平行的直线，可先直观判断题中是否存在这样的直线，若不存在，则需作出直线，常考虑利用三角形的中位线、平行四边形的对边平行或过已知直线作一平面，找其交线进行证明．　
角度二　线面平行性质的应用
如图，在五面体ABCDFE中，底面ABCD为矩形，EF∥AB，过BC的平面交棱FD于点P，交棱FA于点Q.
证明：PQ∥平面ABCD.

【证明】　因为底面ABCD为矩形，所以AD∥BC.
因为AD∥BC，AD⊂平面ADF，BC⊄平面ADF，所以BC∥平面ADF.
因为BC∥平面ADF，BC⊂平面BCPQ，平面BCPQ∩平面ADF＝PQ，所以BC∥PQ.因为PQ∥BC，PQ⊄平面ABCD，BC⊂平面ABCD，所以PQ∥平面ABCD.

应用线面平行的性质定理的关键是确定交线的位置，有时需要经过已知直线作辅助平面来确定交线．该定理的作用是由线面平行转化为线线平行．　

1．如图，在正方体ABCD­A1B1C1D1中，AB＝2，点E为AD的中点，点F在CD上．若EF∥平面AB1C，则线段EF的长度为________．

解析：在正方体ABCD­A1B1C1D1中，AB＝2，所以AC＝2.又E为AD中点，EF∥平面AB1C，EF⊂平面ABCD，平面ABCD∩平面AB1C＝AC，所以EF∥AC，所以F为DC的中点．
故EF＝AC＝.
答案：
2．如图所示，已知四边形ABCD是正方形，四边形ACEF是矩形，AB＝2，AF＝1，M是线段EF的中点．

(1)求证：AM∥平面BDE；
(2)若平面ADM∩平面BDE＝l，平面ABM∩平面BDE＝m，试分析l与m的位置关系，并证明你的结论．
解：(1)证明：如图，记AC与BD的交点为O，连接OE.
因为O，M分别是AC，EF的中点，四边形ACEF是矩形，
所以四边形AOEM是平行四边形，所以AM∥OE.
又因为OE⊂平面BDE，AM⊄平面BDE，
所以AM∥平面BDE.
(2)l∥m，证明如下：由(1)知AM∥平面BDE，
又AM⊂平面ADM，平面ADM∩平面BDE＝l，
所以l∥AM，同理，AM∥平面BDE，
又AM⊂平面ABM，平面ABM∩平面BDE＝m，
所以m∥AM，所以l∥m.

面面平行的判定与性质
如图所示，在三棱柱ABC­A1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证：

(1)B，C，H，G四点共面；
(2)平面EFA1∥平面BCHG.
【证明】　(1)因为G，H分别是
A1B1，A1C1的中点，
所以GH∥B1C1，又B1C1∥BC，
所以GH∥BC，所以B，C，H，G四点共面．
(2)在△ABC中，E，F分别为AB，AC的中点，
所以EF∥BC，因为EF⊄平面BCHG，BC⊂平面BCHG，所以EF∥平面BCHG.
又因为G，E分别为A1B1，AB的中点，
所以A1G綊EB，所以四边形A1EBG是平行四边形，
所以A1E∥GB.
因为A1E⊄平面BCHG，GB⊂平面BCHG，
所以A1E∥平面BCHG.
又因为A1E∩EF＝E，所以平面EFA1∥平面BCHG.
【引申探究】
1．(变条件、变问法)在本例条件下，若D为BC1的中点，求证：HD∥平面A1B1BA.
证明：如图所示，连接HD，A1B，

因为D为BC1的中点，
H为A1C1的中点，所以HD∥A1B，
又HD⊄平面A1B1BA，
A1B⊂平面A1B1BA，
所以HD∥平面A1B1BA.
2．(变条件、变问法)在本例条件下，若D1，D分别为B1C1，BC的中点，求证：平面A1BD1∥平面AC1D.
证明：如图所示，连接A1C交AC1于点M，
因为四边形A1ACC1是平行四边形，
所以M是A1C的中点，连接MD，
因为D为BC的中点，
所以A1B∥DM.
因为A1B⊂平面A1BD1，DM⊄平面A1BD1，
所以DM∥平面A1BD1.
又由三棱柱的性质知，D1C1綊BD，
所以四边形BDC1D1为平行四边形，
所以DC1∥BD1.
又DC1⊄平面A1BD1，BD1⊂平面A1BD1，
所以DC1∥平面A1BD1，
又因为DC1∩DM＝D，DC1，DM⊂平面AC1D，
所以平面A1BD1∥平面AC1D.

　

1．如图，AB∥平面α∥平面β，过点A，B的直线m，n分别交α，β于点C，E和点D，F，若AC＝2，CE＝3，BF＝4，则BD的长为(　　)

A.　　　　　　　　 B.
C. D.
解析：选C.由AB∥α∥β，易证 ＝.
即＝，所以BD＝＝＝.
2．如图，四边形ABCD为矩形，A，E，B，F四点共面，且△ABE和△ABF均为等腰直角三角形，∠BAE＝∠AFB＝90°.求证：平面BCE∥平面ADF.

证明：因为四边形ABCD为矩形，
所以BC∥AD，
又BC⊄平面ADF，AD⊂平面ADF，
所以BC∥平面ADF.
因为△ABE和△ABF均为等腰直角三角形，且∠BAE＝∠AFB＝90°，
所以∠BAF＝∠ABE＝45°，所以AF∥BE，
又BE⊄平面ADF，AF⊂平面ADF，
所以BE∥平面ADF，
因为BC∥平面ADF，BE∥平面ADF，
BC∩BE＝B，BC，BE⊂平面BCE，所以平面BCE∥平面ADF.

思想方法系列13　函数与方程思想在立体几何中的应用
如图所示，在四面体ABCD中，截面EFGH平行于对棱AB和CD，试问截面在什么位置时， 其截面面积最大？
【解】　因为AB∥平面EFGH，
平面EFGH与平面ABC和平面ABD分别交于FG，EH.所以AB∥FG，AB∥EH，
所以FG∥EH，同理可证EF∥GH，
所以截面EFGH是平行四边形．
设AB＝a，CD＝b，∠FGH＝α(α即为异面直线AB和CD所成的角或其补角)．
又设FG＝x，GH＝y，则由平面几何知识可得＝，＝，两式相加得＋＝1，即y＝(a－x)，所以S▱EFGH＝FG·GH·sin α＝x··(a－x)·sin α＝x(a－x)．
因为x>0，a－x>0且x＋(a－x)＝a为定值，
所以当且仅当x＝a－x时，x(a－x)＝，
此时x＝，y＝.
即当截面EFGH的顶点E，F，G，H为棱AD，AC，BC，BD的中点时截面面积最大．

(1)立体几何中的最值或范围问题，常用函数思想来解决．
(2)常见问题是求几何体截面面积或周长的最值或范围，动点的轨迹等，解题关键是通过对几何体中条件的分析和转化，设出未知量，建立函数关系式或轨迹方程．　
如图所示，侧棱与底面垂直，且底面为正方形的四棱柱ABCD­A1B1C1D1中，AA1＝2，AB＝1，M，N
分别在AD1，BC上移动，始终保持MN∥平面DCC1D1，设BN＝x，MN＝y，则函数y＝f(x)的图象大致是(　　)


解析：选C.过M作MQ∥DD1交AD于点Q，连接QN.
因为MQ⊄平面DCC1D1，DD1⊂平面DCC1D1，
所以MQ∥平面DCC1D1.
因为MN∥平面DCC1D1，
MN∩MQ＝M，所以平面MNQ∥平面DCC1D1.
又平面ABCD与平面MNQ和平面DCC1D1分别交于QN和DC，
所以NQ∥DC，可得QN＝CD＝AB＝1，AQ＝BN＝x，
因为＝＝2，所以MQ＝2x.
在Rt△MQN中，MN2＝MQ2＋QN2，即y2＝4x2＋1，
所以y2－4x2＝1(x≥0，y≥1)，
所以函数y＝f(x)的图象为焦点在y轴上的双曲线上支的一部分．

[A级　基础练]
1．(2020·宁波市北仑中学高三二模)下列命题中正确的是(　　)
A．若a，b是两条直线，且a∥b，那么a平行于经过b的任何平面
B．若直线a和平面α满足a∥α，那么a与α内的任何直线平行
C．平行于同一条直线的两个平面平行
D．若直线a，b和平面α满足a∥b，a∥α，b⊄α，则b∥α
解析：选D.A中，a可以在过b的平面内；B中，a与α内的直线也可能异面；C中，两平面可能相交；D中，由直线与平面平行的判定定理知b∥α，正确．
2．如图所示，在空间四边形ABCD中，E，F分别为边AB，AD上的点，且AE∶EB＝AF∶FD＝1∶4，又H，G分别为BC，CD的中点，则(　　)

A．BD∥平面EFGH，且四边形EFGH是矩形
B．EF∥平面BCD，且四边形EFGH是梯形
C．HG∥平面ABD，且四边形EFGH是菱形
D．EH∥平面ADC，且四边形EFGH是平行四边形
解析：选B.由AE∶EB＝AF∶FD＝1∶4知EF綊BD，又EF⊄平面BCD，BD⊂平面BCD，所以EF∥平面BCD.又H，G分别为BC，CD的中点，所以HG綊BD，所以EF∥HG且EF≠HG.所以四边形EFGH是梯形．
3．在四棱锥P­ABCD中，底面ABCD是平行四边形，E∈PC，F∈PB，＝3，＝λ，如图．若AF∥平面BDE，则λ的值为(　　)

A．1　　　　　　　　　　 B．3
C．2 D．4
解析：选C.连接AC，交BD于点O，连接OE.因为AF∥平面 BDE，所以过点A作AH∥平面BDE，交PC于点H，连接FH，则得到平面AFH∥平面BDE，所以FH∥BE.因为四边形ABCD为平行四边形，所以在△ACH与△OCE中，＝＝1，

即EC＝EH.又因为＝3，所以PH＝2HE.因为＝＝2，所以λ＝2.故选C.
4(多选)已知m，n为两条不同的直线，α，β为两个不同的平面，则下列说法错误的是(　　)
A．若m⊥α，m⊥n，则n∥α
B．若m⊥α，n∥β且α∥β，则m⊥n
C．若m⊂α，n⊂α且m∥β，n∥β，则α∥β
D．若直线m，n与平面α所成的角相等，则m∥n
解析：选ACD.对于A，满足m⊥α，m⊥n的n，α的位置关系可能是n∥α或n⊂α，故A错误；对于B，由m⊥α，α∥β，得m⊥β，结合n∥β，知m⊥n，故B正确；对于C，根据面面平行的判定定理知需当m，n为相交直线时，才有α∥β，故C错误；对于D，若m，n为圆锥的两条母线，平面α为圆锥的底面所在平面，此时直线m，n与平面α所成的角相等，但此时m，n为相交直线，故D错误．
5．(多选)在正方体ABCD­A1B1C1D1中，E，F，G分别是A1B1，B1C1，BB1的中点，下列四个推断中正确的是(　　)

A．FG∥平面AA1D1D
B．EF∥平面BC1D1
C．FG∥平面BC1D1
D．平面EFG∥平面BC1D1
解析：选AC.因为在正方体ABCD­A1B1C1D1中，F，G分别是B1C1，BB1的中点，
所以FG∥BC1，因为BC1∥AD1，
所以FG∥AD1，
因为FG⊄平面AA1D1D，AD1⊂平面AA1D1D，
所以FG∥平面AA1D1D，故A正确；
因为EF∥A1C1，A1C1与平面BC1D1相交，
所以EF与平面BC1D1相交，故B错误；
因为F，G分别是B1C1，BB1的中点，
所以FG∥BC1，因为FG⊄平面BC1D1，BC1⊂平面BC1D1，
所以FG∥平面BC1D1，故C正确；
因为EF与平面BC1D1相交，
所以平面EFG与平面BC1D1相交，故D错误．
故选AC.
6．在下面给出的条件中，若条件足够推出a∥α，则在横线上填“OK”；若条件不能保证推出a∥α，则请在横线上补足条件：
(1)条件：a∥b，b∥c，c⊂α，______，结论：a∥α；
(2)条件：α∩β＝b，a∥b，a⊂β，______，结论：a∥α.
解析：因为a∥b，b∥c，c⊂α，所以由直线与平面平行的判定定理得，当a⊄α时，a∥α.因为α∩β＝b，a∥b，a⊂β，则由直线与平面平行的判定定理得a∥α.
答案：(1)a⊄α　(2)OK
7．在四面体A­BCD中，M，N分别是△ACD，△BCD的重心，则四面体的四个面中与MN平行的是________．
解析：如图，取CD的中点E，连接AE，BE，
则EM∶MA＝1∶2，
EN∶BN＝1∶2，
所以MN∥AB.
因为AB⊂平面ABD，MN⊄平面ABD，AB⊂平面ABC，MN⊄平面ABC，
所以MN∥平面ABD，MN∥平面ABC.
答案：平面ABD与平面ABC
8．在三棱锥P­ABC中，D，E分别是PB，BC的中点，若F在线段AC上，且满足AD∥平面PEF，则的值为________．
解析：连接DC，交PE于点G，连接FG，DE，因为AD∥平面PEF，AD⊂平面ADC，平面ADC∩平面PEF＝FG，所以AD∥FG.因为D，E分别是PB，BC的中点，所以DE为△BPC的中位线，所以△DEG∽△CPG，可得＝＝，所以＝＝.

答案：
9．在如图所示的一块木料中，棱BC平行于平面A′B′C′D′.

(1)要经过平面A′B′C′D′内的一点P和棱BC将木料锯开，应怎样画线？
(2)所画的线与平面ABCD是什么位置关系？并证明你的结论．
解：(1)过点P作B′C′的平行线，
交A′B′，C′D′于点E，F，
连接BE，CF.
作图如右．
(2)EF∥平面ABCD.理由如下：
因为BC∥平面A′B′C′D′，
又因为平面B′C′CB∩平面A′B′C′D′＝B′C′，
所以BC∥B′C′，因为EF∥B′C′，所以EF∥BC，
又因为EF⊄平面ABCD，BC⊂平面ABCD，
所以EF∥平面ABCD.
10．如图，四边形ABCD与ADEF为平行四边形，M，N，G分别是AB，AD，EF的中点．
(1)求证：BE∥平面DMF；
(2)求证：平面BDE∥平面MNG.

证明：(1)如图，连接AE，则AE必过DF与GN的交点O，连接MO，则MO为△ABE的中位线，所以BE∥MO，又BE⊄平面DMF，MO⊂平面DMF，所以BE∥平面DMF.
(2)因为N，G分别为平行四边形ADEF的边AD，EF的中点，所以DE∥GN，又DE⊄平面MNG，GN⊂平面MNG，
所以DE∥平面MNG.
又M为AB的中点，
所以MN为△ABD的中位线，
所以BD∥MN，又BD⊄平面MNG，MN⊂平面MNG，
所以BD∥平面MNG，
又DE与BD为平面BDE内的两条相交直线，所以平面BDE∥平面MNG.
[B级　综合练]
11．(多选)如图，正三棱柱ABC­A1B1C1各条棱的长度均相等，D为AA1的中点，M，N分别是线段BB1和线段CC1上的动点(含端点)，且满足BM＝C1N，当M，N运动时，下列结论中正确的是(　　)

A．在△DMN内总存在与平面ABC平行的线段
B．平面DMN⊥平面BCC1B1
C．三棱锥A1­DMN的体积为定值
D．△DMN可能为直角三角形
解析：选ABC.用平行于平面ABC的平面截平面DMN，则交线平行于平面ABC，故A正确；当M，N分别在BB1，CC1上运动时，若满足BM＝C1N，则线段MN必过正方形BCC1B1的中点O，由DO⊥平面BCC1B1可得平面DMN⊥BCC1B1故B正确；当M，N分别在BB1，CC1上运动时，△A1DM的面积不变，点N到平面A1DM的距离不变，所以三棱锥N­A1DM的体积不变，即三棱锥A1­DMN的体积为定值，故C正确；若△DMN为直角三角形，则必是以∠MDN为直角的直角三角形，易证DM＝DN，所以△DMN为等腰直角三角形，所以DO＝OM＝ON，即MN＝2OD，设正三棱柱的棱长为2，则DO＝，MN＝2，因为MN的最大值为BC1＝2，所以MN不可能为2，所以△DMN不可能为直角三角形，故D错误．故选ABC.
12．如图所示，在正方体ABCD­A1B1C1D1中，点E，F，G，P，Q分别为棱AB，C1D1，D1A1，D1D，C1C的中点．则下列叙述中正确的是(　　)

A．直线BQ∥平面EFG
B．直线A1B∥平面EFG
C．平面APC∥平面EFG
D．平面A1BQ∥平面EFG
解析：选B.过点E，F，G的截面如图所示(H，I分别为AA1，BC的中点)，则BQ和平面EFG相交于点Q，故A错误；因为A1B∥HE，A1B⊄平面EFG，HE⊂平面EFG，所以A1B∥平面EFG，故B正确；AP⊂平面ADD1A1，HG⊂平面ADD1A1，延长HG和AP必相交，故平面APC和平面EFG相交，故C错误；平面A1BQ与平面EFG有公共点Q，故平面A1BQ与平面EFG相交，故D错误．故选B.
13．如图所示，四边形EFGH为空间四边形ABCD的一个截面，若截面为平行四边形．

(1)求证：AB∥平面EFGH，CD∥平面EFGH；
(2)若AB＝4，CD＝6，求四边形EFGH周长的取值范围．
解：(1)证明：因为四边形EFGH为平行四边形，
所以EF∥HG.
因为HG⊂平面ABD，EF⊄平面ABD，所以EF∥平面ABD.
又因为EF⊂平面ABC，平面ABD∩平面ABC＝AB，
所以EF∥AB，又因为AB⊄平面EFGH，EF⊂平面EFGH，
所以AB∥平面EFGH.同理可证，CD∥平面EFGH.
(2)设EF＝x(0