2024版新教材高考数学全程一轮总复习课时作业十五导数的概念及其意义导数的运算

　课时作业(十五)　导数的概念及其意义、导数的运算

　一、单项选择题

1．下列导数运算正确的是(　　)

A．(2x2＋3)′＝4x＋3

B．(sin)′＝cos

C．()′＝

D．(2sinx－3cosx)′＝2cosx＋3sinx

2．已知f(x)＝ax3＋3x2＋2，且f′(－1)＝4，则实数a的值为(　　)

A．B．

C．D．

3．函数y＝f(x)的图象如图所示，f′(x)是函数f(x)的导函数，则下列数值排序正确的是(　　)

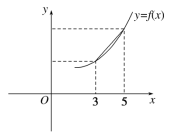
A．2f′(3)<f(5)－f(3)<2f′(5)

B．2f′(3)<2f′(5)<f(5)－f(3)

C．f(5)－f(3)<2f′(3)<2f′(5)

D．2f′(5)<2f′(3)<f(5)－f(3)

4．[2023·河北邯郸月考]已知函数y＝f(x)的图象在点P(3，f(3))处的切线方程是y＝－2x＋7，则f(3)－f′(3)＝(　　)

A．－2B．2

C．－3D．3

5．[2023·江西南昌模拟]曲线f(x)＝2x3－ax在点(1，f(1))处的切线与直线x－y＝0平行，则a＝(　　)

A．1B．2

C．5D．6

6．若曲线y＝lnx＋x2的一条切线的斜率为3，则该切线的方程可能为(　　)

A．3x－y－1＝0B．3x－y＋1＝0

C．3x－y－2＝0D．3x－y－1－ln2＝0

7．[2023·安徽巢湖一中月考]曲线y＝在点(1，b)处的切线方程为kx－y＋6＝0，则k的值为(　　)

A．－1B．－

C．D．1

8．(能力题)设P为曲线y＝ex上一点，Q为曲线y＝lnx上一点，则|PQ|的最小值为(　　)

A．B．1

C．D．2

9．(能力题)[2023·广东湛江模拟]直线y＝x＋t与曲线y＝相切，且与圆x2＋y2＝r2(r>0)相切，则r＝(　　)

A．B．

C．3D．

10．(能力题)若直线y＝kx＋b是曲线y＝ex＋1的切线，也是y＝ex＋2的切线，则k＝(　　)

A．ln2B．－ln2

C．2D．－2

二、多项选择题

11．[2023·河北衡水模拟]下列命题正确的是(　　)

A．若f(x)＝xsinx＋cosx，则f′(x)＝sinx－xcosx＋sinx

B．设函数f(x)＝xlnx，若f′(x0)＝2，则x0＝e

C．已知函数f(x)＝3x2ex，则f′(1)＝12e

D．设函数f(x)的导函数为f′(x)，且f(x)＝x2＋3xf′(2)＋lnx，则f′(2)＝－

12．(能力题)已知函数f(x)＝＋lnx，若f(x)的图象存在两条相互垂直的切线，则a的值可以是(　　)

A．－4B．－3

C．－2D．－1

三、填空题

13．[2023·河南郑州四中月考]曲线y＝xln2x在点(，)处的切线方程为________．

14．(能力题)已知直线x＋y＋a＝0是曲线xy－1＝0的切线，则a＝________________．

四、解答题

15．已知两曲线y＝x3＋ax和y＝x2＋bx＋c都经过点P(1，2)，且在点P处有公切线．

(1)求a，b，c的值；

(2)求公切线与坐标轴围成的三角形的面积．

优生选做题

16．已知函数f(x)＝(x－3)ex，若经过点(0，a)且与曲线y＝f(x)相切的直线有三条，则(　　)

A．－3<a<－eB．a>－e

C．a<－3D．a<－3或a>－e

17．设函数f(x)＝ax－，曲线y＝f(x)在点(2，f(2))处的切线方程为3x－2y－4＝0.

(1)求f(x)的解析式；

(2)证明：曲线f(x)上任一点处的切线与直线x＝0和直线y＝x所围成的三角形的面积为定值，并求此定值．

课时作业（十五）　导数的概念及其意义、导数的运算

1．解析：（2x2＋3）′＝4x，A错误；

（sin）′＝（）′＝0，B错误；

（）′＝，C错误，

（2sinx－3cosx）′＝2cosx＋3sinx，D正确．

故选D.

答案：D

2．解析：∵f（x）＝ax3＋3x2＋2，

∴f′（x）＝3ax2＋6x，

∵f′（－1）＝4，

∴3a－6＝4，

∴a＝.

故选D.

答案：D

3．解析：由图知：f′（3）<<f′（5），即2f′（3）<f（5）－f（3）<2f′（5）.

故选A.

答案：A

4．解析：函数f（x）的图象在点P（3，f（3））处的切线的斜率就是在该点处的导数，即f′（3）就是切线y＝－2x＋7的斜率，所以f′（3）＝－2.

又f（3）＝－2×3＋7＝1，

所以f（3）－f′（3）＝1－（－2）＝3.

故选D.

答案：D

5．解析：由f（x）＝2x3－ax得f′（x）＝6x2－a，

因为曲线f（x）在点（1，f（1））处的切线与直线x－y＝0平行，

所以f′（1）＝6－a＝1即a＝5，

故选C.

答案：C

6．解析：设切线的切点坐标为（x0，y0），y＝lnx＋x2，y′＝＋2x，x0>0，

＝＋2x0＝3，

所以或，所以切点坐标为（1，1）或（，ln＋），

所求的切线方程为3x－y－2＝0或3x－y－－ln2＝0.

故选C.

答案：C

7．解析：由切点（1，b）在曲线上，得b＝；①

由切点（1，b）在切线上，得k－b＋6＝0；②

对曲线求导得y′＝，∴x＝1＝＝k，即4－a＝9k，③

联立①②③，解之得.

故选A.

答案：A

8．解析：y＝ex，y′＝ex，x＝0时，y′＝1，y＝1，所以y＝x＋1是y＝ex图象的一条切线，切点为（0，1），

y＝lnx，y′＝，x＝1时，y′＝1，y＝0，所以y＝x－1是y＝lnx的图象的一条切线，切点为（1，0），

k＝＝－1，

这两条切线平行，两切点连线恰好与切线垂直，

|PQ|的最小值即为两切点间的距离．

所以|PQ|min＝.

故选C.

答案：C

9．解析：设直线y＝x＋t在曲线y＝上的切点为（x0，），

则f′（x0）＝＝，解得x0＝1，故切点坐标为（1，1），

将（1，1）代入直线y＝x＋t中，解得t＝，

所以直线方程为y＝x＋，即x－2y＋1＝0，

又x－2y＋1＝0与圆x2＋y2＝r2（r>0）相切，

则r＝＝.

故选B.

答案：B

10．解析：设直线y＝kx＋b与y＝ex＋2和y＝ex＋1的切点分别为（x1，＋2），（x2，），

则切线方程分别为，

y－（＋2）＝（x－x1），

y－＝（x－x2），

化简得，

y＝x＋＋2－x1

y＝x－x2＋

依题意上述两直线与y＝kx＋b是同一条直线，

所以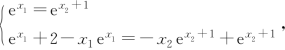，，解得x1＝ln2，

所以k＝＝eln2＝2.

故选C.

答案：C

11．解析：对于选项A，即f′（x）＝sinx＋xcosx－sinx，则选项A不正确；

对于选项B，即f′（x）＝lnx＋1，则f′（x0）＝lnx0＋1＝2，解得x0＝e，则选项B正确；

对于选项C，即f′（x）＝6xex＋3x2ex，则f′（1）＝6e＋3e＝9e，则选项C不正确；

对于选项D，即f′（x）＝2x＋3f′（2）＋，f′（2）＝4＋3f′（2）＋，解得f′（2）＝－，

则选项D正确．

故选BD.

答案：BD

12．解析：∵函数f（x）＝＋lnx，定义域为（0，＋∞），∴f′（x）＝x＋a＋，

∴f′（x）＝x＋a＋≥a＋2，当且仅当x＝时，取等号，

要使f（x）的图象存在两条相互垂直的切线，则∃x1，x2∈（0，＋∞），f′（x1）f′（x2）＝－1，

所以f′（x）＝x＋a＋的值必有一正一负，

当a＝－4时，f′（x）＝x＋a＋≥－2，易知符合题意，

当a＝－3时，f′（x）＝x＋a＋≥－1，易知符合题意，

当a＝－2时，f′（x）＝x＋a＋≥0，不符合题意，

当a＝－1时，f′（x）＝x＋a＋≥1，不符合题意，

所以a的值可以是－4或－3.

故选AB.

答案：AB

13．解析：y＝xln2x，则y′＝ln2x＋1，则k＝y′|x＝＝ln（2×）＋1＝2，

则曲线y＝xln2x在点（，）处的切线方程为

y－＝2，即y＝2x－.

答案：y＝2x－

14．解析：设切点为（x0，y0），由xy－1＝0，可得y＝，

∴y′＝－，∵直线x＋y＋a＝0是切线，

∴＝－＝－1，解得x0＝±1，

当x0＝1时，y0＝＝1，切点（1，1）代入切线方程x＋y＋a＝0，可得a＝－2，

当x0＝－1时，y0＝＝－1，切点（－1，－1）代入切线方程x＋y＋a＝0，可得a＝2，

综上可知，a＝±2.

答案：±2

15．解析：（1）两函数y＝x3＋ax和y＝x2＋bx＋c的导数分别为

y′＝3x2＋a和y′＝2x＋b，

由题意，

解得.

（2）由（1）知公切线方程为y－2＝4（x－1），

即4x－y－2＝0，

令x＝0得y＝－2，令y＝0得x＝，

所以所求面积为S＝×2×＝.

16．解析：f′（x）＝（x－2）ex，设经过点（0，a）且与曲线y＝f（x）相切的切点为，则f′（x0）＝（x0－2）ex0.又切线经过（0，a），故由题意＝（x0－2）ex0有3个解．

化简有a＝（x0－3）ex0－x0（x0－2）ex0，即a＝（－x＋3x0－3）ex0有3个解．

设g（x）＝（－x2＋3x－3）ex，则g′（x）＝（－x2＋x）ex，令g′（x）＝0有x＝0或x＝1，故当x∈（－∞，0）时，g′（x）<0，g（x）单调递减；当x∈（0，1）时，g′（x）>0，g（x）单调递增；当x∈（1，＋∞）时，g′（x）<0，g（x）单调递减．

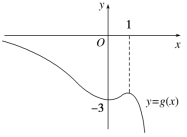
又g（0）＝－3，g（1）＝－e，且g（－1）＝－>g（1），g（2）＝－e2<g（0），故要a＝（－x＋3x0－3）ex0有3个解，则－3<a<－e.

故选A.

答案：A

17．解析：（1）f（x）＝ax－的导数为f′（x）＝a＋，

可得y＝f（x）在x＝2处的切线斜率为a＋，

由切线方程3x－2y－4＝0，可得

解得a＝1，b＝2，则f（x）＝x－.

（2）证明：设P（x0，y0）为曲线上任一点，由y′＝1＋，

可得曲线在点P（x0，y0）处的切线方程为

y－y0＝（1＋）（x－x0），

即y－（x0－）＝（1＋）（x－x0），

令x＝0，得y＝－，从而得切线与直线x＝0的交点坐标为（0，－）；

令y＝x，得y＝x＝2x0，从而得切线与直线y＝x的交点坐标为（2x0，2x0）.

∴点P（x0，y0）处的切线与直线x＝0，y＝x所围成的三角形面积为·|2x0|＝4.故曲线y＝f（x）上任一点处的切线与直线x＝0，y＝x所围成的三角形面积为定值，此定值为4.