





2024版新教材高考数学全程一轮总复习第三章导数及其应用第二节导数与函数的单调性课件
展开【课标标准】 1.结合实例,借助几何直观了解函数的单调性和导数的关系.2.能利用导数研究函数的单调性.3.对于多项式函数,能求不超过三次的多项式函数的单调区间.
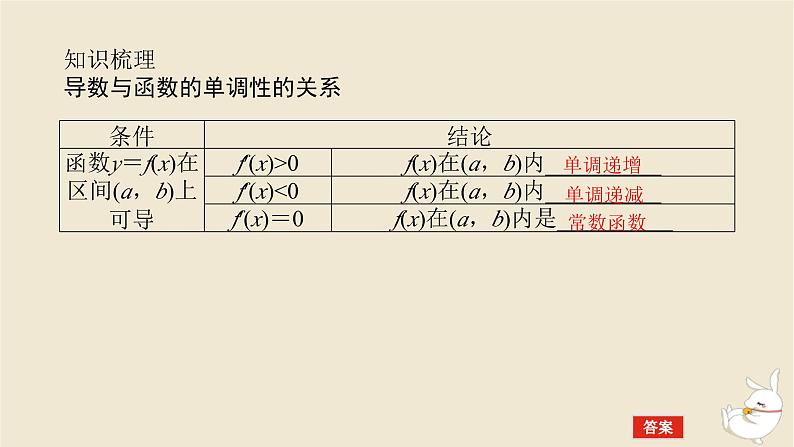
知识梳理导数与函数的单调性的关系
[常用结论]1.若函数f(x)在(a,b)上单调递增,则x∈(a,b)时,f′(x)≥0恒成立;若函数f(x)在(a,b)上单调递减,则x∈(a,b)时,f′(x)≤0恒成立.2.若函数f(x)在(a,b)上存在单调递增区间,则x∈(a,b)时,f′(x)>0有解;若函数f(x)在(a,b)上存在单调递减区间,则x∈(a,b)时,f′(x)<0有解.
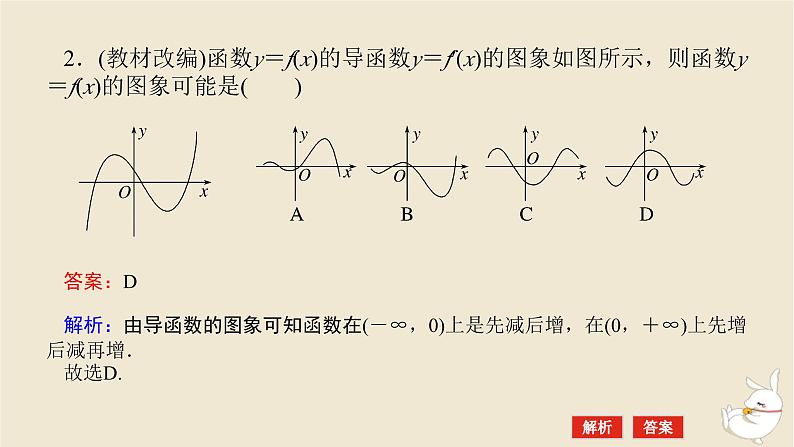
2.(教材改编)函数y=f(x)的导函数y=f′(x)的图象如图所示,则函数y=f(x)的图象可能是( )
解析:由导函数的图象可知函数在(-∞,0)上是先减后增,在(0,+∞)上先增后减再增.故选D.
3.(教材改编)函数y=3x2-2ln x的单调递增区间为___________,单调递减区间为________.
题后师说求函数单调区间的步骤
(2)[2023·河北唐山一中月考]函数f(x)=sin x-x,x∈(0,π)的单调递减区间为________.
题后师说(1)研究含参数的函数的单调性,要依据参数对不等式解集的影响进行分类讨论.(2)若导函数为二次函数式,首先看能否因式分解,再讨论二次项系数的正负及两根的大小;若不能因式分解,则需讨论判别式Δ的正负,二次项系数的正负,两根的大小及根是否在定义域内.
(2)已知定义在R上的函数f(x)满足:xf′(x)+f(x)>0,且f(1)=1,则xf(x)>1的解集为___________.
解析:由题意得,构造g(x)=xf(x),则g′(x)=f(x)+xf′(x)>0,则g(x)在R上为单调递增函数,因为f(1)=1,所以g(1)=1×f(1)=1,所以xf(x)>1可变形为g(x)>g(1),因为g(x)在R上为单调递增函数,所以x>1,则xf(x)>1的解集为{x|x>1}.
题后师说利用单调性比较大小或解不等式,关键是根据题意构造辅助函数,利用构造的函数的单调性比较大小或解不等式.(关于构造函数见后面的专题突破)
(2)已知定义在R上的函数f(x)的导函数为f′(x),且对任意x∈R都有f′(x)>2,f(1)=3,则不等式f(x)-2x-1>0的解集为( )A.(-∞,1) B.(1,+∞)C.(0,+∞) D.(-∞,0)
解析:令g(x)=f(x)-2x-1,则g′(x)=f′(x)-2>0,∴g(x)在(-∞,+∞)上为增函数,又g(1)=f(1)-3=0.∴不等式f(x)-2x-1>0⇔g(x)>g(1),可得x>1.∴不等式f(x)-2x-1>0的解集为(1,+∞).故选B.
角度二 根据单调性求参数的范围例 4 已知函数f(x)=x2-a ln x+1在[1,2]内单调递增,则实数a的取值范围是________.
变式探究1 已知函数f(x)=x2-a ln x+1在[1,2]内存在单调递增区间,则实数a的取值范围是________.
题后师说根据函数的单调性求参数的策略
巩固训练4(1)[2023·河北石家庄模拟]已知函数f(x)=x-a ln x在区间(0,1)上单调递减,则实数a的取值范围是( )A.a>1 B.a≥1 C.a>0 D.a≥0
微专题2 利用f(x)与ex构造例 2(1)已知定义在R上的函数f(x)的导函数为f′(x),对任意x∈R满足f(x)+f′(x)<0,则下列结论一定正确的是( )A.e2f(2)>e3f(3) B.e2f(2)
(2)[2023·辽宁锦州模拟]已知定义在R上的函数f(x)的导函数f′(x),且f(x)
微专题4 同构法构造函数例 4 (1)设a,b都为正数,e为自然对数的底数,若aea+1+be B.b>ea+1C.ab
2024版新教材高考数学全程一轮总复习第三章导数及其应用第一节导数的概念及其意义导数的运算课件: 这是一份2024版新教材高考数学全程一轮总复习第三章导数及其应用第一节导数的概念及其意义导数的运算课件,共44页。PPT课件主要包含了必备知识·夯实双基,关键能力·题型突破,f′x0,切线的斜率,nxn-1,cosx,-sinx,axlna,cf′x,答案C等内容,欢迎下载使用。
2024版新教材高考数学全程一轮总复习第三章导数及其应用第三节导数与函数的极值最值课件: 这是一份2024版新教材高考数学全程一轮总复习第三章导数及其应用第三节导数与函数的极值最值课件,共57页。PPT课件主要包含了必备知识·夯实双基,关键能力·题型突破,f′x0,连续不断,答案C,答案A,答案B,-∞0,-12等内容,欢迎下载使用。
备战2024高考一轮复习数学(理) 第三章 导数及其应用 第二节 导数与函数的单调性课件PPT: 这是一份备战2024高考一轮复习数学(理) 第三章 导数及其应用 第二节 导数与函数的单调性课件PPT,共33页。












