湘教版数学八年级下册同步练习 2.1~2.3滚动训练

这是一份湘教版数学八年级下册同步练习 2.1~2.3滚动训练，共7页。
B[范围:2.1~2.3]一、选择题1.(2020常德)下面中式窗户图形中既是轴对称图形又是中心对称图形的是 (　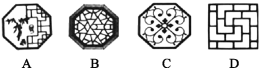　)2.在▱ABCD中,∠A∶∠B∶∠C=3∶6∶3,则∠D的度数为 (　　)A.90° B.67.5° C.112.5° D.120°3.若一个多边形的内角和与外角和之差是720°,则此多边形的边数为 (　　)A.6 B.7 C.8 D.94.如图,在▱ABCD中,AB<BC,对角线AC的垂直平分线交AD于点E,连接CE.若▱ABCD的周长为20 cm,则△CDE的周长为(　　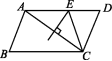)A.20 cm B.40 cm C.15 cm D.10 cm5.下列条件中不能判定四边形ABCD为平行四边形的是 (　　)A.AB∥CD,AD=BC  B.AB∥CD,∠A=∠CC.AD∥BC,AD=BC  D.∠A=∠C,∠B=∠D6.八年级(6)班的一个互助学习小组组长收集并整理了组员们讨论如下问题时所需的条件.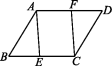如图所示,在四边形ABCD中,点E,F分别在边BC,AD上,　       . 求证:四边形AECF是平行四边形.你能在横线上填上最少且简捷的条件使结论成立吗?条件分别是:①BE=DF;②∠B=∠D;③∠BAE=∠DCF;④四边形ABCD是平行四边形.其中所填条件符合题目要求的是 (　　)A.①②③④ B.①②③ C.①④ D.④二、填空题7.(2020湘西州)若一个多边形的内角和是外角和的2倍,则该多边形的边数是　　　　. 8.(2020甘孜州)如图,在▱ABCD中,过点C作CE⊥AB,垂足为E,若∠EAD=40°,则∠BCE的度数为　　　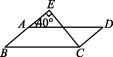　. 9.△ABC与△DEF关于点O成中心对称,且点A,B,C的对称点分别为点D,E,F.若AB=5,AC=3,则EF的取值范围是　　　　. 10.若AC=10 cm,BD=8 cm,AC与BD相交于点O,则当AO=　　　　cm,DO=　　　　cm时,四边形ABCD是平行四边形. 11.将两块相同的含有30°角的三角尺按如图所示的方式摆放在一起,则四边形ABCD为平行四边形,请你写出判断的依据　　　　　　　　　　　　　(写出一种即可). 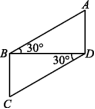三、解答题12.一个多边形的每个内角都相等,并且每个外角都等于它的相邻内角的,求这个多边形的边数及内角和.   13.如图,E为平行四边形ABCD的边CD的中点,连接AE并延长交BC的延长线于点F.(1)求证:AD=CF;(2)若AB=2BC,∠B=70°,求∠F的度数.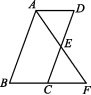图    14.(2020常德期末)如图,在平行四边形ABCD中,O为对角线AC与BD的交点,M,N分别是OA,OC的中点.连接DM,MB,BN,DN.求证:DM∥BN. 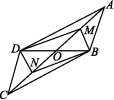   15.如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE⊥AC,垂足为E,连接BE.(1)求证:四边形ABCD是平行四边形;(2)若△ABE是等边三角形,四边形BCDE的面积等于2,求CE的长.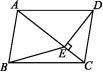   16.如图,▱ABCD的对角线AC与BD相交于点O,点E,F分别在OB和OD上.(1)当BE,DF满足什么条件时,四边形AECF是平行四边形?请说明理由;(2)当∠AEB与∠CFD满足什么条件时,四边形AECF是平行四边形?请说明理由.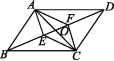  
答案1.C　2.D3. C　∵一个多边形的内角和与外角和之差为720°,多边形的外角和是360°,∴这个多边形的内角和为720°+360°=1080°.设这个多边形的边数为n,则(n-2)·180°=1080°,解得n=8.4.D　5.A6. C　当添加①④时,可得四边形AECF是平行四边形.理由:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC.∵BE=DF,∴AD-DF=BC-BE,即AF=EC.又∵AF∥EC,∴四边形AECF是平行四边形.7. 6 设该多边形的边数为n.根据题意,得(n-2)·180°=360°×2,解得n=6.故这个多边形的边数为6.故答案为6.8. 50° ∵四边形ABCD为平行四边形,∴AD∥BC,∴∠EBC=∠EAD.∵∠EAD=40°,∴∠EBC=40°.∵CE⊥AB,∴∠BCE=50°.故答案为50°.9. 2<EF<8 ∵△ABC与△DEF关于点O成中心对称,且点A,B,C的对称点分别为点D,E,F,AB=5,AC=3,∴DE=5,DF=3,∴EF的取值范围为2<EF<8.10. 5　4 ∵四边形ABCD是平行四边形,∴AO=AC,DO=BD.∵AC=10 cm,BD=8 cm,∴AO=5 cm,DO=4 cm.11.两组对边分别平行的四边形是平行四边形(答案不唯一)12.解:设这个多边形的一个外角的度数为x°.由题意得x=(180-x),解得x=36.360÷36=10,(10-2)×180°=1440°.所以这个多边形的边数为10,内角和为1440°.13.解:(1)证明:∵E是边CD的中点,∴DE=CE.∵四边形ABCD是平行四边形,∴AD∥BF,∴∠D=∠ECF.在△ADE和△FCE中,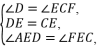∴△ADE≌△FCE(ASA),∴AD=CF.(2)∵四边形ABCD是平行四边形,∴AD=BC.∵△ADE≌△FCE,∴AD=FC,∴BC=FC,∴BF=2BC.又∵AB=2BC,∴BF=AB,∴∠F=(180°-∠B)=×(180°-70°)=55°.14.证明:∵四边形ABCD是平行四边形,∴AO=CO,BO=DO.又∵M,N分别是OA,OC的中点,∴MO=NO,∴四边形BMDN是平行四边形,∴DM∥BN.15.解:(1)证明:∵AB∥CD,∴∠DAB+∠ADC=∠ABC+∠BCD=180°.∵∠ABC=∠ADC,∴∠DAB=∠BCD,∴四边形ABCD是平行四边形.(2)∵△ABE是等边三角形,∴∠BAC=60°.∵AB∥CD,∴∠BAC=∠ACD=60°.在Rt△CDE中,设CD的长为a,则CE=a,由勾股定理,可得DE=a,∴S△CED=a2.∵△CED与△CEB是同底等高的三角形,∴S△CED=S△CEB.又∵S四边形BCDE=S△CED+S△CEB=2,∴a2+a2=2,∴a=2(负值已舍去),∴CE=a=.16.解:(1)当BE=DF时,四边形AECF是平行四边形.理由:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABE=∠CDF.在△ABE与△CDF中,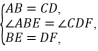∴△ABE≌△CDF(SAS),∴AE=CF.同理,AF=CE,∴四边形AECF是平行四边形.(2)当∠AEB=∠CFD时,四边形AECF是平行四边形.理由:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABE=∠CDF.又∵∠AEB=∠CFD,∴△ABE≌△CDF(AAS),∴AE=CF.∵∠AEB=∠CFD,∴∠AEO=∠CFO,∴AE∥CF.又∵AE=CF,∴四边形AECF是平行四边形.