二次函数综合题教学设计-中考数学复习

九年级数学“生·活”课堂教学

课题：二次函数综合题                主备人：                   审核人：

班级：                             姓 名：                    完成时间：         分钟

一、【要点归纳】

二次函数综合题是中考必考的题型，一般出现在压轴题位置，考查到二次函数的图像与性质、几何图形的判定、性质，通常会考查到线段最值、定值、面积定值及最值、周长定值及最值、直线的关系、全等三角形的判定与性质、相似三角形的判定与性质、特殊三角形的存在性问题、特殊四边形的存在性问题、抛物线与圆等，考查的范围比较广。

类型一：二次函数与线段有关的问题            类型二：二次函数与图形面积有关的问题

类型三：二次函数与角度有关的问题            类型四：二次函数与特殊三角形判定有关的问题

类型五：二次函数与特殊四边形判定有关的问题  类型六：二次函数与圆有关的问题

二、【自学自测】

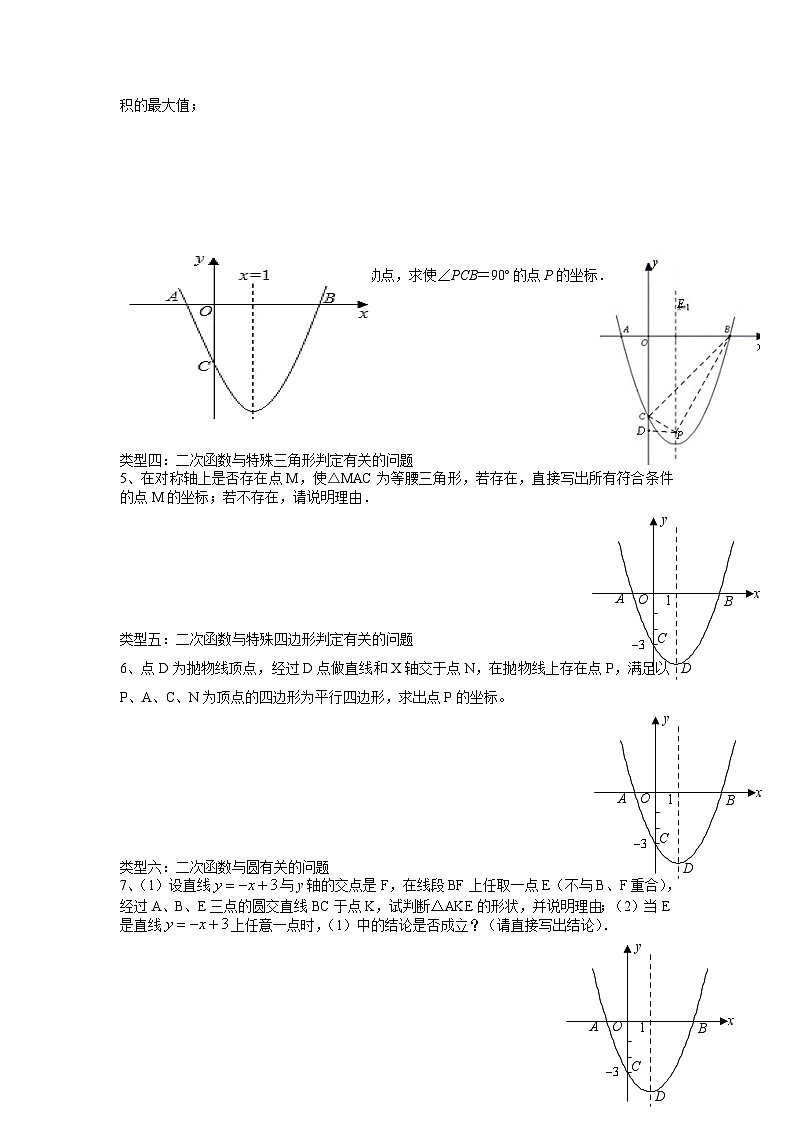
问题1、如图，已知抛物线y1＝ax2+bx+c（a≠0）的对称轴为x＝1，且抛物线经过A（－1，0）、

C（0，－3）两点，与x轴交于另一点B．经过点B、C的直线为y2=mx+n。

1、求直线BC及抛物线所对应的函数关系式；

2、填空：

⑴不等式ax2+bx+c＞ mx+n的结集为                   。

⑵不等式ax2+bx+c＞-3的解集为                       。

⑶当0＜x＜3时，y的取值范围是                       。

三、【研学活动】

类型一：二次函数与线段有关的问题

1、在抛物线的对称轴x＝1上求一点M，使点M到点A的距离与到点C的距离之和最小，并求此时点M

的坐标；

2、P是线段BC上的一个动点，过P点作y轴的平行线交抛物线于E点，求线段PE长度的最大值；

类型二：二次函数与图形面积有关的问题

3、P是线段BC上的一个动点，过P点作y轴的平行线交抛物线于E点，求线段△EBC面积的最大值；

类型三：二次函数与角度有关的问题   

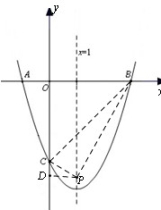
4、设点P为抛物线的对称轴x=1上的一动点，求使∠PCB＝90º的点P的坐标．

类型四：二次函数与特殊三角形判定有关的问题

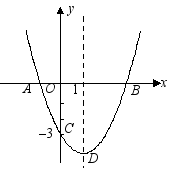
5、在对称轴上是否存在点M，使△MAC为等腰三角形，若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．

类型五：二次函数与特殊四边形判定有关的问题

6、点D为抛物线顶点，经过D点做直线和X轴交于点N，在抛物线上存在点P，满足以P、A、C、N为顶点的四边形为平行四边形，求出点P的坐标。

类型六：二次函数与圆有关的问题

7、（1）设直线与y轴的交点是F，在线段BF上任取一点E（不与B、F重合），经过A、B、E三点的圆交直线BC于点K，试判断△AKE的形状，并说明理由；（2）当E是直线上任意一点时，（1）中的结论是否成立？（请直接写出结论）．

课堂练习

1、在抛物线上求点Q，使△BCQ为直角三角形．

2、在二次函数的图象上是否存在点P，使,若存在，求出P点的坐标；若不存在，请说明理由；

【检学综练】

1、点K（2，m）在抛物线上一点，在抛物线上存在点另一点P，且∠KBP=45°，求点P的坐标．

2、将二次函数的图象在轴下方的部分沿轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线与此图象有两个公共点时，的取值范围．

2、若P为抛物线在第四象限上的一个动点，过点P作PQ∥AC交x轴于点Q．

（1）当点P的坐标为多少时，四边形PQAC是平行四边形；

（2）当点P的坐标为多少时，四边形PQAC是等腰梯形（直接写出结果，不写求解过程）．

4、若点在线段BA上以每秒1个单位长度的速度从B向A运动（不与重合），同时，点在射线上以每秒2个单位长度的速度从向运动．设运动时间为秒，请写出的面积与的函数关系式，并求出点运动多少时间时，的面积最大，最大面积是多少？