


石家庄市重点中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案
展开石家庄市重点中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列几组数中,能作为直角三角形三边长度的是( )
A.2,3,4 B.4,5,6 C.6,8,11 D.5,12,13
2.已知![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的根,则
的根,则![]() 的值是( )
的值是( )
A.-1 B.3 C.1 D.-3
3.某老师为了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,绘成如图所示的条形统计图,则这10名学生周末学均时间是( )
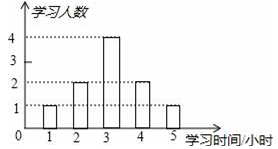
A.4 B.3 C.2 D.1
4.下面的多边形中,内角和与外角和相等的是( )
A.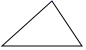 B.
B.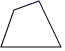
C.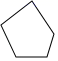 D.
D.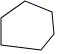
5.炎炎夏日,甲安装队为A小区安装60台空调,乙安装队为B小区安装50台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装2台.设乙队每天安装x台,根据题意,下面所列方程中正确的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.小明发现下列几组数据能作为三角形的边:①3,4,5; ②5,12,13;③12,15,20;④8,24,25;其中能作为直角三角形的三边长的有( )组
A.1 B.2 C.3 D.4
7.如图,在![]() 中,点
中,点![]() 是对角线
是对角线![]() ,
,![]() 的交点,点
的交点,点![]() 是边
是边![]() 的中点,且
的中点,且![]() ,则
,则![]() 的长为( )
的长为( )
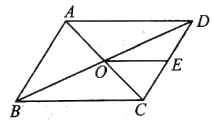
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若一次函数y=kx+17的图象经过点(-3,2),则k的值为( )
A.-6 B.6 C.-5 D.5
9.如图,![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点O,
相交于点O,![]() 交
交![]() 于点E,连接
于点E,连接![]() ,若
,若![]() 的周长为28,则
的周长为28,则![]() 的周长为( )
的周长为( )
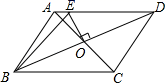
A.28 B.24 C.21 D.14
10.代数式2x,![]() ,x+
,x+![]() ,
,![]() 中分式有( )
中分式有( )
A.1个 B.2个 C.3个 D.4个
11.若x2+mxy+y2是一个完全平方式,则m=( )
A.2 B.1 C.±1 D.±2
12.如图,在平行四边形ABCD中,对角线AC、BD交于点O,E是CD的中点,若OE=2,则AD的长为( )
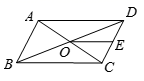
A.2 B.3
C.4 D.5
二、填空题(每题4分,满分20分,将答案填在答题纸上)
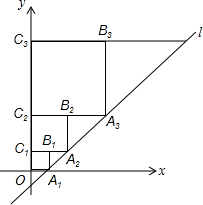
13.在平面直角坐标系中,直线l:![]() 与x轴交于点
与x轴交于点![]() ,如图所示依次作正方形
,如图所示依次作正方形![]() 、正方形
、正方形![]() 、…、正方形
、…、正方形![]() ,使得点
,使得点![]() …在直线l上,点
…在直线l上,点![]() …在y轴正半轴上,则点
…在y轴正半轴上,则点![]() 的横坐标是__________________。
的横坐标是__________________。
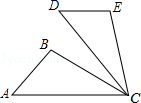
14.如图,△ACB≌△DCE,∠ACD=50°,则∠BCE的度数为_____.
15.观察下列各式:(x-1)(x+1)=x2-1;(x-1)(x2+x+1)=x3-1;(x-1)(x3+x2+x+1)=x4-1,根据前面各式的规律可得(x-1)(xn+xn-1+…+x+1)=______(其中n为正整数).
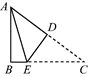
16.如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为____.
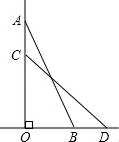
17.如图,一架15m长的梯子AB斜靠在一竖直的墙OA上,这时梯子的顶端A离地面距离OA为12m,如果梯子顶端A沿墙下滑3m至C点,那么梯子底端B向外移至D点,则BD的长为___m.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
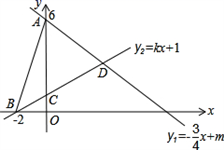
18.(5分)如图,直线l1:y1=−![]() x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
(1)求两直线交点D的坐标;
(2)求△ABD的面积;
(3)根据图象直接写出y1>y2时自变量x的取值范围.
19.(5分)因式分解:
(1)m2n﹣2mn+n;
(2)x2+3x(x﹣3)﹣9
20.(8分)如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 和点
和点![]() .
.
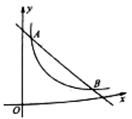
(1)求![]() ,
,![]() 的值;
的值;
(2)根据图象判断,当不等式![]() 成立时,
成立时,![]() 的取值范围是什么?
的取值范围是什么?
21.(10分)计算题:
(1)解不等式组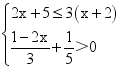
(2)先化筒,再求值(![]() )
)![]() ,其中m=
,其中m=![]()
(3)解方程![]() =1-
=1-![]()
22.(10分)一种五米种子的价格为5元/kg,A如果一次购买2kg以上的种子,超过2kg部分的种子价格打八折.
(1)填写表:
购买量/kg | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | … |
付款金额/元 |
|
|
|
|
|
|
|
|
|
(2)写出付款金额关于购买量的函数解析式,并画出函数图象.
23.(12分)为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.
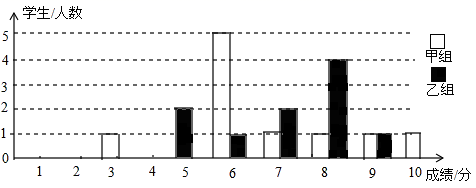
(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 |
| 3.41 | 90% | 20% |
乙组 |
| 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、B
3、B
4、B
5、D
6、B
7、C
8、D
9、D
10、A
11、D
12、C
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、50°
15、xn+1-1
16、1
17、1
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)D点坐标为(4,3)(1)15;(3)x<4
19、 (1) n(m-1)1;(1)(x-3)(4x+3)
20、(1)![]() ,
, ![]() ;(2)
;(2)![]() 或
或![]() .
.
21、(1)-1≤x<![]() ;(2)-5;(3)x=
;(2)-5;(3)x=![]() 是原分式方程的根.
是原分式方程的根.
22、(1)2.5、5、7.5、10、12、14、16、18;(2)![]()
23、(1)6;7.1;(2)甲;(3)乙组的平均分,中位数高于甲组,方差小于甲组,故乙组成绩好于甲组
郑州市重点中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案: 这是一份郑州市重点中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案,共6页。试卷主要包含了下列语句正确的是等内容,欢迎下载使用。
山东省重点中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案: 这是一份山东省重点中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案,共8页。试卷主要包含了已知,则等内容,欢迎下载使用。
安徽省重点中学2022-2023学年数学七年级第二学期期末学业质量监测模拟试题含答案: 这是一份安徽省重点中学2022-2023学年数学七年级第二学期期末学业质量监测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。












