


湖南省永州市祁阳县2022-2023学年数学七年级第二学期期末学业质量监测模拟试题含答案
展开湖南省永州市祁阳县2022-2023学年数学七年级第二学期期末学业质量监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.在 2008 年的一次抗震救灾大型募捐活动中,文艺工作者积极向灾区捐款.其中 10 人 的捐款分别是:5 万,8 万,10 万,10 万,10 万,20 万,20 万,30 万,50 万,100 万.这组数据的众数和中位数分别是( )
A.10 万,15 万 B.10 万,20 万 C.20 万,15 万 D.20 万,10 万
2.如图,在□ABCD中,点E、F分别在边AB、DC上,下列条件不能使四边形EBFD是平行四边形的条件是( )
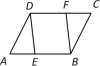
A.DE=BF B.AE=CF C.DE∥FB D.∠ADE=∠CBF
3.一个多边形的内角和等于1260°,则从此多边形一个顶点引出的对角线有( )
A.4条 B.5条 C.6条 D.7条
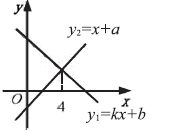
4.一次函数![]() 与
与![]() 的图象如图所示,有下列结论:①
的图象如图所示,有下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 其中正确的结论有( )
其中正确的结论有( )
A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个
个
5.下列等式一定成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.函数y=![]() 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A.x≥1 B.x>1 C.x≥1且x≠2 D.x≠2
7.下列各曲线中能表示y是x的函数的是( )
A.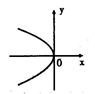 B.
B.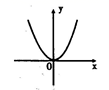 C.
C.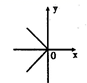 D.
D.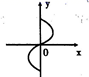
8.下列说法:①实数和数轴上的点是一一对应的;②无理数是开方开不尽的数;③负数没有立方根;④16的平方根是![]() ,用式子表示是
,用式子表示是![]() .其中错误的个数有( )
.其中错误的个数有( )
A.0个 B.1个 C.2个 D.3个
9.如图,把一个矩形纸片ABCD沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′为( )。
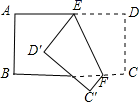
A.70° B.65° C.50° D.25°
10.若函数![]() 的图象与坐标轴有三个交点,则b的取值范围是
的图象与坐标轴有三个交点,则b的取值范围是![]()
![]()
A.![]() 且
且![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.菱形的周长为8cm,一条对角线长2cm,则另一条对角线长为 cm.。
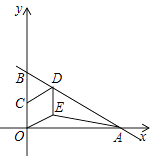
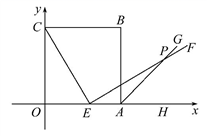
12.如图,直线![]() 与x轴、y轴分别交于A,B两点,C是OB的中点,D是AB上一点,四边形OEDC是菱形,则△OAE的面积为________.
与x轴、y轴分别交于A,B两点,C是OB的中点,D是AB上一点,四边形OEDC是菱形,则△OAE的面积为________.
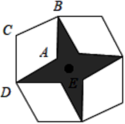
13.将菱形![]() 以点
以点![]() 为中心,按顺时针方向分别旋转
为中心,按顺时针方向分别旋转![]() ,
,![]() ,
,![]() 后形成如图所示的图形,若
后形成如图所示的图形,若![]() ,
,![]() ,则图中阴影部分的面积为__.
,则图中阴影部分的面积为__.
14.将点![]() 向右平移4个单位,再向下平移3个单位,则平移后点的坐标是__________.
向右平移4个单位,再向下平移3个单位,则平移后点的坐标是__________.
15.若分式![]() 的值为
的值为![]() ,则
,则![]() 的值为_______.
的值为_______.
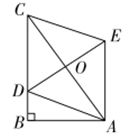
16.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,以
上,以![]() 为对角线的所有
为对角线的所有![]() 中,
中,![]() 的最小值是____.
的最小值是____.
三、解下列各题(本大题共8小题,共72分)
17.(8分)(如图①,将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点 M处,点C落在点N处,MN与CD交于点P, 连接EP.
⑴如图②,若M为AD边的中点,①△AEM的周长=_________cm;②求证:EP=AE+DP;
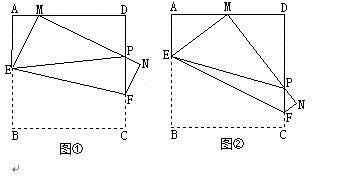
⑵随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.
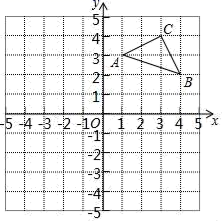
18.(8分)如图,在平面直角坐标系内,已知△ABC的三个顶点坐标分别为A(1,3)、B(4,2)、C(3,4).
(1)将△ABC沿水平方向向左平移4个单位得△A1B1C1,请画出△A1B1C1;
(2)画出△ABC关于原点O成中心对称的△A2B2C2;
(3)若△A1B1C1与△A2B2C2关于点P成中心对称,则点P的坐标是
19.(8分)为了满足学生的物质需求,我市某中学到红旗超市准备购进甲、乙两种绿色袋装食品.其中甲、乙两种绿色袋装食品的进价和售价如下表:
| 甲 | 乙 |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于5200元,且不超5280元,问该红旗超市有几种进货方案?
(3)在(2)的条件下,该红旗超市准备对甲种袋装食品进行优惠促销活动,决定对甲种袋装食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?
20.(8分)如图,边长为5的正方形OABC的顶点O在坐标原点处,点A,C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.
(1)求证:CE=EP.
(2)若点E的坐标为(3,0),在y轴上是否存在点M,使得四边形BMEP是平行四边形?若存在,求出点M的坐标;若不存在,说明理由.
21.(8分)四边形ABCD是边长为4的正方形,点E在边AD所在的直线上,连接CE,以CE为边,作正方形CEFG(点D,点F在直线CE的同侧),连接BF,
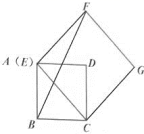

图1 图2
(1)如图1,当点E与点A重合时,则![]() _____;
_____;
(2)如图2,当点E在线段AD上时,![]() ,
,
①求点F到AD的距离;
②求BF的长.
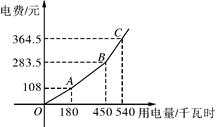
22.(10分)为了响应国家节能减排的号召,鼓励市民节约用电,我市从2012年7月1日起,居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况如图的折线图,请根据图象回答下列问题;
(1)当用电量是180千瓦时时,电费是__________元;
(2)第二档的用电量范围是__________;
(3)“基本电价”是__________元/千瓦时;
(4)小明家8月份的电费是1.5元,这个月他家用电多少千瓦时?
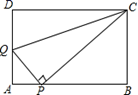
23.(10分)如图,在![]() ABCD中,点P是AB边上一点(不与A,B重合),过点P作PQ⊥CP,交AD边于点Q,且
ABCD中,点P是AB边上一点(不与A,B重合),过点P作PQ⊥CP,交AD边于点Q,且![]() ,连结
,连结![]() .
.
(1)求证:四边形![]() 是矩形;
是矩形;
(2)若CP=CD,AP=2,AD=6时,求![]() 的长.
的长.
24.(12分)一水果店主分两批购进某一种水果,第一批所用资金为2400元,因天气原因,水果涨价,第二批所用资金是2700元,但由于第二批单价比第一批单价每箱多10元,以致购买的数量比第一批少25%.
(1)该水果店主购进第一批这种水果的单价是多少元?
(2)该水果店主计两批水果的售价均定为每箱40元,实际销售时按计划无损耗售完第一批后,发现第二批水果品质不如第一批,于是该店主将售价下降a%销售,结果还是出现了20%的损耗,但这两批水果销售完后仍赚了不低于1716元,求a的最大值.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、A
3、C
4、B
5、B
6、C
7、B
8、D
9、C
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、![]()
13、![]()
14、(3,-1)
15、![]()
16、6
三、解下列各题(本大题共8小题,共72分)
17、(1)①6 ,②见解析;(2)△PDM的周长保持不变,理由见解析.
18、(1)见解析(2)见解析(3)(﹣2,0)
19、(1)![]() ;(2)共有17种方案;(3)当
;(2)共有17种方案;(3)当![]() 时,
时,![]() 有最大值,即此时应购进甲种绿色袋装食品240袋,表示出乙种绿色袋装食品560袋.
有最大值,即此时应购进甲种绿色袋装食品240袋,表示出乙种绿色袋装食品560袋.
20、(1)证明见解析;(2)存在点M的坐标为(0,2).
21、 (1)![]() ;(2)①点F到AD的距离为1;②BF=
;(2)①点F到AD的距离为1;②BF=![]() .
.
22、(1)128;
(2)182<x≤442;
(3)2.6;
(4)这个月他家用电422千瓦时.
23、(1)详见解析;(2)![]()
24、(1)水果店主购进第一批这种水果的单价是20元;(2)a的最大值是1.
2023-2024学年湖南省永州市祁阳县数学九上期末统考模拟试题含答案: 这是一份2023-2024学年湖南省永州市祁阳县数学九上期末统考模拟试题含答案,共8页。
2023-2024学年湖南省永州市双牌县数学八年级第一学期期末学业质量监测模拟试题含答案: 这是一份2023-2024学年湖南省永州市双牌县数学八年级第一学期期末学业质量监测模拟试题含答案,共7页。
湖南省邵阳市新邵县2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案: 这是一份湖南省邵阳市新邵县2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案,共8页。试卷主要包含了方程的解是等内容,欢迎下载使用。












