


湖北省黄冈市东坡中学2022-2023学年七年级数学第二学期期末达标检测试题含答案
展开湖北省黄冈市东坡中学2022-2023学年七年级数学第二学期期末达标检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.在下列图形中,既是中心对称图形又是轴对称图形的是![]()
![]()
A. B.
B. C.
C. D.
D.
2.函数![]() 与
与![]() 在同一坐标系中的图象可能是( )
在同一坐标系中的图象可能是( )
A.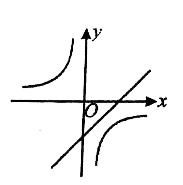 B.
B.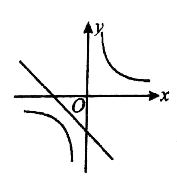
C.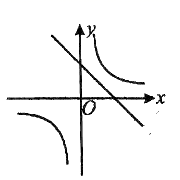 D.
D.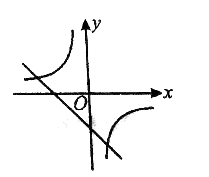
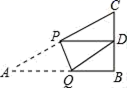
3.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为PQ,则线段BQ的长度为( )
A.![]() B.
B.![]() C.4 D.5
C.4 D.5
4.若三角形的各边长分别是8cm、10cm和16cm,则以各边中点为顶点的三角形的周长为( )
A.34cm B.30cm C.29cm D.17cm
5.某交警在一个路口统计的某时段来往车辆的车速情况如表:
车速(km/h) | 48 | 49 | 50 | 51 | 52 |
车辆数(辆) | 4 | 6 | 7 | 2 | 1 |
则上述车速的中位数和众数分别是( )
A.49,50 B.49.5,7 C.50,50 D.49.5,50
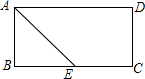
6.在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
A.2和3 B.3和2 C.4和1 D.1和4
7.为了了解中学课堂教学质量,我市教体局去年对全市中学教学质量进行调查![]() 方法是通过考试
方法是通过考试![]() 参加考试的为全市八年级学生
参加考试的为全市八年级学生![]() ,从中随机抽取600名学生的英语成绩进行分析
,从中随机抽取600名学生的英语成绩进行分析![]() 对于这次调查,以下说法不正确的是( )
对于这次调查,以下说法不正确的是( )
A.调查方法是抽样调查 B.全市八年级学生是总体
C.参加考试的每个学生的英语成绩是个体 D.被抽到的600名学生的英语成绩是样本
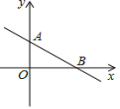
8.如图,在平面直角坐标系中,一次函数![]() 经过
经过![]() ,
,![]() 两点,则不等式
两点,则不等式![]() 的解是
的解是![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.如图,![]() 为
为![]() 外一点,且
外一点,且![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() 的度数为( )
的度数为( )
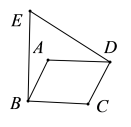
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.当分式![]() 的值为0时,x的值为( )
的值为0时,x的值为( )
A.0 B.3 C.﹣3 D.±3
二、填空题(本大题共有6小题,每小题3分,共18分)
11.在比例尺1∶8000000的地图上,量得太原到北京的距离为6.4厘米,则太原到北京的实际距离为公里。
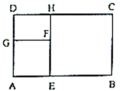
12.如图,在矩形![]() 中,不重叠地放上两张面积分别是
中,不重叠地放上两张面积分别是![]() 和
和![]() 的正方形纸片
的正方形纸片![]() 和
和![]() .矩形
.矩形![]() 没被这两个正方形盖住的面积是________;
没被这两个正方形盖住的面积是________;
13.已知一次函数![]() 的图象经过第一、二、四象,请你写出一个满足条件的
的图象经过第一、二、四象,请你写出一个满足条件的![]() 值__________.
值__________.
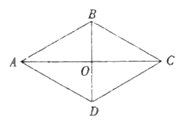
14.如图,菱形ABCD的周长是20,对角线AC、BD相交于点O.若BO=3,则菱形ABCD的面积为______.
15.当![]() ______时,分式方程
______时,分式方程![]() 会产生增根.
会产生增根.
16.已知直线y=kx+b和直线y=-3x平行,且过点(0,-3),则此直线与x轴的交点坐标为________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)某校要从甲、乙两名同学中挑选一人参加创新能力大赛,在最近的五次选拔测试中, 他俩的成绩分别如下表,请根据表中数据解答下列问题:
| 第 1 次 | 第 2 次 | 第 3 次 | 第 4 次 | 第 5 次 | 平均分 | 众数 | 中位数 | 方差 |
甲 | 60 分 | 75 分 | 100 分 | 90 分 | 75 分 | 80 分 | 75 分 | 75 分 | 190 |
乙 | 70 分 | 90 分 | 100 分 | 80 分 | 80 分 |
| 80 分 | 80 分 |
|
(1)把表格补充完整:
(2)在这五次测试中,成绩比较稳定的同学是多少;若将 80 分以上(含 80 分) 的成绩视为优秀,则甲、乙两名同学在这五次测试中的优秀率分别是多少;
(3)历届比赛表明,成绩达到80分以上(含 80分)就很可能获奖,成绩达到 90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
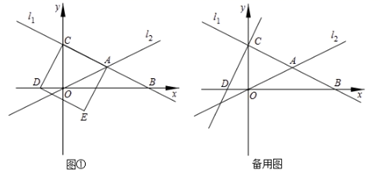
18.(8分)如图①,在平面直角坐标系中,直线![]() :
:![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,且与直线
,且与直线![]() :
:![]() 交于点
交于点![]() ,以线段
,以线段![]() 为边在直线
为边在直线![]() 的下方作正方形
的下方作正方形![]() ,此时点
,此时点![]() 恰好落在
恰好落在![]() 轴上.
轴上.
(1)求出![]() 三点的坐标.
三点的坐标.
(2)求直线![]() 的函数表达式.
的函数表达式.
(3)在(2)的条件下,点![]() 是射线
是射线![]() 上的一个动点,在平面内是否存在点
上的一个动点,在平面内是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
19.(8分)阅读下列材料:
关于x的方程:![]() 的解是
的解是![]() ,
,![]() ;
;![]() 即
即![]() 的解是
的解是![]() ;
;![]() 的解是
的解是![]() ,
,![]() ;
;![]() 的解是
的解是![]() ,
,![]() ;
;![]()
![]() 请观察上述方程与解的特征,比较关于x的方程
请观察上述方程与解的特征,比较关于x的方程![]() 与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
![]() 由上述的观察、比较、猜想、验证,可以得出结论:
由上述的观察、比较、猜想、验证,可以得出结论:
如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这个结论解关于x的方程:![]() .
.
20.(8分)菱形![]() 中,
中,![]() ,
,![]() 是对角线,点
是对角线,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上两个点,且满足
上两个点,且满足![]() ,连接
,连接![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)如图1,求![]() 的度数;
的度数;
(2)如图2,作![]() 于
于![]() 点,求证:
点,求证:![]() ;
;
(3)在满足(2)的条件下,且点![]() 在菱形内部,若
在菱形内部,若![]() ,
,![]() ,求菱形
,求菱形![]() 的面积.
的面积.
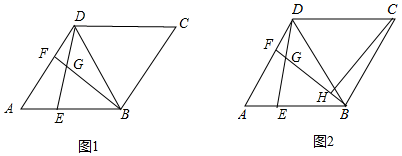
21.(8分) “西瓜足解渴,割裂青瑶肤”,西瓜为夏季之水果,果肉味甜,能降温去暑;种子含油,可作消遣食品;果皮药用,有清热、利尿、降血压之效.某西瓜批发商打算购进“黑美人”西瓜与“无籽”西瓜两个品种的西瓜共70000千克.
(1)若购进“黑美人”西瓜的重量不超过“无籽”西瓜重量的![]() 倍,求“黑美人”西瓜最多购进多少千克?
倍,求“黑美人”西瓜最多购进多少千克?
(2)该批发商按(1)中“黑美人”西瓜最多重量购进,预计“黑美人”西瓜售价为4元/千克;“无籽”西瓜售价为5元/千克,两种西瓜全部售完.由于存储条件的影响,“黑美人”西瓜与“无籽”西瓜分别有![]() 与
与![]() 的损坏而不能售出.天气逐渐炎热,西瓜热卖,“黑美人”西瓜的销售价格上涨
的损坏而不能售出.天气逐渐炎热,西瓜热卖,“黑美人”西瓜的销售价格上涨![]() ,“无籽”西瓜的销售价格上涨
,“无籽”西瓜的销售价格上涨![]() ,结果售完之后所得的总销售额比原计划下降了3000元,求
,结果售完之后所得的总销售额比原计划下降了3000元,求![]() 的值.
的值.
22.(10分)阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
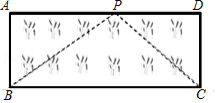
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
23.(10分)在坐标系下画出函数![]() 的图象,
的图象,
(1)正比例函数![]() 的图象与
的图象与![]() 图象交于A,B两点,A在B的左侧,画出
图象交于A,B两点,A在B的左侧,画出![]() 的图象并求A,B两点坐标
的图象并求A,B两点坐标
(2)根据图象直接写出![]() 时自变量x的取值范围
时自变量x的取值范围
(3)![]() 与x轴交点为C,求
与x轴交点为C,求![]() 的面积
的面积
24.(12分)解下列方程式:
(1)x2﹣3x+1=1.
(2)x2+x﹣12=1.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、D
3、C
4、D
5、D
6、B
7、B
8、D
9、C
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、512
12、![]()
13、答案不唯一
14、24
15、1
16、 (−1,0).
三、解下列各题(本大题共8小题,共72分)
17、(1)84,104;(2)乙;40%,80%;(3)我认为选乙参加比较合适.
18、(1)![]()
![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() ,
,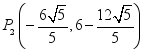 ,
,![]() .
.
19、![]() 猜想
猜想![]() 的解是
的解是![]() ,
,![]() .验证见解析;
.验证见解析;![]() ,
,![]() .
.
20、 (1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
21、(1)最多![]() (2)
(2)![]()
22、 (1)-2,1;(2)x=3;(3)4m.
23、(1)图象详见解析,A(![]() ,
,![]() ),B(8,4);(2)x≤
),B(8,4);(2)x≤![]() 或x>8;(3)
或x>8;(3)![]() .
.
24、(1)x=![]() ;(2)x=﹣4或x=3.
;(2)x=﹣4或x=3.
湖北省黄冈市东坡中学2023-2024学年数学九上期末学业质量监测试题含答案: 这是一份湖北省黄冈市东坡中学2023-2024学年数学九上期末学业质量监测试题含答案,共8页。
2023-2024学年湖北省黄冈市名校数学九上期末达标检测试题含答案: 这是一份2023-2024学年湖北省黄冈市名校数学九上期末达标检测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
湖北省黄冈市东坡中学2023-2024学年数学八上期末联考模拟试题含答案: 这是一份湖北省黄冈市东坡中学2023-2024学年数学八上期末联考模拟试题含答案,共7页。试卷主要包含了已知且,那么等于,下列分式中,是最简分式的是,将多项式分解因式,结果正确的是等内容,欢迎下载使用。












