


河南省新乡市长垣市2022-2023学年数学七年级第二学期期末联考模拟试题含答案
展开河南省新乡市长垣市2022-2023学年数学七年级第二学期期末联考模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知正比例函数y=(m﹣1)x的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2,那么m的取值范围是( )
A.m<1 B.m>1 C.m<2 D.m>0
2.电视塔越高,从塔顶发射出的电磁波传播得越远,从而能收看到电视节目的区域就越广.电视塔高![]() (单位:
(单位:![]() )与电视节目信号的传播半径
)与电视节目信号的传播半径![]() (单位:
(单位:![]() )之间存在近似关系
)之间存在近似关系![]() ,其中
,其中![]() 是地球半径.如果两个电视塔的高分别是
是地球半径.如果两个电视塔的高分别是![]()
![]() ,
,![]()
![]() ,那么它们的传播半径之比是
,那么它们的传播半径之比是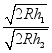 ,则式子
,则式子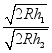 化简为( )
化简为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.有一个直角三角形的两边长分别为3和4,则第三边的长为( )
A.5 B.![]() C.
C.![]() D.5或
D.5或![]()
4.已知矩形的面积为36cm2,相邻的两条边长为xcm和ycm,则y与x之间的函数图像大致是
A.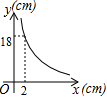 B.
B.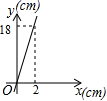 C.
C.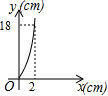 D.
D.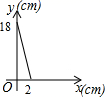
5.一次函数![]() 满足
满足![]() ,且
,且![]() 随
随![]() 的增大而减小,则此函数的图象不经过( )
的增大而减小,则此函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
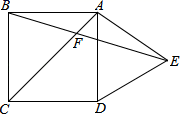
A.75° B.60° C.55° D.45°
7.已知点![]() 的坐标是
的坐标是![]() ,则点
,则点![]() 关于
关于![]() 轴的对称点的坐标是( )
轴的对称点的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.对于函数![]() 有以下四个结论,其中正确的结论是( )
有以下四个结论,其中正确的结论是( )
A.函数图象必经过点![]() B.函数图象经过第一、二、三象限
B.函数图象经过第一、二、三象限
C.函数值y随x的增大而增大 D.当![]() 时,
时,![]()
9.去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数![]() (单位:千克)及方差
(单位:千克)及方差![]() (单位:千克
(单位:千克![]() )如下表所示:
)如下表所示:
| 甲 | 乙 | 丙 | 丁 |
| 24 | 24 | 23 | 20 |
| 2.1 | 1.9 | 2 | 1.9 |
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是( )
A.甲 B.乙 C.丙 D.丁
10.如图,在平面直角坐标系中,已知正方形ABCO,A(0,3),点D为x轴上一动点,以AD为边在AD的右侧作等腰Rt△ADE,∠ADE=90°,连接OE,则OE的最小值为( )
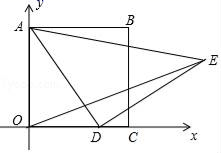
A.![]() B.
B.![]() C.2
C.2![]() D.3
D.3![]()
11.若![]() ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.在同一直角坐标系中,若直线y=kx+3与直线y=-2x+b平行,则( )
A.k=-2,b≠3 B.k=-2,b=3 C.k≠-2,b≠3 D.k≠-2,b=3
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.化简:![]() +
+![]() =___.
=___.
14.在一列数2,3,3,5,7中,他们的平均数为__________.
15.长、宽分别为a、b的矩形,它的周长为14,面积为10,则a2b+ab2的值为_____.
16.矩形![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,
,![]() ,则
,则![]() 的长是__________.
的长是__________.
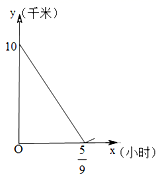
17.甲、乙两家人,相约周末前往中梁国际慢城度周末,甲、乙两家人分别从上桥和童家桥驾车同时出发,匀速前进,且甲途经童家桥,并以相同的线路前往中梁国际慢城. 已知乙的车速为30千米/小时,设两车之间的里程为y(千米),行驶时间为x(小时),图中的折线表示从两家人出发至甲先到达终点的过程中y(千米)与x(小时)的函数关系,根据图中信息,甲的车速为_______千米/小时.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)先化简,再求值:![]() ,其中
,其中![]() 是不等式
是不等式![]() 的正整数解.
的正整数解.
19.(5分)如图,在平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 延长线上的点,且
延长线上的点,且![]() 为等边三角形.
为等边三角形.
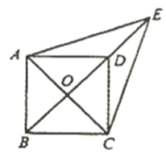
(1)四边形![]() 是菱形吗?请说明理由;
是菱形吗?请说明理由;
(2)若![]() ,试说明:四边形
,试说明:四边形![]() 是正方形.
是正方形.
20.(8分)以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
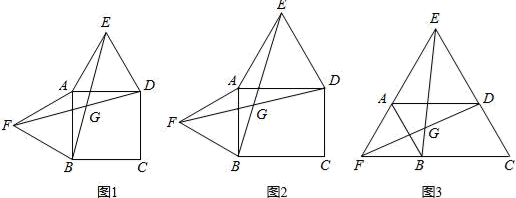
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
21.(10分)某校开展“涌读诗词经典,弘扬传统文化”诗词诵读活动,为了解八年级学生在这次活动中的诗词诵背情况,随机抽取了30名八年级学生,调查“一周诗词诵背数量”,调查结果如下表所示:
一周诗词诵背数量(首) |
|
|
|
|
|
|
人数(人) |
|
|
|
|
|
|
(1)计算这![]() 人平均每人一周诵背诗词多少首;
人平均每人一周诵背诗词多少首;
(2)该校八年级共有6![]() 名学生参加了这次活动,在这次活动中,估计八年级学生中一周诵背诗词
名学生参加了这次活动,在这次活动中,估计八年级学生中一周诵背诗词![]() 首以上(含6首)的学生有多少人.
首以上(含6首)的学生有多少人.
22.(10分)射击队为从甲、乙两名运动员选拔一人参加运动会,对他们进行了六次测试,测试成绩如下表(单位:环)
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)由表格中的数据,计算出甲的平均成绩是 环,乙的成绩是 环.
(2)结合平均水平与发挥稳定性你认为推荐谁参加比赛更适合,请说明理由.
23.(12分)某商品的进价为每件40元,售价每件不低于60元且不高于80元,当售价为每件60元时,每个月可卖出100件;经调查发现,每件商品每上涨1元,每月少卖出2件.设每件商品的售价为x元(x为正整数).
(1)求每个月的销售利润;(用含有x代数式表示)
(2)若每个月的利润为2250元,定价应为多少元?
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、A
2、D
3、D
4、A
5、A
6、B
7、B
8、D
9、B
10、A
11、A
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、1
14、1
15、1.
16、![]()
17、1
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、1.
19、(1)四边形![]() 为菱形,理由见解析;(2)见解析
为菱形,理由见解析;(2)见解析
20、(1)EB=FD,(2)EB=FD,证明见解析;(3)不变,等于60°.
21、(1)5;(2)2640
22、(1)9,9;(2)甲.
23、(1)﹣2x2+300x﹣8800;(2)若每个月的利润为2250元,定价应为65元.
河南省新乡市长垣市2023-2024学年七年级上学期期末数学试题: 这是一份河南省新乡市长垣市2023-2024学年七年级上学期期末数学试题,共15页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
河南省新乡市长垣市2023-2024学年七年级上学期期末数学试题: 这是一份河南省新乡市长垣市2023-2024学年七年级上学期期末数学试题,共14页。
2023-2024学年河南省新乡市长垣市八上数学期末经典模拟试题含答案: 这是一份2023-2024学年河南省新乡市长垣市八上数学期末经典模拟试题含答案,共8页。试卷主要包含了现有7张如图1的长为a,宽为b,下列二次根式中,最简二次根式是,等式0=1成立的条件是等内容,欢迎下载使用。












