


江苏省灌南县2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案
展开江苏省灌南县2022-2023学年七年级数学第二学期期末学业质量监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
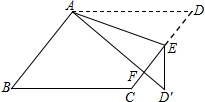
1.如图,在![]() 中,
中,![]() 为边
为边![]() 上一点,将
上一点,将![]() 沿
沿![]() 折叠至
折叠至![]() 处,
处,![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的大小为( )
的大小为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. “学习强国”的英语“Learningpower”中,字母“n”出现的频率是( )
A.1 B.![]() C.
C.![]() D.2
D.2
3.正比例函数y=3x的大致图像是( )
A.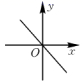 B.
B.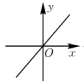 C.
C.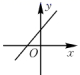 D.
D.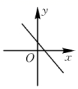
4.点P是图①中三角形上一点,坐标为(a,b),图①经过变化形成图②,则点P在图②中的对应点P’的坐标为( )
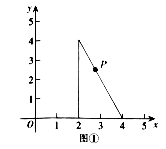
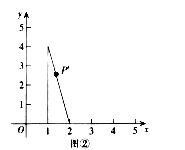
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.不等式组![]() 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.如图,在![]() 中,对角线
中,对角线![]() ,
,![]() 相交于点
相交于点![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,
的中点,![]() 交
交![]() 与点
与点![]() ,则
,则![]() 与
与![]() 的比值是( )
的比值是( )
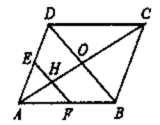
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.如图,已知AB=10,点C,D在线段AB上且AC=DB=2;P是线段CD上的动点,分别以AP,PB为边在线段AB的同侧作等边△AEP和等边△PFB,连接EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是( ).
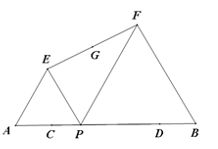
A.6 B.5 C.4 D.3.
8.已知点(-2,y1),(-1,y2),(4,y3)在函数y=![]() 的图象上,则( )
的图象上,则( )
A.y2<y1<y3 B.y1<y2<y3 C.y3<y1<y2 D.y3<y2<y1
9.下列四个图案中,是轴对称图形,但不是中心对称图形的是( )
A.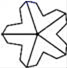 B.
B.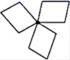 C.
C.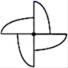 D.
D.
10.关于一次函数y=﹣2x+3,下列结论正确的是( )
A.图象过点(1,﹣1) B.图象经过一、二、三象限
C.y随x的增大而增大 D.当x>![]() 时,y<0
时,y<0
11.对于二次根式![]() ,以下说法不正确的是( )
,以下说法不正确的是( )
A.它是一个无理数 B.它是一个正数 C.它是最简二次根式 D.它有最小值为3
12.若关于![]() 的分式方程
的分式方程![]() 的根是正数,则实数
的根是正数,则实数![]() 的取值范围是().
的取值范围是().
A.![]() ,且
,且![]() B.
B.![]() ,且
,且![]()
C.![]() ,且
,且![]() D.
D.![]() ,且
,且![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.如果关于![]() 的不等式组
的不等式组![]() 无解,则
无解,则![]() 的取值范围是_____.
的取值范围是_____.
14.若![]() 是方程
是方程![]() 的两个实数根,则
的两个实数根,则![]() _______.
_______.
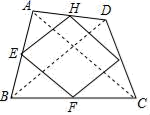
15.如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,连结AC、BD,回答问题
(1)对角线AC、BD满足条件_____时,四边形EFGH是矩形.
(2)对角线AC、BD满足条件_____时,四边形EFGH是菱形.
(3)对角线AC、BD满足条件_____时,四边形EFGH是正方形.
16.在一个不透明的盒子里装有黑、白两种颜色的球共50只,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中.不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1 000 | 3 000 |
摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 620 | 1845 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.620 | 0.615 |
请估计:当n很大时,摸到白球的频率将会接近_____;(精确到0.1)
17.一个不透明的布袋中装有分别标着数字1,2,3,4的四张卡片,现从袋中随机摸出两张卡片,则这两张卡片上的数字之和大于5的概率为_______.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
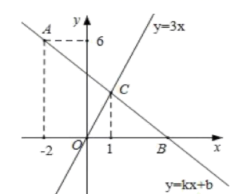
18.(5分)如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求一次函数y=kx+b的解析式;
(2)若点D在y轴负半轴上,且满足S△COD═![]() S△BOC,请直接写出点D的坐标.
S△BOC,请直接写出点D的坐标.
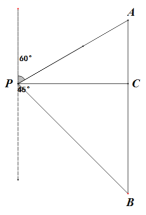
19.(5分)如图,在一次数学课外活动中,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向,办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(结果精确到0.1米).
20.(8分)如图,在平面直角坐标系中,直线![]() 过点
过点![]() 且与
且与![]() 轴交于点
轴交于点![]() ,把点
,把点![]() 向左平移2个单位,再向上平移4个单位,得到点
向左平移2个单位,再向上平移4个单位,得到点![]() .过点
.过点![]() 且与
且与![]() 平行的直线交
平行的直线交![]() 轴于点
轴于点![]() .
.
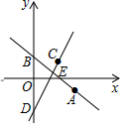
(1)求直线CD的解析式;
(2)直线AB与CD交于点E,将直线CD沿EB方向平移,平移到经过点B的位置结束,求直线CD在平移过程中与x轴交点的横坐标的取值范围.
21.(10分)如图,![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .求证:四边形
.求证:四边形![]() 是菱形.
是菱形.
22.(10分)一次函数图象经过(3,8)和(5,12)两点,求一次函数解析式.
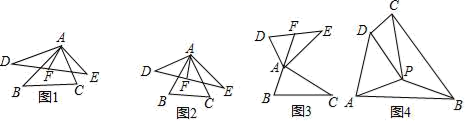
23.(12分)我们定义:如果两个三角形的两组对应边相等,且它们的夹角互补,我们就把其中一个三角形叫做另一个三角形的“夹补三角形”,同时把第三边的中线叫做“夹补中线.例如:图1中,△ABC与△ADE的对应边AB=AD,AC=AE,∠BAC+∠DAE=180°,AF是DE边的中线,则△ADE就是△ABC的“夹补三角形”,AF叫做△ABC的“夹补中线”.
特例感知:
(1)如图2、图3中,△ABC与△ADE是一对“夹补三角形”,AF是△ABC的“夹补中线”;
①当△ABC是一个等边三角形时,AF与BC的数量关系是: ;
②如图3当△ABC是直角三角形时,∠BAC=90°,BC=a时,则AF的长是 ;
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AF与BC的关系,并给予证明.
拓展应用:
(3)如图4,在四边形ABCD中,∠DCB=90°,∠ADC=150°,BC=2AD=6,CD=![]() ,若△PAD是等边三角形,求证:△PCD是△PBA的“夹补三角形”,并求出它们的“夹补中线”的长.
,若△PAD是等边三角形,求证:△PCD是△PBA的“夹补三角形”,并求出它们的“夹补中线”的长.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
2、C
3、B
4、A
5、B
6、C
7、D
8、A
9、A
10、D
11、A
12、D
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、a≤1.
14、10
15、AC⊥BD AC=BD AC⊥BD且AC=BD
16、0.60
17、![]()
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)y=−x+4;(2)(0,−6)
19、教学楼A与办公楼B之间的距离大约为94.6米.
20、(1)y=3x-10;(2)![]()
21、详见解析
22、y=1x+1.
23、(1)AF=![]() BC;
BC;![]() a;(2)猜想:AF=
a;(2)猜想:AF=![]() BC,(3)
BC,(3)![]()
江苏省连云港市灌南县2022-2023学年七年级数学第二学期期末质量检测模拟试题含答案: 这是一份江苏省连云港市灌南县2022-2023学年七年级数学第二学期期末质量检测模拟试题含答案,共6页。试卷主要包含了一元二次方程的根的情况为,如图,已知A,分式的计算结果是等内容,欢迎下载使用。
江苏省盐城初级中学2022-2023学年数学七年级第二学期期末学业质量监测模拟试题含答案: 这是一份江苏省盐城初级中学2022-2023学年数学七年级第二学期期末学业质量监测模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,已知,一组数据,在直角坐标系中,点P,下列各等式成立的是等内容,欢迎下载使用。
江苏省南京鼓楼区2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案: 这是一份江苏省南京鼓楼区2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案,共7页。












