江苏省无锡市和桥区2022-2023学年七年级数学第二学期期末学业质量监测试题含答案

江苏省无锡市和桥区2022-2023学年七年级数学第二学期期末学业质量监测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考试结束后，请将本试卷和答题卡一并交回．

2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．

4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．

5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．

一、选择题(每小题3分,共30分)

1．计算的结果是（　　）

A．4 B．± C．2 D．

2．下列说法不正确的是（  ）

A．有两组对边分别平行的四边形是平行四边形

B．平行四边形的对角线互相平分

C．平行四边形的对边平行且相等

D．平行四边形的对角互补，邻角相等

3．下列成语所描述的事件为随机事件的是（　　）

A．守株待兔 B．水中捞月 C．瓮中捉鳖 D．拔苗助长

4．下列命题中，是真命题的是（  ）

A．对角线互相垂直的四边形是菱形 B．对角形相等的四边形是矩形

C．顺次连结平行四边形各边中点所得四边形是平行四边形 D．一组邻边相等的平行四边形是正方形

5．若等腰三角形的周长为18cm，其中一边长为4cm，则该等腰三角形的底边长为（　　）

A．10 B．7或10 C．4 D．7或4

6．已知是方程的一个根，那么代数式的值为（    ）

A．5 B．6 C．7 D．8

7．下列命题：①任何数的平方根有两个；②如果一个数有立方根，那么它一定有平方根；③算术平方根一定是正数；④非负数的立方根不一定是非负数.错误的个数为（      ）

A．1    B．2    C．3    D．4

8．如果等腰三角形两边长是6和3，那么它的周长是(     ）

A．15或12 B．9 C．12 D．15

9．甲、乙两台机床同时生产一种零件，在5天中，两台机床每天出次品的数量如下表：

关于以上数据的平均数、中位数、众数和方差，说法不正确的是(   )

A．甲、乙的平均数相等 B．甲、乙的众数相等

C．甲、乙的中位数相等 D．甲的方差大于乙的方差

10．在垃圾分类打卡活动中，小丽统计了本班月份打卡情况：次的有人，次的有人，次的有人，次的有人，则这个班同学垃圾分类打卡次数的中位数是（    ）

A．次 B．次 C．次 D．次

二、填空题(本大题共有6小题，每小题3分，共18分)

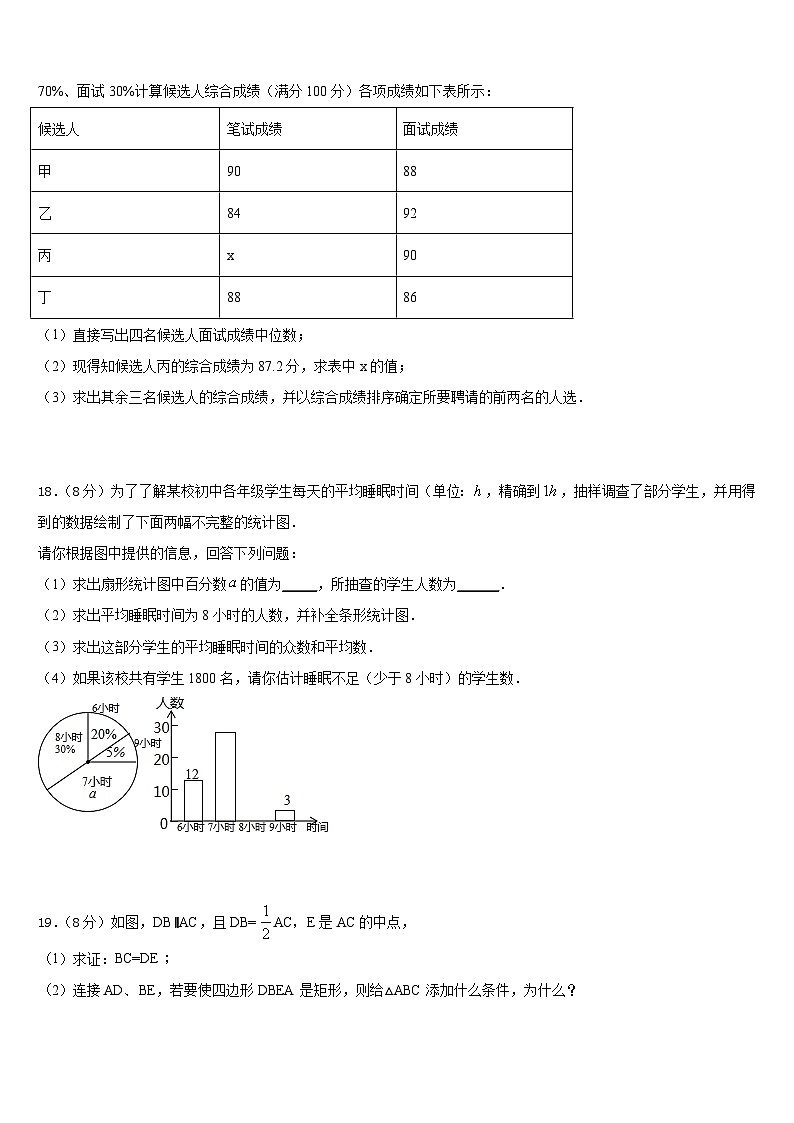
11．函数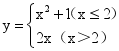,则当函数值y=8时,自变量x的值是_____.

12．如图所示，平行四边形中，点在边上，以为折痕，将向上翻折，点正好落在上的处，若的周长为8，的周长为22，则的长为__________．

13．已知，则的值为__________．

14．点 P（1，﹣3）关于原点对称的点的坐标是_____．

15．使有意义的x的取值范围是______．

16．如图，平行四边形 的周长为 , 相交于点 ， 交 于点 ，则 的周长为________ .

三、解下列各题(本大题共8小题，共72分)

17．（8分）某公司招聘职员两名，对甲乙丙丁四名候选人进行笔试和面试，各项成绩均为100分，然后再按笔试70%、面试30%计算候选人综合成绩（满分100分）各项成绩如下表所示：

（1）直接写出四名候选人面试成绩中位数；

（2）现得知候选人丙的综合成绩为87.2分，求表中x的值；

（3）求出其余三名候选人的综合成绩，并以综合成绩排序确定所要聘请的前两名的人选．

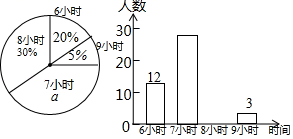
18．（8分）为了了解某校初中各年级学生每天的平均睡眠时间（单位：，精确到，抽样调查了部分学生，并用得到的数据绘制了下面两幅不完整的统计图．

请你根据图中提供的信息，回答下列问题：

（1）求出扇形统计图中百分数的值为_____，所抽查的学生人数为______．

（2）求出平均睡眠时间为8小时的人数，并补全条形统计图．

（3）求出这部分学生的平均睡眠时间的众数和平均数．

（4）如果该校共有学生1800名，请你估计睡眠不足（少于8小时）的学生数．

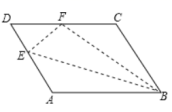
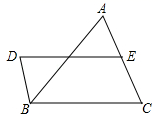
19．（8分）如图，DB∥AC，且DB=AC，E是AC的中点，

（1）求证：BC=DE；

（2）连接AD、BE，若要使四边形DBEA是矩形，则给△ABC添加什么条件，为什么？

20．（8分）（阅读材料）

解方程：.

解：设，则原方程变为.

解得，，.

当时，，解得.

当时，，解得.

所以，原方程的解为，，，.

（问题解决）

利用上述方法，解方程：.

21．（8分）如图，在矩形中，为边上一点，连接，过点作，垂足为，若，.

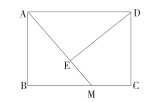
(1)求证：；

(2)求的长(结果用根式表示).

22．（10分）解答下列各题：

（1）计算：；

（2）当时，求代数式的值.

23．（10分）已知y与x-1成正比例，且当x=3时，y=4.

（1）写出y与x之间的函数表达式；

（2）当x= -2时，求y的值；

（3）当y=0时，求x的值

24．（12分）如图①，四边形是正方形，点是边的中点， ，且交正方形的外角平分线于点请你认真阅读下面关于这个图形的探究片段，完成所提出的问题.

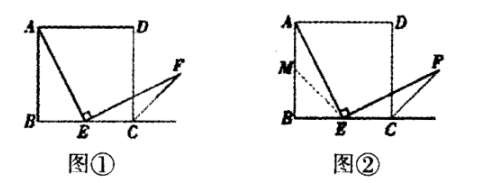
（1）探究1：小强看到图①后，很快发现这需要证明AE和EF所在的两个三角形全等，但△ABE和△ECF显然不全等（个直角三角形，一个钝角三角形）考虑到点E是边BC的中点，因此可以选取AB的中点M（如图②），连接EM后尝试着去证明就行了.随即小强写出了如下的证明过程：

证明：如图②，取AB的中点M，连接EM.

∵

∴

又∵

∴

∵点E、M分别为正方形的边BC和AB的中点，

∴

∴是等腰直角三角形，

∴

又∵是正方形外角的平分线，

∴，∴

∴

∴，

∴

（2）探究2：小强继续探索，如图③，若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”，其余条件不变，发现AE=EF仍然成立小强进一步还想试试，如图④，若把条件“点E是边BC的中点”为“点E是边BC延长线上的一点”，其余条件仍不变，那么结论AE=EF仍然成立请你选择图③或图④中的一种情况写出证明过程给小强看.

参考答案

一、选择题(每小题3分,共30分)

1、C

2、D

3、A

4、C

5、C

6、C

7、D

8、D

9、B

10、C

二、填空题(本大题共有6小题，每小题3分，共18分)

11、或4

12、1.

13、

14、（-1，3）

15、

16、1

三、解下列各题(本大题共8小题，共72分)

17、（1）89分；（2）86；（3）甲的综合成绩： 89.4分，乙的综合成绩： 86.4分，丁的综合成绩为87.4分，以综合成绩排序确定所要招聘的前两名的人选是：甲、丁．

18、（1）45%，60人；（2）18人，条形统计图见解析；（3）众数7，平均数7.2；（4）1170人．

19、（1）证明见解析（2）添加AB=BC

20、，，，

21、（1）见解析；（2）.

22、（1）（2）1.

23、 (1) ;(2)-6;(3)1

24、见解析