


2022-2023学年江苏省无锡市和桥区、张渚区七下数学期末考试模拟试题含答案
展开2022-2023学年江苏省无锡市和桥区、张渚区七下数学期末考试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知![]() 、
、![]() 是一次函数
是一次函数![]() 图象上的两个点,则
图象上的两个点,则![]() 与
与![]() 的大小关系为( )
的大小关系为( )
A.![]() B.
B.![]() C.
C.![]() D.不能确定
D.不能确定![]() 与
与![]() 的大小
的大小
2.如图所示的是一扇高为2m,宽为1.5m的长方形门框,光头强有一些薄木板要通过门框搬进屋内,在不能破坏门框,也不能锯短木板的情况下,能通过门框的木板最大的宽度为( )
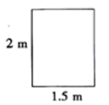
A.1.5m B.2m C.2.5m D.3m
3.下列图形中,不是轴对称图形的是( )
A.矩形 B.菱形 C.平行四边形 D.正方形
4.自2011年以来长春市己连续三届被评为“全国文明城市”,为了美化城市环境,今年长春市计划种植树木30万棵,由于志愿者的加入,实际每天植树比原计划多20%,结果提前5天完成任务,设原计划每天植树![]() 万棵,可列方程是( )
万棵,可列方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.若直线y=-2x-4与直线y=4x+b的交点在第三象限,则b的取值范围是( )
A.-4<b<8 B.-4<b<0 C.b<-4或b>8 D.-4≤6≤8
6.若关于x的不等式组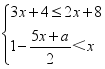 有且仅有5个整数解,且关于y的分式方程
有且仅有5个整数解,且关于y的分式方程![]() 有非负整数解,则满足条件的所有整数a的和为( )
有非负整数解,则满足条件的所有整数a的和为( )
A.12 B.14 C.21 D.33
7.下列运算结果正确的是( )
A.![]() =﹣3 B.(﹣
=﹣3 B.(﹣![]() )2=2 C.
)2=2 C.![]() ÷
÷![]() =2 D.
=2 D.![]() =±4
=±4
8.已知正比例函数![]() 的函数值
的函数值![]() 随
随![]() 的增大而减小,则一次函数
的增大而减小,则一次函数![]() 的图象大致是( )
的图象大致是( )
A.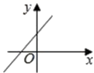 B.
B.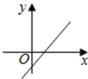 C.
C.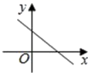 D.
D.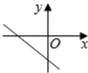
9.在![]() 中,
中,![]() ,则
,则![]() 的值是( )
的值是( )
A.12 B.8 C.6 D.3
10.如图,把一个矩形纸片ABCD沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′为( )。
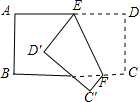
A.70° B.65° C.50° D.25°
11.一同学将方程![]() 化成了
化成了![]() 的形式,则m、n的值应为( )
的形式,则m、n的值应为( )
A.m=1.n=7 B.m=﹣1,n=7 C.m=﹣1,n=1 D.m=1,n=﹣7
12.如图,![]() 为等边三角形,
为等边三角形,![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 于点
于点![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
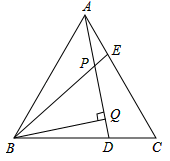
A.7 B.8 C.9 D.10
二、填空题(每题4分,满分20分,将答案填在答题纸上)
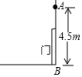
13.如图,有一个由传感器A控制的灯,要装在门上方离地面4.5m的墙上,任何东西只要移至该灯5m及5m内,灯就会自动发光,小明身高1.5m,他走到离墙_______的地方灯刚好发光.
14.计算: ![]() =______________
=______________
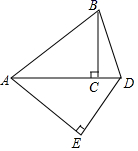
15.如图,在△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕点A顺时针旋转得到△ADE(其中点B恰好落在AC延长线上点D处,点C落在点E处),连接BD,则四边形AEDB的面积为______.
16.化简![]() 的结果为___________
的结果为___________
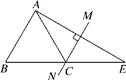
17.如图,在△ABE中,∠E=30°,AE的垂直平分线MN交BE于点C,且AB=AC,则∠B=________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)如图,已知![]() 、
、![]() 分别是平行四边形
分别是平行四边形![]() 的边
的边![]() 、
、![]() 上的点,且
上的点,且![]() .
.
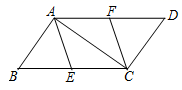
求证:四边形![]() 是平行四边形.
是平行四边形.
19.(5分)因式分解:![]()
20.(8分)如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE,
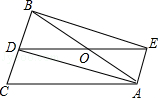
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
21.(10分)为积极响应新旧功能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为35万元时,年销售量为550台;每台售价为40万元时,年销售量为500台.假定该设备的年销售量![]() (单位:台)和销售单价
(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于60万元,如果该公司想获得8000万元的年利润,则该设备的销售单价应是多少万元?
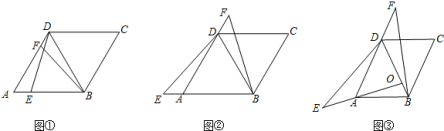
22.(10分)感知:如图![]() ,在菱形ABCD中,
,在菱形ABCD中,![]() ,点E、F分别在边AB、AD上
,点E、F分别在边AB、AD上![]() 若
若![]() ,易知
,易知![]() ≌
≌![]() .
.
探究:如图![]() ,在菱形ABCD中,
,在菱形ABCD中,![]() ,点E、F分别在BA、AD的延长线上
,点E、F分别在BA、AD的延长线上![]() 若
若![]() ,
,![]() 与
与![]() 是否全等?如果全等,请证明;如果不全等,请说明理由.
是否全等?如果全等,请证明;如果不全等,请说明理由.
拓展:如图![]() ,在▱ABCD中,
,在▱ABCD中,![]() ,点O是AD边的垂直平分线与BD的交点,点E、F分别在OA、AD的延长线上
,点O是AD边的垂直平分线与BD的交点,点E、F分别在OA、AD的延长线上![]() 若
若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
23.(12分)先化简:(![]() ﹣1)÷
﹣1)÷![]() ,再0,1,2,﹣1中选择一个恰当的x值代入求值.
,再0,1,2,﹣1中选择一个恰当的x值代入求值.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、C
2、C
3、C
4、A
5、A
6、B
7、B
8、B
9、C
10、C
11、B
12、C
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、4米
14、2![]()
15、![]()
16、![]()
17、60°
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、见解析.
19、(x+y-1)(x+y+1)
20、解:(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形.
∵AB=AC,AD是△ABC的角平分线,∴AD⊥BC.
∴∠ADB=90°.
∴平行四边形AEBD是矩形.
(2)当∠BAC=90°时,矩形AEBD是正方形.理由如下:
∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,∴AD=BD=CD.
∵由(1)得四边形AEBD是矩形,∴矩形AEBD是正方形.
21、(1)年销售量![]() 与销售单价
与销售单价![]() 的函数关系式为
的函数关系式为![]() ;(2)该设备的销售单价应是50万元/台.
;(2)该设备的销售单价应是50万元/台.
22、探究:![]() 和
和![]() 全等,理由见解析;拓展:
全等,理由见解析;拓展:![]() .
.
23、-1
2023-2024学年江苏省无锡市和桥区、张渚区九上数学期末达标测试试题含答案: 这是一份2023-2024学年江苏省无锡市和桥区、张渚区九上数学期末达标测试试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
江苏省无锡市和桥区、张渚区2023-2024学年八上数学期末检测模拟试题含答案: 这是一份江苏省无锡市和桥区、张渚区2023-2024学年八上数学期末检测模拟试题含答案,共6页。试卷主要包含了下列六个数,计算 的结果是,下列各式中正确的是,直线,如果,那么代数式的值是.等内容,欢迎下载使用。
江苏省无锡市和桥区2023-2024学年八上数学期末监测模拟试题含答案: 这是一份江苏省无锡市和桥区2023-2024学年八上数学期末监测模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,如图所示,如图,火车匀速通过隧道,下列约分正确的是,如果将分式等内容,欢迎下载使用。












