


江苏省宜兴市桃溪中学2022-2023学年七年级数学第二学期期末达标检测试题含答案
展开江苏省宜兴市桃溪中学2022-2023学年七年级数学第二学期期末达标检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
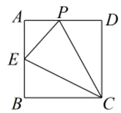
1.如图,正方形![]() 的边长为4,点
的边长为4,点![]() 是
是![]() 的中点,点
的中点,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 移动至终点
移动至终点![]() ,设
,设![]() 点经过的路径长为
点经过的路径长为![]() ,
,![]() 的面积为
的面积为![]() ,则下列图象能大致反映
,则下列图象能大致反映![]() 与
与![]() 函数关系的是( )
函数关系的是( )
A.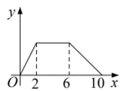 B.
B.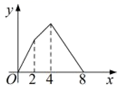 C.
C.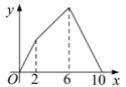 D.
D.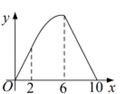
2.将不等式![]() <2的解集表示在数轴上,正确的是( )
<2的解集表示在数轴上,正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.为了解2019年泰兴市八年级学生的视力情况,从中随机调查了500名学生的视力情况.下列说法正确的是( )
A.2016年泰兴市八年级学生是总体 B.每一名八年级学生是个体
C.500名八年级学生是总体的一个样本 D.样本容量是500
4.下列长度的三条线段能组成三角形的是( )
A.1,2,3 B.2,2,4 C.3,4,5 D.3,4,8
5.如图,在▱ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长等于( )
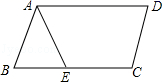
A.8cm B.6cm C.4cm D.2cm
6.已知四边形ABCD是平行四边形,下列结果正确的是( )
A.当AB=BC时,它是矩形 B.![]() 时,它是菱形
时,它是菱形
C.当∠ABC=90°时,它是菱形 D.当AC=BD时,它是正方形
7.一个直角三角形两条直角边的长分别为5,12,则其斜边上的高为( )
A.![]() B.13 C.6 D.25
B.13 C.6 D.25
8.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
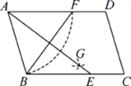
A.4 B.8 C.6 D.10
9.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 边的中点,
边的中点,![]() 于
于![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
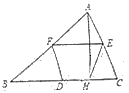
A.32 B.16 C.8 D.10
10.质量检查员随机抽取甲、乙、丙、丁四台机器生产的20个乒乓球的直径(规格是直径4cm),整理后的平均数和方差如下表,那么这四台机器生产的乒乓球既标准又稳定的是( )
机器 | 甲 | 乙 | 丙 | 丁 |
平均数(单位:cm) | 4.01 | 3.98 | 3.99 | 4.02 |
方差 | 0.03 | 2.4 | 1.1 | 0.3 |
A.甲 B.乙 C.丙 D.丁
二、填空题(本大题共有6小题,每小题3分,共18分)
11.如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于![]() 的二元一次方程组的解是______ .
的二元一次方程组的解是______ .
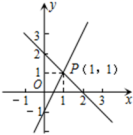
12.某水库的水位在5小时内持续上涨,初始的水位高度为6米,水位以每小时0.3米的速度匀速上升,则水库的水位高度y米与时间x小时(0≦x≦5)的函数关系式为___
13.如图,在□ABCD中,AB=5,AD=6,将□ABCD沿AE翻折后,点B恰好与点 C重合,则折痕AE的长为____.
14.当m=_____时,![]() 是一次函数.
是一次函数.
15.在函数![]() 的图象上有两个点
的图象上有两个点![]() ,
,![]() ,则
,则![]() 的大小关系是___________.
的大小关系是___________.
16.已知二次函数y=-x![]() -2x+3的图象上有两点A(-7,
-2x+3的图象上有两点A(-7,![]() ),B(-8,
),B(-8,![]() ),则
),则![]() ▲
▲ ![]() .(用>、<、=填空).
.(用>、<、=填空).
三、解下列各题(本大题共8小题,共72分)
17.(8分)已知![]() ,求
,求![]() 的值.
的值.
18.(8分)点![]() 向__________平移2个单位后,所对应的点的坐标是
向__________平移2个单位后,所对应的点的坐标是![]() .
.
19.(8分)(1)分解因式:①![]() ②
②![]()
(2)解不等式组,并把解集在数轴上表示出来. 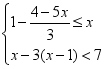
20.(8分)中国新版高铁“复兴号”率先在北京南站和上海虹桥站双向首发“复兴号”高铁从某车站出发,在行驶过程中速度![]() (千米/分钟)与时间
(千米/分钟)与时间![]() (分钟)的函数关系如图所示.
(分钟)的函数关系如图所示.
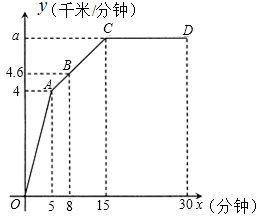
(1)当![]() 时,求
时,求![]() 关于
关于![]() 工的函数表达式,
工的函数表达式,
(2)求点![]() 的坐标.
的坐标.
(3)求高铁在![]() 时间段行驶的路程.
时间段行驶的路程.
21.(8分)为了迎接“六一”国际儿童节,某童装品牌专卖店准备购进甲、乙两种童装,这两种童装的进价和售价如下表:
价格 | 甲 | 乙 |
进价(元/件) | m | m+20 |
售价(元/件) | 150 | 160 |
如果用5000元购进甲种童装的数量与用6000元购进乙种童装的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种童装共200件的总利润(利润=售价﹣进价)不少于8980元,且甲种童装少于100件,问该专卖店有哪几种进货方案?
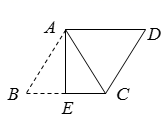
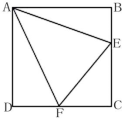
22.(10分)如图,E与F分别在正方形ABCD边BC与CD上,∠EAF=45°.
(1)以A为旋转中心,将△ABE按顺时针方向旋转90°,画出旋转后得到的图形.
(2)已知BE=2cm,DF=3cm,求EF的长.
23.(10分)已知a=![]() ,b=
,b=![]() ,
,
(1)求ab,a+b的值;
(2)求![]() 的值.
的值.
24.(12分)如图,在平行四边形ABCD中,E为BC边上一点,连结AE、BD且AE=AB
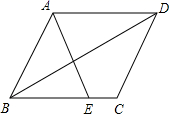
(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、D
3、D
4、C
5、C
6、B
7、A
8、B
9、B
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、y=6+0.3x
13、1
14、3或0
15、y1>y2
16、>。
三、解下列各题(本大题共8小题,共72分)
17、![]()
18、左
19、 (1)① ![]() ;②
;②![]() ;(2)
;(2)![]()
20、(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)高铁在
;(3)高铁在![]() 时段共行驶了
时段共行驶了![]() 千米.
千米.
21、(1)m=100(2)两种方案
22、(1)见解析;(2)5cm.
23、(1)ab=1,a+b=2![]() ;(2)1.
;(2)1.
24、(1)证明见解析;(2)证明见解析.
2023-2024学年江苏省宜兴市桃溪中学数学九年级第一学期期末监测试题含答案: 这是一份2023-2024学年江苏省宜兴市桃溪中学数学九年级第一学期期末监测试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号等内容,欢迎下载使用。
江苏省宜兴市桃溪中学2023-2024学年数学八年级第一学期期末学业质量监测试题含答案: 这是一份江苏省宜兴市桃溪中学2023-2024学年数学八年级第一学期期末学业质量监测试题含答案,共7页。试卷主要包含了答题时请按要求用笔,尺规作图要求,如图,已知等内容,欢迎下载使用。
2023-2024学年江苏省无锡市宜兴市桃溪中学数学八年级第一学期期末统考试题含答案: 这是一份2023-2024学年江苏省无锡市宜兴市桃溪中学数学八年级第一学期期末统考试题含答案,共7页。试卷主要包含了已知,平面直角坐标系中,点P等内容,欢迎下载使用。












