2022-2023学年江苏省宜兴市陶都中学数学七年级第二学期期末检测试题含答案

2022-2023学年江苏省宜兴市陶都中学数学七年级第二学期期末检测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题(每小题3分,共30分)

1．一元二次方程的解是（  ）

A． B．

C． D．

2．某同学一周中每天完成家庭作业所花时间（单位：分钟）分别为：35，40，45，40，55，40，1．这组数据的众数是( )

A．35 B．40 C．45 D．55

3．如图，被笑脸盖住的点的坐标可能是（　　）

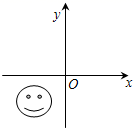
A．（3，2） B．（-3，2） C．（-3，-2） D．（3，-2）

4．在菱形中，对角线相交于点，，则的长为（  ）

A． B． C． D．

5．平面直角坐标系中，点A的坐标为，将线段OA绕原点O逆时针旋转得到，则点的坐标是　　

A． B． C． D．

6．如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=15，则S2的值是(     )

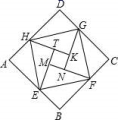
A．3 B． C．5 D．

7．下列各式因式分解正确的是（   ）

A． B．

C． D．

8．如图，要测量被池塘隔开的A、C两点间的距离，李师傅在AC外任选一点B，连接BA和BC，分别取BA和BC的中点E、F，量得EF两点间距离等于23米，则A、C两点间的距离为（）米

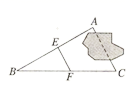
A．23 B．46 C．50 D．2

9．一次函数y=kx+1，y随x的增大而减小，则一次函数的图象不经过（　　）

A．第一象限    B．第二象限    C．第三象限    D．第四象限

10．要使分式有意义，则x应满足的条件是（　　）

A．x≠1 B．x≠1或x≠0 C．x≠0 D．x＞1

二、填空题(本大题共有6小题，每小题3分，共18分)

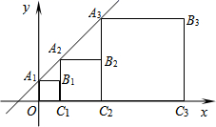
11．如图，正方形A1B1C1O,A2B2C2C1，A3B3C3C2, ……，按如图的方式放置．点A1,A2，A3，……和点C1,C2，C3……分别在直线y＝x +1和x轴上，则点A6的坐标是____________．

12．有8个数的平均数是11，还有12个数的平均数是12，则这20个数的平均数是_________．

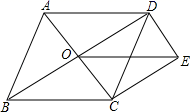
13．如图，在菱形ABCD中，AC、BD交于点O，AC＝6，BD＝8，若DE∥AC，CE∥BD，则OE的长为_____．

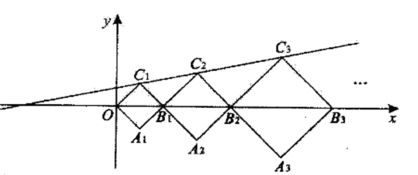
14．如图，在平面直角坐标系中，正方形OA1B1C1，B1A2B2C2，B2A3B3C3，···的顶点B1，B2，B3，···在x轴上，顶点C1，C2，C3···在直线y=kx+b上，若正方形OA1B1C1，B1A2B2C2的对角线OB1=2，B1B2=3, 则点C5的纵坐标是_____．

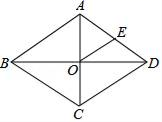
15．如图，在菱形ABCD中，AC、BD交于点O，AC＝4，菱形ABCD的面积为4，E为AD的中点，则OE的长为___．

16．为了改善生态环境，防止水土流失，红旗村计划在荒坡上种树960棵，由于青年志愿者支援，实际每天种树的棵数是原计划的2倍，结果提前4天完成任务，则原计划每天种树的棵数是________.

三、解下列各题(本大题共8小题，共72分)

17．（8分）如图，在△ABC中，∠ACB=90°，AC=8，BC=1．CD⊥AB于点D．点P从点A出发，以每秒1个单位长度的速度沿线段AB向终点B运动．在运动过程中，以点P为顶点作长为2，宽为1的矩形PQMN，其中PQ=2，PN=1，点Q在点P的左侧，MN在PQ的下分，且PQ总保持与AC垂直．设P的运动时间为t（秒）（t＞0），矩形PQMN与△ACD的重叠部分图形面积为S（平方单位）．

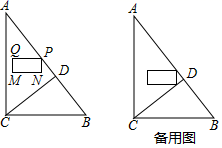
（1）求线段CD的长；

（2）当矩形PQMN与线段CD有公共点时，求t的取值范围；

（3）当点P在线段AD上运动时，求S与t的函数关系式．

18．（8分）已知，矩形ABCD中，AB＝4cm，BC＝8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．

（1）如图（1），连接AF、CE．

①四边形AFCE是什么特殊四边形？说明理由；      

②求AF的长；

（2）如图（2），动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．

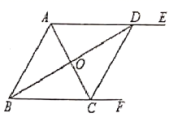
19．（8分）如图，，平分，交于点，平分，交于点，连接.求证：四边形是菱形.

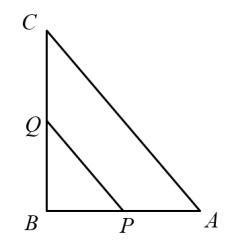
20．（8分）如图，在中，，，，点从点开始沿边向点以的速度移动，点从点开始沿边向点以2的速度移动．

（1）如果点，分别从点，同时出发，那么几秒后，的面积等于6？

（2）如果点，分别从点，同时出发，那么几秒后，的长度等于7？

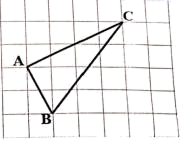
21．（8分）如图，在正方形网格中，每个小正方形的边长为 1，ABC 为格点三角形（即 A, B, C 均 为格点），求 BC 上的高.

22．（10分）解不等式组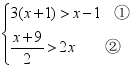，并将解集在数轴上表示出来．

23．（10分）每年的6月5日为世界环保日，为了提倡低碳环保，某公司决定购买10台节省能源的新设备，现有A、B两种型号的设备可供选购，A、B两种型号的设备每台的价格分别为12万元和10万元

(1)该公司经预算决定购买节省能源的新设备的资金不超过110万元，则A型设备最多购买多少台？

(2)已知A型设备的产量为240吨/月，B型设备的产量为180吨/月，若每月要求总产量不低于2040吨，则A型设备至少要购买多少台？

24．（12分）甲、乙两校参加区教育局举办的学生英语口语竞赛，两校参赛人数相等.比赛结束后，发现学生成绩分别为7分、8分、9分、10分（满分为10分）.依据统计数据绘制了如图所示的尚不完整的统计图表.

甲校成绩统计表

（1）在图①中，“7分”所在扇形的圆心角等于______；

（2）请你将②的统计图补充完整；

（3）经计算，乙校的平均分是8.3分，中位数是8分，请写出甲校的平均分、中位数；并从平均分和中位数的角度分析哪个学校成绩较好；

（4）如果该教育局要组织8人的代表队参加市级团体赛，为便于管理，决定从这两所学校中的一所挑选参赛选手，请你分析，应选哪所学校？

参考答案

一、选择题(每小题3分,共30分)

1、D

2、B

3、C

4、D

5、A

6、C

7、A

8、B

9、C

10、A

二、填空题(本大题共有6小题，每小题3分，共18分)

11、（31，32）

12、11.1

13、1

14、（，）

15、

16、120

三、解下列各题(本大题共8小题，共72分)

17、（1）CD＝；（2）≤t≤；（3）当0＜t＜时，S＝；当≤t≤时， S＝2；当＜t≤时，S＝．

18、（1） ①菱形，理由见解析；②AF＝1；（2） 秒．

19、详见解析

20、（1）出发1秒后，的面积等于6；（2）出发0秒或秒后，的长度等于7．

21、.

22、，数轴表示见解析

23、 (1)A型设备最多购买5台；(2)A型设备至少要购买4台．

24、（1）144°；（2）乙校得8分的学生的人数为3人，据此可将图②的统计图补充完整如图③见解析；（3）从平均分和中位数的角度分析乙校成绩较好；（4）应选甲校.