沪科版七年级下册6.2 实数获奖第1课时教学设计

6.2 实数

第1课时 实数的概念及分类

【知识与技能】

1.了解无理数和实数的概念.

2.会对实数进行分类.

3.会用“夹逼法”估计一个无理数的大小，会将循环小数化为分数.

【过程与方法】

从实际问题引出无理数，会用“夹逼法”估计无理数的大小，能用两种方法对实数进行分类，增强学生的参与意识，发挥学生的积极主动性.

【情感态度】

让学生在独立思考的基础上，积极参与数学问题的讨论，勇于发表自己的观点，增强合作交流意识，激发学生的学习兴趣.

【教学重点】

掌握无理数的三种形式，能够识别有理数和无理数，能对实数进行分类.

【教学难点】

循环小数化为分数的规律与方法.

一、情境导入，初步认识

问题如图是由4条横线，5条竖线构成的方格网，它们相邻的行距，列距都是1，从这些纵横线相交得出的20个点（称为格点）中，我们可以选择其中4个格点作为顶点连接成一个正方形，叫做格点正方形.你能找出多少种面积互不相同的格点正方形？

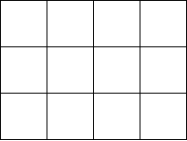
（1）有面积分别是1，4，9的格点是正方形吗？

（2）有面积是2的格点正方形吗？把它画出来.

（3）还有与这些面积不相同的格点正方形吗？

【教学说明】教师提出问题，学生自主探究然后相互交流，第（1）问学生很容易得到答案，第（2）问教师可适当加入引导启发.

二、思考探究，获取新知

1.问：我们看到四个边长为1的相邻正方形的对角线就围成一个面积为2的格点正方形这种正方形的边长应是多少？

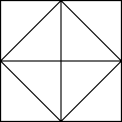
【教学说明】学生自然联想到平方根这一节所学知识，很容易得出这种正方形的边长为 .

探究 是一个怎样的数呢？

因为12=1<2,22=4>2.

所以1<<2，这说明2不可能是整数.

因为1.42=1.96<2,1.52=2.25>2.

所以1.4<<1.5.

类似地，可得1.414<<1.415.

像上面这样一直做下法，可以得到：

=1.41412135…这说明是一个无限不循环小数.

【归纳结论】无限不循环小数叫做无理数.

任何整数、分数都可以化为有限小数或无限循环小数，反过来，任何有限小数和无限循环小数都可以写成分数形式，因此有理数是有限小数或无限循环小数；而无理数是无限不循环小数.

2.实数的分类.

问：有理数和无理数统称为实数，这样，我们认识的数的范围又一次扩大了，我们该怎样对实数进行分类呢？

【教学说明】教师提出问题，学生思考尝试，然后相互交流，掌握实数的两种分类方法.

【归纳结论】我们可以将实数按如下方式分类：

有理数、无理数都有正、负之分，实数也可以作如下分类：

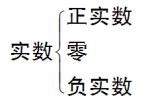
三、典例精析，掌握新知

【教学说明】教师给出例题后，让学生独立完成，然后让部分学生上台展示自己的答案，加深对所学新知识的理解.

四、运用新知，深化理解

1.把下列各数分类填入图中:

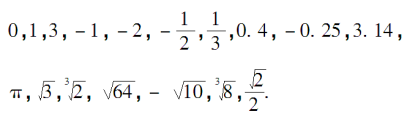
2.把下列各数写成分数形式：

3.判断是非：

（1）无限小数都是无理数.(        )

(2)无限不循环小数是无理数.(        )

(3)无理数是带根号的数.(        )

(4)分数是无理数.(        )

4.下列各组数都是无理数的是（      ）

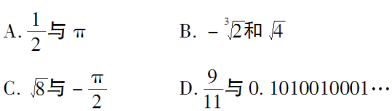
【教学说明】教师展示习题，学生独立完成，教师巡视，对学生的疑惑及时给予指导.

五、师生互动，课堂小结

通过这节课的学习，你掌握了哪些新知识？还有哪些疑问？请与同伴交流.

【教学说明】学生相互交流，回顾无理数、实数的概念以及实数的分类，加深对所学知识的理解.

完成练习册中本课时练习.

从实际问题中引出无理数，进而引出实数并对实数进行分类，学生积极主动探索，教师引导启发，学生合作交流，培养学生继续探索的兴趣.