中考数学专题突破━相似模型的应用课件

这是一份中考数学专题突破━相似模型的应用课件，共33页。PPT课件主要包含了生活数学，变式练习1，知二求一，六中知二求四，变式练习2，变式练习3，变式练习4，常用相似模型，生活数学享受之美，体验中考展示自我等内容，欢迎下载使用。

2023年中考数学专题突破 ━━ 相似模型的应用课件（33张ppt）
在创文创卫活动中，恩施市积极响应，对城区一圆形水上乐园改造升级，在其圆周上安装音乐喷泉，提升旅游服务质量.其平面结构如右图，A、B、C、D在 ⊙O 上，AB为直径，AB CD，只有BC、BE可通过地面的装饰材料尺寸估算出BC=30米，BE=18米，只借助估算两数据你能求出圆的周长吗？若能，求其周长.
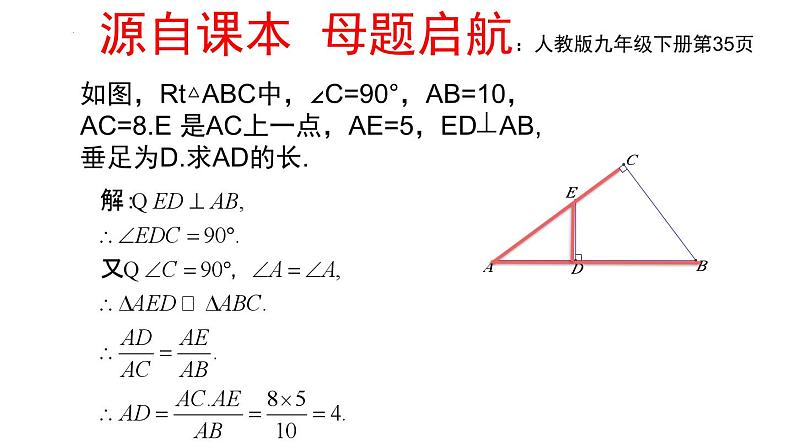
如图，Rt△ABC中，∠C=90°，AB=10，AC=8.E 是AC上一点，AE=5，ED AB,垂足为D.求AD的长.
源自课本 母题启航：人教版九年级下册第35页
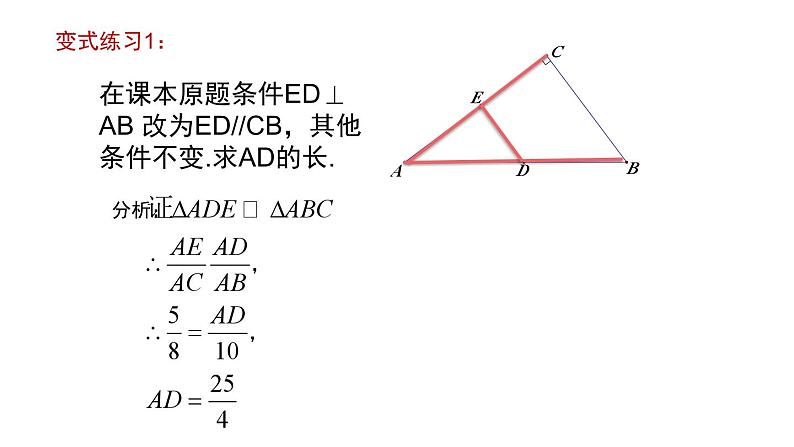
在课本原题条件ED AB 改为ED//CB，其他条件不变.求AD的长.
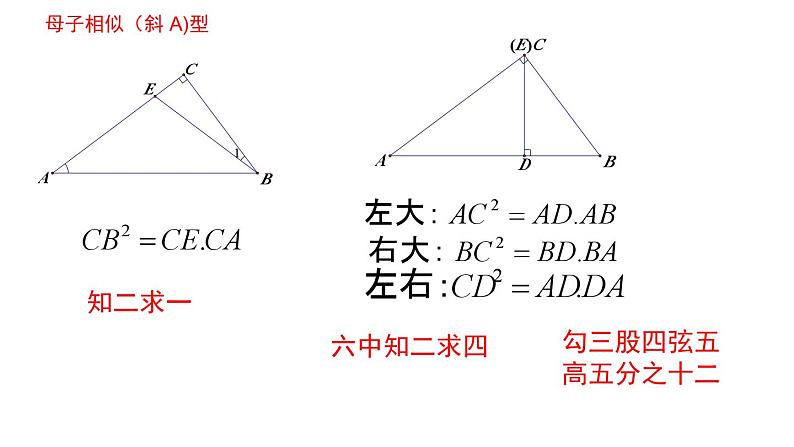
勾三股四弦五高五分之十二
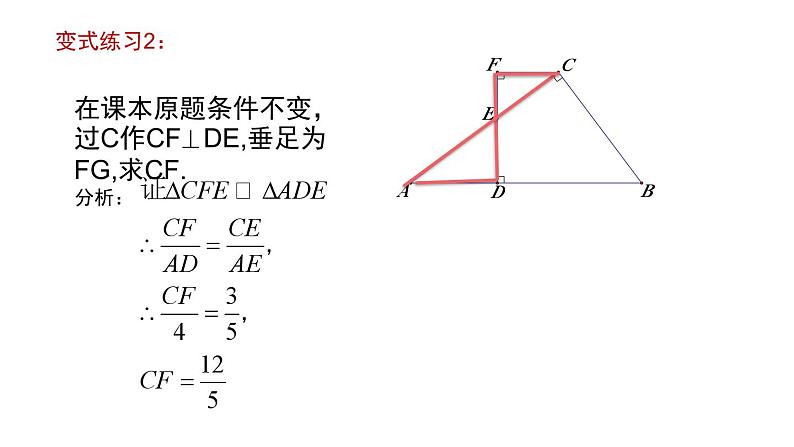
在课本原题条件不变，过C作CF DE,垂足为FG,求CF.
在课本原题条件下,将△ADE绕点A顺时针20°，连接EC,BD.说出图中两对相似三角形.
分析：△ACE∽ △ABD △AED ∽△ACB
在变式练习2条件下，过B作BG FC于G,求BG.
分析：易求CE=3,BC=6.
在创文创卫活动中，恩施市积极响应，对城区一圆形水上乐园改造升级，在其圆周上安装音乐喷泉，提升旅游服务质量.其平面结构如右图，A、B、C、D在 ⊙O 上，AB为直径，AB CD，只有BC、BE可通过地面的装饰材料尺寸估算出BC=30米，BE=18米，只借助估算两数据你能求出圆的周长吗？若能，求其周长.
（ 2021恩施中考 ） 如图，在Rt△AOB中，∠AOB=90°， 与AB相交于点 C ，与 AO 相交于点E ，连接CE ，已知∠AOC= 2∠ACE. （1）求证:AB 为 的切线； （2）若 AO=20，BO=15 ，求CE的长.
寄语：用数学的眼光看世界，用数学的思维思考世界，用数学的语言表达世界
（2022恩施）如图，P为⊙O外一点，PA、PB为⊙O的切线，切点分别为A、B，直线PO交⊙O于点D、E，交AB于点C．（1）求证：∠ADE＝∠PAE．（2）若∠ADE＝30°，求证：AE＝PE．（3）若PE＝4，CD＝6，求CE的长．
分层作业：A.完成第（1）问 B.完成第（1）（2）问 C.完成第（3）问
（2022恩施）在平面直角坐标系中，O为坐标原点，抛物线y＝﹣x2+c与y轴交于点P（0，4）．（1）直接写出抛物线的解析式．（2）如图，将抛物线y＝﹣x2+c向左平移1个单位长度，记平移后的抛物线顶点为Q，平移后的抛物线与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C．判断以B、C、Q三点为顶点的三角形是否为直角三角形，并说明理由．
（3）直线BC与抛物线y＝﹣x2+c交于M、N两点（点N在点M的右侧），请探究在x轴上是否存在点T，使得以B、N、T三点为顶点的三角形与△ABC相似，若存在，请求出点T的坐标；若不存在，请说明理由．（4）若将抛物线y＝﹣x2+c进行适当的平移，当平移后的抛物线与直线BC最多只有一个公共点时，请直接写出抛物线y＝﹣x2+c平移的最短距离并求出此时抛物线的顶点坐标．
这节课此题只解决第（3）问，（1）（2）问直接告诉答案
①△BNT∽△BCA时，则
由两点距离公式或勾股定理求
②当△NBT∽△ABC时，则