

初中数学3 反证法优秀学案及答案
展开3.反证法
学习目标:
1.了解反证法的意义及用反证法证明一个命题是真命题的一般步骤(重点);
2.学会运用反证法证明有关命题(难点).
自主学习
一、知识链接
1.在证明一些命题是真命题时,一般采用__________法.
2.在证明与图形有关的命题时,一般有哪些步骤?
答:第一步:____________________;第二步:_______________;第三步:_________________.
二、新知预习
- 除了直接证明的方法,还有_________证明的方法,_________法就是常用的间接证明方法.
2.在证明一个命题时,有时先假设______的反面是正确的;然后通过_________,推出与基本事实、已证的定理、定义或已知条件相矛盾;从而说明假设___________,进而得出原结论正确.这种证明方法叫做_______法.
合作探究
一、探究过程
探究点:反证法
操作 画出如下三角形,计算较短两边的长的平方的和,与较长边的平方,它们是否相等?
(1)1,1.5,2.4;(2)1.5,2,2.5;(3)1.5,2.5,3.
猜想 当一个三角形的三边a、b、c(a≤b≤c)有关系a2+b2≠c2时,这个三角形不是直角三角形.
问题 你会如何证明这个猜想?
【要点归纳】反证法步骤:先假设结论的反面是正确的;然后通过演绎推理,推出与基本事实、已证的定理、定义或已知条件相矛盾;从而说明假设不成立,进而得出原结论正确.
例1求证:如果两条直线都与第三条直线平行,那么这两条直线也平行.
已知: .
求证: .
证明:假设 ,则可设它们相交于点A.那么过点A 就有 条直线与直线c平行,这与“过直线外一点 ”矛盾.
∴假设不成立.
∴ .
【归纳总结】在推理论证时,要把新增的已知条件(即假设的内容)加进去,然后逐步推出与已知公理或定理之间的矛盾.
【针对训练】求证:在一个三角形中,至少有一个内角小于或等于60°.
已知: .
求证: .
证明:假设 ,即_______________________.
∴∠A+∠B+∠C>____________,这与三角形的 相矛盾.
∴假设不成立.
∴ .
例2 求证:命题“三角形中最多有一个角是直角”.
【归纳总结】若结论的反面不止一种情况,必须把各种可能情况全部列举出来,并逐一加以否定,才能肯定原结论是正确的.
二、课堂小结
![]() 反证法的意义
反证法的意义
反证法 反证法的一般步骤
用反证法证明有关命题
当堂检测
1.在证明“在△ABC中至少有一个角是锐角”时,第一步应假设( )
A.三角形至少有一个角是锐角 B.三角形中至少有两个锐角
C.三角形中没有锐角 D.三角形中三个角都是锐角
2.反证法证明命题“同旁内角不互补的两条直线不平行”时,应先假设 .
3.写出下列各结论的反面:
(1)a//b: ;
(2)a≥0: ;
(3)b是正数: ;
(4)一个三角形中最多有一个钝角: .
4.已知直线m、n是相交线,且直线l1⊥m,直线l2⊥n.求证:直线l1与l2必相交.
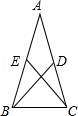
5.如图,在△ABC中,D、E分别是AC、AB上的中点,且BD≠CE,求证:AB≠AC.
参考答案
自主学习
一、知识链接
1.反证 2.画图,写出已知 写求证过程 写出结论
二、新知预习
1.间接 反证
2结论 演绎推理 基本事实 不成立 反证
合作探究
一、探究过程
探究点:
操作 解:各三角形如图①②③所示:
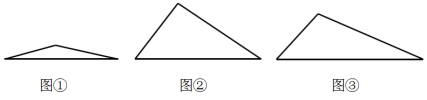
(1)12+1.52≠2.42;(2)1.52+22=2.52;(3)1.52+2.52≠32.所以(2)中相等,(1)(3)中不相等.
例1 在同一平面内,直线a∥c,b∥c 直线a∥b 直线a与直线b相交 2 有且只有一条直线与已知直线平行 直线a∥b
【针对训练】∠A,∠B,∠C是△ABC的内角 △ABC中至少有一个内角小于或等于60° △ABC中没有一个内角小于或等于60° ∠A,∠B,∠C都大于60° 180° 内角和为180° 三角形三个内角中至少有一个内角小于或等于60°
例2 证明:假设三角形中有两个角为90°,则三角形三个内角之和大于180°,这与“三角形的内角和为180°”相悖,所以假设不正确.所以三角形中最多有一个角是直角.
当堂检测
1. C 2.同旁内角不互补的两条直线平行
3.(1)直线a与直线b不平行 (2)a<0
(3)b是非正数 (4)一个三角形中最少有两个钝角
4.证明:假设直线l1与l2不相交,则两直线平行.∵l1∥l2,直线l1⊥m,直线l2⊥n.∴m∥n,这与直线m、n是相交线相矛盾.∴假设不正确,则直线l1与l2必相交.
5.解:假设AB=AC,则∠ABC=∠ACB.∵AB=AC,D、E分别是AC、AB上的中点,∴BE=CD.在△BCD和△CBE中,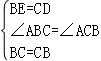 ,∴△BCD≌△CBE.∴BD=CE,这与BD≠CE相矛盾.则AB≠AC.
,∴△BCD≌△CBE.∴BD=CE,这与BD≠CE相矛盾.则AB≠AC.
数学八年级上册2 数据的收集精品导学案: 这是一份数学八年级上册2 数据的收集精品导学案,共5页。学案主要包含了知识链接,新知预习等内容,欢迎下载使用。
初中数学华师大版八年级上册3 边角边优秀导学案: 这是一份初中数学华师大版八年级上册3 边角边优秀导学案,共6页。学案主要包含了知识链接,新知预习等内容,欢迎下载使用。
数学1 命题优质学案设计: 这是一份数学1 命题优质学案设计,共4页。学案主要包含了知识链接,新知预习等内容,欢迎下载使用。













