广东省东莞中学2022-2023学年数学七年级第二学期期末统考模拟试题含答案

广东省东莞中学2022-2023学年数学七年级第二学期期末统考模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题(每小题3分,共30分)

1．若两个相似三角形的周长比为4:3，则它们的相似比为（    ）．

A．4:3 B．3:4 C．16:9 D．9:16

2．下列运算结果正确的是(　　)

A．＝﹣3 B．(﹣)2＝2 C．÷＝2 D．＝±4

3．下列长度的三条线段，能成为一个直角三角形的三边的一组是（　　）

A． B．1，2， C．2，4， D．9，16，25

4．如图所示，购买一种苹果，所付款金额（单元：元）与购买量（单位：千克）之间的函数图像由线段和射线组成，则一次购买千克这种苹果，比分五次购买，每次购买千克这种苹果可节省（  ）

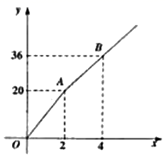
A．元 B．元 C．元 D．元

5．下列函数：①y＝2x+1 ②y＝③y＝x2﹣1 ④y＝﹣8x中，是一次函数的有（　　）

A．1个 B．2个 C．3个 D．4个

6．已知一个直角三角形的两边长分别为3和4，则第三边长为（　　）

A．5 B．7 C． D．或5

7．如图，在△ABC中，∠ABC的平分线交AC于点D，AD＝6，过点D作DE∥BC交AB于点E，若△AED的周长为16，则边AB的长为（　　）

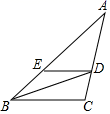
A．6 B．8 C．10 D．12

8．在□ABCD中，∠A、∠B的度数之比为5∶4，则∠C等于（    ）

A．60° B．80° C．100° D．120°

9．若分式在实数范围内有意义，则实数的取值范围是(    )

A． B． C． D．

10．已知甲.乙两组数据的平均数相等，若甲组数据的方差＝0.055，乙组数据的方差＝0.105，则（     ）

A．甲组数据比乙组数据波动大 B．乙组数据比甲组数据波动大

C．甲组数据与乙组数据的波动一样大 D．甲.乙两组数据的数据波动不能比较

二、填空题(本大题共有6小题，每小题3分，共18分)

11．如图，四边形ABCD中，若去掉一个60°的角得到一个五边形，则∠1＋∠2=_______度．

12．已知＝，＝，那么＝_____（用向量、的式子表示）

13．在 中，若是 的正比例函数，则常数 _____．

14．在矩形中, 与相交于点，,那么的度数为，__________．

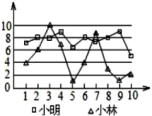
15．小林和小明练习射击，第一轮10枪打完后两人打靶的环数如图所示，根据图中的信息，成绩较稳定的是____．

16．已知一次函数的图象与直线y=﹣x+1平行，且过点（8，2），那么此一次函数的解析式为    ．

三、解下列各题(本大题共8小题，共72分)

17．（8分）在平面直角坐标系中,一次函数的图象经过点．

(1)当时,且正比例函数的图象经过点．

①若,求的取值范围；

②若一次函数的图象为,且不能围成三角形,求的值；

(2)若直线与轴交于点,且,求的数量关系．

18．（8分）某学校组织了“热爱宪法，捍卫宪法”的知识竞赛，赛后发现所有学生的成绩（总分100分）均不低于50分，为了解本次竞赛的成绩分布情况，随机抽取若干名学生的成绩作为样本进行整理，并绘制了不完整的统计图表，请你根据统计图表解答下列问题．

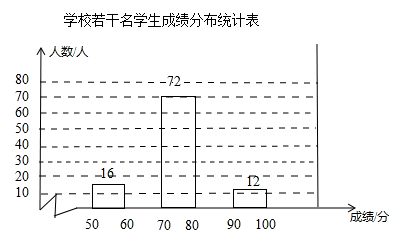
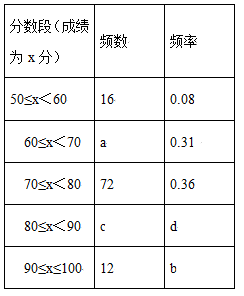
（1）此次抽样调查的样本容量是_________；

（2）写出表中的a=_____，b=______，c=________；

（3）补全学生成绩分布直方图；

（4）比赛按照分数由高到低共设置一、二、三等奖，若有25%的参赛学生能获得一等奖，则一等奖的分数线是多少？

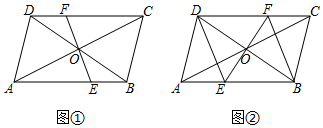
19．（8分）如图，在Rt△ABC中，∠C＝90°．

（1）求作：△ABC的一条中位线，与AB交于D点，与BC交于E点．（保留作图痕迹，不写作法）

（2）若AC＝6，AB＝10，连结CD，则DE＝_     ，CD＝_     ．

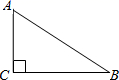
20．（8分）在▱ABCD中，对角线AC，BD相交于点O．EF过点O且与ABCD分别相交于点E，F

（1）如图①，求证：OE=OF；

（2）如图②，若EF⊥DB，垂足为O，求证：四边形BEDF是菱形．

21．（8分）我国南宋时期数学家秦九昭及古希腊的几何学家海伦对于问题：“已知三角形的三边，如何求三角形的面积”进行了研究，并得到了海伦—秦九昭公式：如果一个三角形的三条边分别为，记，那么三角形的面积为，请用此公式求解：在中，，，，求的面积.

22．（10分）（1）如图1，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开；再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN，MN．请你观察图1，猜想∠MBN的度数是多少，并证明你的结论；
（2）将图1中的三角形纸片BMN剪下，如图2，折叠该纸片，猜测MN与BM的数量关系，无需证明．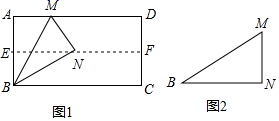
 

23．（10分）为积极响应新旧功能转换，提高公司经济效益，某科技公司近期研发出一种新型高科技设备，每台设备成本价为30万元，经过市场调研发现，每台售价为35万元时，年销售量为550台；每台售价为40万元时，年销售量为500台.假定该设备的年销售量（单位：台）和销售单价（单位：万元）成一次函数关系.

（1）求年销售量与销售单价的函数关系式；

（2）根据相关规定，此设备的销售单价不得高于60万元，如果该公司想获得8000万元的年利润，则该设备的销售单价应是多少万元？

24．（12分）某服装店准备购进甲、乙两种服装出售，甲种每件售价120元，乙种每件售价90元．每件甲服装的进价比乙服装的进价贵20元，购进3件甲服装的费用和购进4件乙服装的费用相等，现计划购进两种服装共100件，其中甲种服装不少于65件．

（1）甲种服装进价为　　元/件，乙种服装进价为　　元/件；

（2）若购进这100件服装的费用不得超过7500元．

①求甲种服装最多购进多少件？

②该服装店对甲种服装每件降价元，乙种服装价格不变，如果这100件服装都可售完，那么该服装店如何进货才能获得最大利润？

参考答案

一、选择题(每小题3分,共30分)

1、A

2、B

3、B

4、B

5、B

6、D

7、C

8、C

9、D

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、240°

12、.

13、2

14、

15、小明

16、y=－x+1

三、解下列各题(本大题共8小题，共72分)

17、（1）①；②的值为或1或；（2）.

18、（1）200；（2）62，0.06，38；（3）见解析；（4）1

19、（1）作图见解析；（2）3，1 .

20、（1）证明见解析；（2）证明见解析.

21、

22、（1）30º，见解析．（2）

23、（1）年销售量与销售单价的函数关系式为；（2）该设备的销售单价应是50万元/台.

24、（1）80；60；（2）①甲种服装最多购进75件；②当时，购进甲种服装75件，乙种服装25件；当时，所有进货方案获利相同；当时，购进甲种服装65件，乙种服装35件．