


山西省朔州市右玉县2022-2023学年数学七年级第二学期期末综合测试模拟试题含答案
展开山西省朔州市右玉县2022-2023学年数学七年级第二学期期末综合测试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
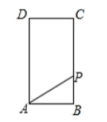
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。
4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.点![]() 到
到![]() 轴的距离为( )
轴的距离为( )
A.3 B.4 C.5 D.![]()
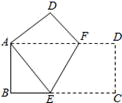
2.如图,将一个边长分别为8,16的矩形纸片ABCD沿EF折叠,使C点与A点重合,则EF与AF的比值为( )
A.4 ![]() B.
B.![]() C.2 D.
C.2 D.![]()
3.一个正多边形的每个内角的度数都等于相邻外角的2倍,则该正多边形的边数是( )
A.3 B.4 C.6 D.12
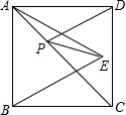
4.如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一动点P,则PD+PE的和最小值为( )
A.![]() B.4 C.3 D.
B.4 C.3 D.![]()
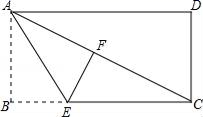
5.已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )
A.3 B.4 C.5 D.6
6.如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 向终点
向终点![]() 匀速运动.设点
匀速运动.设点![]() 走过的路程为
走过的路程为![]() ,
,![]() 的面积为
的面积为![]() ,能正确反映
,能正确反映![]() 与
与![]() 之间函数关系的图象是( )
之间函数关系的图象是( )
A.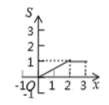 B.
B.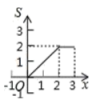
C.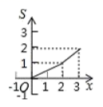 D.
D.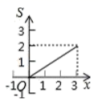
7.下列各式从左到右的变形中,是因式分解的是( )
A.(a 3)(a 3) a2 9 B.a2 2a 3 a(a 2 ![]() )
)
C.a 2 4a 5 (a 4) 5 D.a2b2 (a b)(a b)
8.下列四组线段中,不能作为直角三角形三条边的是( )
A.3cm,4cm,5cm B.2cm,2cm,2![]() cm C.2cm,5cm,6cm D.5cm,12cm,13cm
cm C.2cm,5cm,6cm D.5cm,12cm,13cm
9.下列给出的四个点中,在函数y=2x﹣3图象上的是( )
A.(1,﹣1) B.(0,﹣2) C.(2,﹣1) D.(﹣1,6)
10.去年某市7月1日到7日的每一天最高气温变化如折线图所示,则关于这组数据的描述正确的是( )
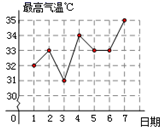
A.最低温度是32℃ B.众数是35℃ C.中位数是34℃ D.平均数是33℃
二、填空题(本大题共有6小题,每小题3分,共18分)
11.如图,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,若
的中点,若![]() ,则线段
,则线段![]() 的长是__________.
的长是__________.
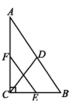
12.如图,长方体的底面边长分别为1cm 和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要_____cm.
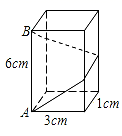
13.菱形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边长作正方形
为边长作正方形![]() ,则点
,则点![]() 到
到![]() 的距离为_________.
的距离为_________.
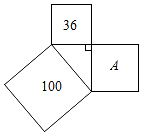
14.如图,三个正方形中,其中两个正方形的面积分别是100,36,则字母A所代表的正方形的边长是_____.
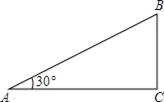
15.如图所示,小明从坡角为30°的斜坡的山底(A)到山顶(B)共走了100米,则山坡的高度BC为_____米.
16.化简: ![]() 的结果是_____.
的结果是_____.
三、解下列各题(本大题共8小题,共72分)
17.(8分)已知四边形![]() 中,
中,![]() ,垂足为点
,垂足为点![]() ,
,![]() .
.
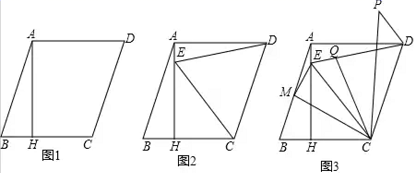
(1)如图1,求证:![]() ;
;
(2)如图2,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,
,![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,如图3,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 为
为![]() 的中点,分别连接
的中点,分别连接![]() ,
,![]() ,
,![]() +
+![]() =
=![]() =
=![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
18.(8分)某商场统计了每个营业员在某月的销售额,绘制了如下的条形统计图以及不完整的扇形统计图:
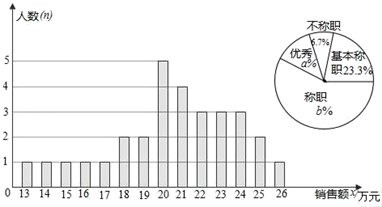
解答下列问题:(1)设营业员的月销售额为x(单位:万元),商场规定:当x<15时为不称职,当15≤x<20时,为基本称职,当20≤x<25为称职,当x≥25时为优秀.则扇形统计图中的a=_____,b=_____.
(2)所有营业员月销售额的中位数和众数分别是多少?
(3)为了调动营业员的积极性,决定制定一个月销售额奖励标准,凡到达或超过这个标准的营业员将受到奖励.如果要使得营业员的半数左右能获奖,奖励标准应定为多少万元?并简述其理由.
19.(8分)直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点,过点
两点,过点![]() 的直线交
的直线交![]() 轴负半轴于
轴负半轴于![]() ,且
,且![]() .
.
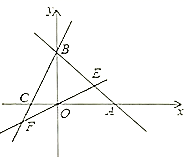
![]() 求点
求点![]() 坐标.
坐标.
![]() 求直线
求直线![]() 的解析式.
的解析式.
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
20.(8分)已知x=![]() +1 , y=
+1 , y=![]() -1 , 求x2+xy+y2的值.
-1 , 求x2+xy+y2的值.
21.(8分)我们可用![]() 表示以
表示以![]() 为自变量的函数,如一次函数
为自变量的函数,如一次函数![]() ,可表示为
,可表示为![]() ,且
,且![]() ,
,![]() ,定义:若存在实数
,定义:若存在实数![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点,例如:
的不动点,例如:![]() ,令
,令![]() ,得
,得![]() ,那么
,那么![]() 的不动点是1.
的不动点是1.
(1)已知函数![]() ,求
,求![]() 的不动点.
的不动点.
(2)函数![]() (
(![]() 是常数)的图象上存在不动点吗?若存在,请求出不动点;若不存在,请说明理由;
是常数)的图象上存在不动点吗?若存在,请求出不动点;若不存在,请说明理由;
(3)已知函数![]() (
(![]() ),当
),当![]() 时,若一次函数
时,若一次函数![]() 与二次函数
与二次函数![]() 的交点为
的交点为![]() ,即
,即![]() 两点的横坐标是函数
两点的横坐标是函数![]() 的不动点,且
的不动点,且![]() 两点关于直线
两点关于直线![]() 对称,求
对称,求![]() 的取值范围.
的取值范围.
22.(10分)如图,直角坐标系xOy中,一次函数y=kx+b的图象l1分别与x轴,y轴交于A(15,0),B两点,正比例函数y=![]() x的图象l2与l1交于点C(m,3).
x的图象l2与l1交于点C(m,3).
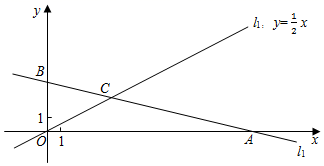
(1)求m的值及l1所对应的一次函数表达式;
(2)根据图象,请直接写出在第一象限内,当一次函数y=kx+b的值大于正比例函数y=![]() x的值时,自变量x的取值范围.
x的值时,自变量x的取值范围.
23.(10分)小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50min才乘上缆车,缆车的平均速度为180m/min.设小亮出发xmin后行走的路程为ym.图中的折线表示小亮在整个行走过程中y与x的函数关系.
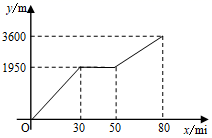
(1)小亮行走的总路程是______m,他途中休息了______min,休息后继续行走的速度为______m/min;
(2)当![]() 时,求y与x的函数关系式;
时,求y与x的函数关系式;
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
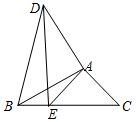
24.(12分)如图,将△ABC绕点A顺时针旋转得到△ADE(点B,C的对应点分别是D,E),当点E在BC边上时,连接BD,若∠ABC=30°,∠BDE=10°,求∠EAC.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、B
3、C
4、B
5、C
6、A
7、D
8、C
9、A
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1.
12、1
13、5+![]() 或5-
或5-![]() .
.
14、1
15、1
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)见解析;(2)见解析;(3)![]()
18、(1)10;60;(2)中位数为21、众数为20;(3)奖励标准应定为21万元,理由见解析
19、(1)(0,6);(2)y=3x+6;(3)证明见详解
20、7
21、(1![]() 的不动点为0和2;(2)①
的不动点为0和2;(2)①![]() 时,有唯一的不动点
时,有唯一的不动点![]() ②
②![]() 时,有无数个不动点③
时,有无数个不动点③![]() 时,没有不动点;(3)
时,没有不动点;(3)![]() 的取值范围是
的取值范围是![]()
22、(1)m=1,l1的解析式为y=-![]() x+5;(2)自变量x的取值范围是0<x<1.
x+5;(2)自变量x的取值范围是0<x<1.
23、(1)3600,20,1;(2)y=1x-2;(3)当小颖到达缆车终点时,小亮离缆车终点的路程是1100m.
24、∠EAC=100°.
山西省朔州市右玉县2023-2024学年九上数学期末统考模拟试题含答案: 这是一份山西省朔州市右玉县2023-2024学年九上数学期末统考模拟试题含答案,共10页。
山西省朔州市右玉县2022-2023学年七年级上学期期末模拟测试数学试卷(含解析): 这是一份山西省朔州市右玉县2022-2023学年七年级上学期期末模拟测试数学试卷(含解析),共13页。试卷主要包含了选择题等内容,欢迎下载使用。
山西省朔州市右玉县2022-2023学年八年级上学期期末模拟测试数学试卷(含解析): 这是一份山西省朔州市右玉县2022-2023学年八年级上学期期末模拟测试数学试卷(含解析),共16页。试卷主要包含了选择题等内容,欢迎下载使用。












